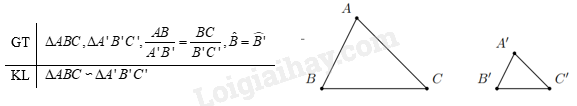Trường hợp đồng dạng thứ hai (c.g.c)Trường hợp đồng dạng thứ hai là gì? 1. Lý thuyết Định lí Trường hợp đồng dạng thứ hai (cạnh – góc – cạnh): Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng. 2. Ví dụ minh họa
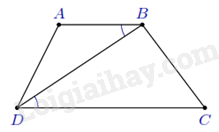
Ví dụ 1: Cho hình thang ABCD (AB∥CD). Biết AB=9 cm, BD=12 cm và DC=16 cm. Chứng minh ΔABD∽ΔBDC. Lời giải.
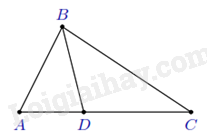
Ta có ^ABD=^BDC và BABD=DBDC=34. ⇒ΔABD∽ΔBDC (c.g.c). Ví dụ 2: Cho tam giác ABC có AB=4 cm, AC=8 cm. Trên cạnh AC lấy D sao cho AD=2 cm. Chứng minh a) ^ABD=^ACB; b) BC=2BD. Lời giải.
a) Xét ΔABD và ΔACB có ˆA chung, ADAB=ABAC=12 ⇒ΔABD∽ΔACB (c.g.c), suy ra ^ABD=^ACB. b) Từ câu a), ta có BCBD=ACAB=2⇒ đpcm.  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|
