Định lí Pytagore và ứng dụngĐịnh lí Pythagore là gì? Định lí Pythagore đảo là gì? Ta có thể sử dụng định lí Pythagore để giải quyết các vấn đề nào? 1. Lý thuyết - Định lí Pythagore: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
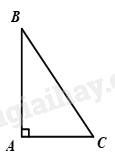
\(\Delta ABC\) vuông tại \(A\) \( \Rightarrow B{C^2} = A{B^2} + A{C^2}\) . - Định lí Pythagore đảo: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông. \(\Delta ABC\) có\(\,B{C^2} = A{B^2} + A{C^2} \Rightarrow \widehat {BAC} = {90^0}\) - Ứng dụng của định lí Pythagore + Tính độ dài đoạn thẳng
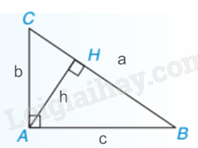
Nhận xét: Nếu tam giác vuông ABC tại A có đường cao AH = h, các cạnh BC = a, AC = b, AB = c thì h.a = b.c. + Chứng minh tính chất hình học
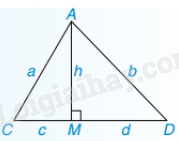
Chú ý: AM là đường cao, AC, AD là đường xiên thì đoạn thẳng MC là hình chiếu của đường xiên AC và MD là hình chiếu của đường xiên AD. 2. Ví dụ minh họa Ví dụ 1: Cho tam giác \(ABC\) vuông tại \(A\), có \(AB = 6\)cm, \(AC = 8\)cm. a) Tính độ dài cạnh \(BC\). b) Kẻ \(AH\) vuông góc với \(BC\) tại \(H\). Biết \(AH = 4,8\) cm. Tính \(BH,CH\). Lời giải a) \(\Delta ABC\) vuông tại \(A\) nên theo định lí Pythagore ta có : \(B{C^2} = A{B^2} + A{C^2} \Rightarrow B{C^2} = {6^2} + {8^2} = 100 \Rightarrow BC = \sqrt {100} = 10{\rm{ cm}}.\) \(\Delta ABH\) vuông tại \(H\) nên theo định lí Pythagore ta có : \(\begin{array}{l}A{B^2} = A{H^2} + B{H^2} \Rightarrow B{H^2} = A{B^2} - A{H^2}\\ \Rightarrow B{H^2} = {6^2} - {(4,8)^2} = 12,96 \Rightarrow BH = \sqrt {12,96} = 3,6{\rm{ cm}}.\end{array}\) Từ đó tính được \(HC = BC - BH = 10 - 3,6 = 6,4\) cm. Ví dụ 2: Cho tam giác \(ABC\) vuông tại \(A\), có \(AB = 6\) cm, \(AC = 8\) cm. \(D\) là một điểm sao cho \(BD = 16\) cm, \(CD = 24\) cm. Chứng minh \(\Delta CBD\) không thể là tam giác vuông. Lời giải Tam giác \(ABC\) vuông tại \(A\) nên theo định lý Pythagore ta có \(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100 \Rightarrow BC = \sqrt {100} = 10{\rm{ cm}}\) Tam giác \(CBD\) không thể là tam giác vuông vì \({24^2} \ne {10^2} + {16^2}\).
|