Lý thuyết diện tích hình tam giácCho hai hình tam giác bằng nhau (xem hình vẽ). Diện tích hình tam giác Quy tắc: Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho $2$. 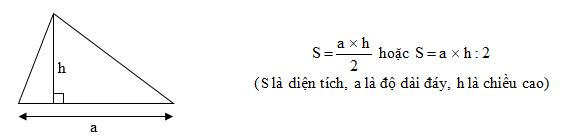 Chú ý: Muốn tính diện tích tam giác vuông ta lấy độ dài hai cạnh góc vuông nhân với nhau (cùng một đơn vị đo) rồi chia cho \(2\). Ví dụ 1: Tính diện tích hình tam giác có độ dài đáy là \(13cm\) và chiều cao là \(8cm\). Cách giải: Diện tích hình tam giác đó là: \(13 \times 8:2 = 52(c{m^2})\) Đáp số: \(52c{m^2}\). Ví dụ 2: Tính diện tích hình tam giác có độ dài đáy là \(2m\) và chiều cao là \(15dm\). Cách giải: Đổi \(2m = 20dm\) Diện tích hình tam giác đó là: \(20 \times 15:2 = 150(d{m^2})\) Đáp số: \(150c{m^2}\). 3) Một số dạng bài tập Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao Phương pháp: Áp dụng công thức: \(S = \dfrac{{a\,\, \times \,\,h}}{2}\) hoặc \(S = a\,\, \times \,\,h:2\) (\(S\) là diện tích, \(a\) là độ dài đáy, \(h\) là chiều cao) Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao Phương pháp: Từ công thức tính diện tích \(S = \dfrac{{a\,\, \times \,\,h}}{2}\) hoặc \(S = a\,\, \times \,\,h:2\), ta có công thức tính độ dài đáy như sau: \(a = \dfrac{{S \times 2}}{h}\) hoặc \(a = S \times 2:h\). Dạng 3: Tính chiều cao khi biết diện tích và độ dài đáy Phương pháp: Từ công thức tính diện tích \(S = \dfrac{{a\,\, \times \,\,h}}{2}\) hoặc \(S = a\,\, \times \,\,h:2\), ta có công thức tính chiều cao như sau: \(h = \dfrac{{S \times 2}}{a}\) hoặc \(h = S \times 2:a\). Dạng 4: Toán có lời văn Phương pháp: Đọc kĩ đề bài, xác định dạng toán trong bài rồi giải bài toán đó. |













