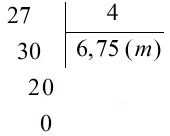Toán lớp 5 trang 68 Chia một số tự nhiên cho một số tự nhiên mà thương tìm được là một số thập phân

Bài 1

Đặt tính rồi tính:

a) \(12 : 5\)                                 b) \(15 : 8\)

    \(23 : 4\)                                     \(75 : 12\)

    \(882 : 36\)                                 \(81 : 4\)

Phương pháp giải:

Khi chia một số tự nhiên cho một số tự nhiên mà còn dư, ta tiếp tục chia như sau:

- Viết dấu phẩy vào bên phải số thương.

- Viết thêm vào bên phải số dư một chữ số \(0\) rồi chia tiếp.

- Nếu còn dư nữa, ta lại viết thêm bên phải số dư mới một chữ số \(0\) rồi tiếp tục chia, và có thể cứ làm như thế mãi.

Lời giải chi tiết:

Bài 2

May \(25\) bộ quần áo như nhau hết \(70m\) vải. Hỏi may \(6\) bộ quần áo như thế hết bao nhiêu mét vải?

Phương pháp giải:

- Số vải may \(1\) bộ quần áo \(=\) số vải may \(25\) bộ quần áo \(: 25\).

- Số vải may 6 bộ quần áo \(=\) số vải may 1 bộ quần áo \(\times\,6\).

Lời giải chi tiết:

Tóm tắt:

\(25\) bộ: \(70m\)

\(6\) bộ:   \(...\; m\;?\)

Giải

May \(1\) bộ quần áo hết số mét vải là:

               \(70 : 25 = 2,8\;(m)\)

May \(6\) bộ quần áo hết số mét vải là: 

               \(2,8 × 6 = 16,8\;(m)\)

                                    Đáp số: \(16,8m.\)

Bài 3

Viết các phân số sau dưới dạng số thập phân:

\(\dfrac{2}{5}\);         \(\dfrac{3}{4}\);         \(\dfrac{18}{5}\).

Phương pháp giải:

\( \dfrac{a}{b} = a : b\). Do đó để viết phân số \( \dfrac{a}{b}\) dưới dạng số thập phân ta thực hiện phép tính chia \( a : b\).

Lời giải chi tiết:

Vậy: \(\dfrac{2}{5}= 0 ,4\) ;         \(\dfrac{3}{4} = 0,75\);          \(\dfrac{18}{5} = 3,6\). 

Lý thuyết

a) Ví dụ 1: Một cái sân hình vuông có chu vi 27m. Hỏi cạnh của sân dài bao nhiêu mét?

Ta phải thực hiện phép chia:       \(27 : 4 = \; ?\)

Thông thường ta đặt tính rồi làm như sau:

•  \(27\) chia \(4\) được \(6\), viết \(6\);

    \(6\) nhân \(4\) được \(24\), \(27\) trừ \(24\) được \(3\), viết \(3\);

•  Để chia tiếp, ta viết dấu phẩy vào bên phải \(6\) và viết thêm chữ số \(0\) vào bên phải \(3\) được \(30\).

   \(30\) chia \(4\) được \(7\), viết \(7\); 

   \(7\) nhân \(4\) bằng \(28\); \(30\) trừ \(28\) bằng \(2\), viết \(2\).

•  Viết thêm chữ số \(0\) vào bên phải \(2\) được \(20\); \(20\) chia \(4\) được \(5\) viết \(5\);

    \(5\) nhân \(4\) bằng \(20\); \(20\) trừ \(20\) bằng \(0\) viết \(0\).

Vậy:     \( 27 : 4 = 6,75 \;(m)\).

b) Ví dụ 2:      \(43: 52 = \;?\)

Phép chia này có số bị chia \(43\) bé hơn số chia \(52\), ta có thể làm như sau:

• Chuyển \(43\) thành \(43,0\)

• Đặt tính rồi tính như phép chia \(43,0 : 52\) (chia số thập phân cho số tự nhiên).

Khi chia một số tự nhiên cho một số tự nhiên mà còn dư, ta tiếp tục chia như sau:

- Viết dấu phẩy vào bên phải số thương.

- Viết thêm vào bên phải số dư một chữ số 0 rồi chia tiếp.

- Nếu còn dư nữa, ta lại viết thêm bên phải số dư mới một chữ số 0 rồi tiếp tục chia, và có thể cứ làm như thế mãi.