Giải Toán lớp 5 trang 3 SGK - Ôn tập: Khái niệm về phân số

Bài 1

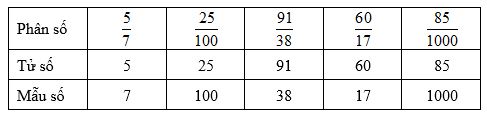
a) Đọc các phân số:

\(\dfrac {5}{7}\);  \(\dfrac {25}{100}\);  \(\dfrac {91}{38}\);  \(\dfrac {60}{17}\);   \(\dfrac {85}{1000}\).

b) Nêu tử số và mẫu số của từng phân số trên.

Phương pháp giải:

a) Cách đọc phân số: đọc tử số rồi đọc "phần" sau đó đọc mẫu số.

b) Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới gạch ngang.

Lời giải chi tiết:

a) \(\dfrac {5}{7}\): năm phần bảy;

    \(\dfrac {25}{100}\): hai mươi lăm phần một trăm (hoặc hai mươi lăm phần trăm);

    \(\dfrac {91}{38}\): chín mươi mốt phần ba mươi tám;

    \(\dfrac {60}{17}\): sáu mươi phần mười bảy;

    \(\dfrac {85}{1000}\): tám mươi lăm phần một nghìn (hoặc tám mươi lăm phần nghìn).

b) 

Bài 2

Viết các thương sau dưới dạng phân số:  \(3 : 5; \quad 75 : 100; \quad 9 : 17\).

Phương pháp giải:

Thương của phép chia số tự nhiên cho số tự nhiên (khác 0) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.

Lời giải chi tiết:

\(3 : 5 = \dfrac {3}{5}\) ;       \(75 : 100 =\dfrac {75}{100}\);        \(9 : 17 = \dfrac {9}{17}\).

Bài 3

Viết các số tự nhiên dưới dạng phân số có mẫu số là \(1\):

                      \(32\);     \(105\);     \(1000\).

Phương pháp giải:

Mọi số tự nhiên có thể viết thành một phân số có tử số là số tự nhiên đó và mẫu số là \(1\).

Lời giải chi tiết:

\(32 =\dfrac {32}{1}\);     \(105 = \dfrac {105}{1}\);      \( 1000 = \dfrac {1000}{1}\).

Bài 4

Viết số thích hợp vào ô trống:

a)  \(1 = \dfrac {6}{\square }\);                            b) \( 0 = \dfrac {\square }{5}\).

Phương pháp giải:

Số \(1\) có thể viết thành phân số có tử số và mẫu số bằng nhau và khác \(0\).

Số \(0\) có thể viết thành phân số có tử số là \(0\) và mẫu số khấc \(0\).

Lời giải chi tiết:

a)  \(1 = \dfrac {6}{6 }\);                               b) \( 0 = \dfrac {0}{5}\).

Lý thuyết

>> Xem chi tiết: Lý thuyết ôn tập: Khái niệm về phân số