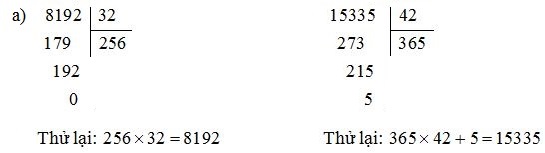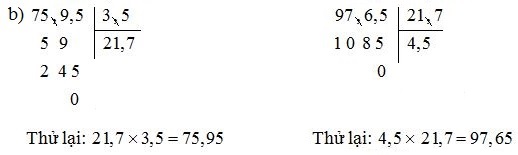Toán lớp 5 trang 163, 164 Phép chia

Bài 1

Tính rồi thử lại (theo mẫu):

a) 8192 : 32 ;                         15335 : 42.

b) 75,95 : 3,5 ;                        97,65 : 21,7 (thương là số thập phân)

Chú ý: Phép chia hết: a : b = c, ta có a = c × b (b khác 0)

Phép chia có dư: a : b = c (dư r), ta có a = c × b + r (0 < r < b).

Phương pháp giải:

Đặt tính rồi tính theo các quy tắc đã học. 

Lời giải chi tiết:

Bài 2

Tính: 

a) \(\dfrac{3}{10} : \dfrac{2}{5}\) ;                                              b) \(\dfrac{4}{7} : \dfrac{3}{11}\).

Phương pháp giải:

Để chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược:

                  \( \dfrac{a}{b} :\dfrac{c}{d} = \dfrac{a}{b} \times \dfrac{d}{c}\).

Lời giải chi tiết:

a) \(\dfrac{3}{10} : \dfrac{2}{5} = \dfrac{3}{10} \times \dfrac{5}{2} = \dfrac{15}{20} = \dfrac{3}{4}\) ;

b)  \(\dfrac{4}{7} : \dfrac{3}{11} = \dfrac{4}{7} \times \dfrac{11}{3} = \dfrac{44}{21}\).

Bài 3

Tính nhẩm:

a) \(25 : 0,1\)                                \(25 × 10\)

    \(48 : 0,01\)                               \(48 × 100\)

    \(95 : 0,1\)                                 \(72 : 0,01\)

b) \(11 : 0,25\)                              \(11 × 4\)

    \(32 : 0,5\)                                \(32 × 2\)

    \(75 : 0,5\)                                \(125 : 0,25\)

Phương pháp giải:

- Muốn chia một số tự nhiên cho 0,1; 0,01; 0,001; ... ta chỉ việc thêm vào bên phải số đó một, hai, ba, ... chữ số 0.

- Muốn nhân một số tự nhiên với 10; 100; 1000;  ... ta chỉ việc thêm vào bên phải số đó một, hai, ba, ... chữ số 0.

- Muốn chia một số cho 0,25 ta chỉ việc nhân số đó với 4.

-  Muốn chia một số cho 0,5 ta chỉ việc nhân số đó với 2.

Lời giải chi tiết:

a)  \(25 : 0,1  = 250\)                                \(25 × 10 = 250\)

    \(48 : 0,01 = 4800\)                                \(48 × 100 = 4800\)

    \(95 : 0,1 = 950\)                                   \(72:0,01=7200\)

b) \(11 : 0,25 = 11 × 4 = 44\)

    \(11 × 4 = 44\)

    \(32 : 0,5 =  32 × 2 = 64\)

    \(32 × 2 = 64\)

   \(75 : 0,5 = 75 × 2 = 150\)

   \(125 : 0,25 =125 × 4 = 500.\)

Bài 4

Tính bằng hai cách:

a) \(\dfrac{7}{11}: \dfrac{3}{5} + \dfrac{4}{11} : \dfrac{3}{5}\) ;                     

b) \((6,24 + 1,26) : 0,75\).

Phương pháp giải:

Áp dụng công thức: \( (a + b) : c = a : c + b: c\)

Lời giải chi tiết:

a) Cách 1: 

\(\dfrac{7}{11}\) \(:\dfrac{3}{5}\) \(+ \dfrac{4}{11}\) \(: \dfrac{3}{5}\)

\(= \dfrac{7}{11}  \times \dfrac{5}{3}+ \dfrac{4}{11}  \times \dfrac{5}{3}\)

\(= \dfrac{35}{33}+ \dfrac{20}{33}\) 

\(=\dfrac{55}{33}= \dfrac{5}{3}\)

Cách 2: 

\(\dfrac{7}{11}: \dfrac{3}{5}+ \dfrac{4}{11} :\dfrac{3}{5}\) 

\(= \left( \dfrac{7}{11}  + \dfrac{4}{11} \right )  : \dfrac{3}{5}\) 

\(= \dfrac{11}{11} : \dfrac{3}{5}\) 

 \(= 1: \dfrac{3}{5} = \dfrac{5}{3}\) 

b) Cách 1 : 

 \( (6,24 + 1,26) : 0,75\)

\(= 7,5 : 0,75 = 10 \)

Cách 2: 

\( (6,24 + 1,26) : 0,75  \)

\(=  6,24 : 0,75 + 1,26 : 0,75 \)

\(= 8,32 + 1,68 = 10 \).

Lý thuyết

>> Xem chi tiết: Lý thuyết phép chia