Đề kiểm tra học kì 1 Toán 5 - Đề số 31Đáp án và lời giải chi tiết Đề số 26 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán lớp 5
Lựa chọn câu để xem lời giải nhanh hơn
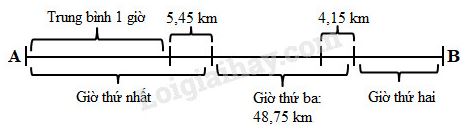
Đề bài Câu 1. Đúng ghi Đ, sai ghi S: Tìm \(x\), biết: a) \(7,3 \times x + x \times 2,7 - x = 405\) \(x = 40\) ☐ \(x = 40,5\) ☐ \(x = 45\) ☐ b) \(\overline {x,x} + x \times 8,9 = 60\) \(x = 4\) ☐ \(x = 5\) ☐ \(x = 6\) ☐ Câu 2. Đúng ghi Đ, sai ghi S: A. Thực hiện phép tính khi đổi tên đơn vị \(3180\) mm = ......... m a) \(0,001m \times 3180 = 3,180m\) ☐ b) \(3180mm \times 0,001 = 3,180m\) ☐ B. Thực hiện phép tính khi đổi tên đơn vị \(1500\) m2 = .......... ha a) \(1500{m^2} \times 0,0001 = 0,15ha\) ☐ b \(0,0001ha \times 1500 = 0,15ha\) ☐ Câu 3. Đúng ghi Đ, sai ghi S: a) \(25 + 2,18 \times 5\) \( = 2,18 + 25 \times 5\) \( = 2,18 + 125\) \( = 127,18\) ☐ b) \(25 + 2,18 \times 5\) \( = 27,18 \times 5\) \( = 135,90\) ☐ c) \(25 + 2,18 \times 5\) \( = 25 + 10,90\) \( = 35,9\) ☐ Câu 4. Khoanh vào chữ đặt trước câu trả lời đúng: Có 24 chai đựng dầu hỏa, mỗi chai chứa 0,75l dầu. Mỗi lít dầu hỏa nằng 0,76kg. Mỗi vỏ chai nặng 0,25kg. Hỏi 24 chai dầu hỏa cân nặng bao nhiêu ki-lô-gam? A. 18kg B. 19,68kg C. 20,4kg Câu 5. Tính bằng cách thuận tiện nhất: a) \(2 \times 4 \times 8 \times 0,5 \times 0,125\)\( \times \left( {0,4321 + 0,5679} \right)\) b) \(3,7 \times 3,8 + 8,3 \times 3,7\)\( - 0,4 \times 3,7 \times 5\) Câu 6. Tìm \(x\) và số thập phân \(\overline {a,bc} \) biết : \(\overline {a,bc} \times \overline {xx} = 77,33\) Câu 7. Một ô tô đi từ A đến B hết 3 giờ. Giờ thứ nhất đi nhiều hơn mức trung bình của cả 3 giờ là 5,45km. Giờ thứ hai đi ít hơn mức trung bình của cả 3 giờ là 4,15km. Giờ thứ ba đi được 48,75km. Hỏi quãng đường AB dài bao nhiêu ki-lô-mét? Lời giải Câu 1. Phương pháp: - Áp dụng tính chất nhân một số với một tổng hoặc nhân một số với một hiệu: \(a\times (b+c) = a \times b + a\times c\) ; \(a\times (b-c) = a \times b - a\times c\) - Áp dụng quy tắc: Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết. Cách giải: a) \(7,3 \times x + x \times 2,7 - x = 405\) \(x \times 7,3 + x \times 2,7 - x \times 1 = 405\) \(x \times (7,3 +2,7-1) =405\) \(x \times 9 =405\) \(x=405 : 9\) \(x=45\) Vậy kết quả lần lượt là: S; S; Đ. b) \(\overline {x,x} + x \times 8,9 = 60\) \(x \times 1,1 + x \times 8,9 = 60\) \(x \times (1,1 + 8,9) = 60\) \(x \times 10 = 60\) \(x =60:10\) \(x=6\) Vậy kết quả lần lượt là: S; S; Đ. Câu 2. Phương pháp: Dựa vào cách chuyển đổi các đơn vị đo: +) \(1m=1000mm\), hay \(1mm = \dfrac{1}{1000}m = 0,001m\). +) \(1ha=10000m^2\), hay \(1m^2 = \dfrac{1}{10000}ha = 0,0001ha\). Cách giải: A. Phép tính khi đổi tên đơn vị \(3180mm = ... m\) là: \(0,001m \times 3180 = 3,180m\) Vậy kết quả lần lượt là: a) Đ ; b) S. B. Phép tính khi đổi tên đơn vị \(1500m^2 = ...ha\) là: \(0,0001ha \times 1500 = 0,15ha\) Vậy kết quả lần lượt là: a) S ; b) Đ. Câu 3. Phương pháp: Biểu thức có phép nhân và phép cộng thì ta thực hiện phép nhân trước, thực hiện phép cộng sau. Cách giải: \(25 + 2,18 \times 5\) \( = 25 + 10,90\) \( = 35,9\) Vậy kết quả lần lượt là: a) S; b) S; c) Đ. Câu 4. Phương pháp: - Tính số lít dầu hỏa có trong \(24\) chai \(=\) số lít dầu hỏa có trong \(1\) chai \(\times 24\). - Tính cân nặng của lượng dầu hỏa có trong \(24\) chai \(=\) cân nặng của \(1\) lít dầu hỏa \(\times\) số lít dầu hỏa có trong \(24\) chai. - Tính cân nặng của \(24\) vỏ chai \(=\) cân nặng của \(1\) vỏ chai \(\times 24\). - Tính cân nặng của \(24\) chai đựng đầy dầu hỏa \(=\) cân nặng của lượng dầu hỏa có trong \(24\) chai \(+\) cân nặng của \(24\) vỏ chai. Cách giải: Số lít dầu hỏa trong \(24\) chai là: \(0,75 \times 24 = 18\) (lít) \(18\) lít dầu hỏa nặng số ki-lô-gam là : \(0,76 \times 18 = 13,68\;(kg)\) \(24\) vỏ chai nặng số ki-lô-gam là: \(0,25 \times 24 = 6\;(kg)\) \(24\) chai dầu hỏa nặng số ki-lô-gam là : \(13,68 + 6 =19,68\;(kg)\) Đáp số: \(19,68 kg.\) Lưu ý: Có thể tính cân nặng của \(1\) chai đầy dầu hỏa bằng cách tính tổng cân nặng của \(0,75\) lít dầu hỏa và cân nặng của \(1\) vỏ chai. Sau đó để tính cân nặng của \(24\) chai đựng đầy dầu hỏa ta lấy cân nặng của \(1\) chai đầy dầu hỏa nhân với \(24\). Chọn B. Câu 5. Phương pháp: - Áp dụng tính chất giao hoán và kết hợp của phép nhân để nhóm các số có tích là số tự nhiên lại với nhau. - Áp dụng tính chất nhân một số với một tổng hoặc nhân một số với một hiệu: \(a\times (b+c) = a \times b + a\times c\) ; \(a\times (b-c) = a \times b - a\times c\) Cách giải: a) \(2 \times 4 \times 8 \times 0,5 \times 0,125\)\( \times \left( {0,4321 + 0,5679} \right)\) \( = \left( {2 \times 0,5} \right) \times \left( {4 \times 0,25} \right) \)\(\times \left( {8 \times 0,125} \right) \times \left( {0,4321 + 0,5679} \right)\) \( = 1 \times 1 \times 1 \times 1\) \( = 1\) b) \(3,7 \times 3,8 + 8,3 \times 3,7 - 0,4 \times 3,7 \times 5\) \( = 3,7 \times 3,8 + 8,3 \times 3,7 \)\(- \;0,4 \times 5 \times 3,7\) \( = 3,7 \times 3,8 + 8,3 \times 3,7 - 2 \times 3,7\) \( = 3,7 \times \left( {3,8 + 8,3 - 2} \right)\) \( = 3,7 \times 10,1\) \( = 37,37\) Câu 6. Phương pháp: Áp dụng các tính chất: +) Nếu \(a=b\) và \(c\) khác \(0\) thì \(a \times c = b \times c\). +) Nếu \(a=b\) và \(a\;b\) cùng chia hết cho \(c\) (\(c\) khác \(0\)) thì \(a: c = b :c\). + Muốn nhân một số thập phân với \(100\) ta chỉ việc chuyển dấu phẩy của số đó sang bên phải hai chữ số. Cách giải: a) \(\overline {a,bc} \times \overline {xx} = 77,33\) \(\overline {a,bc} \times 100 \times \overline {xx} = 77,33 \times 100\) (cùng nhân với \(100\)) \(\overline {abc} \times \overline {xx} = 7733\) \(\overline {abc} \times x \times 11 = 703 \times 11\) \(\overline {abc} \times x = 703\) (cùng giảm 11 lần) \(703\) là số lẻ, suy ra \(\overline {abc} \) và \(x\) đều là số lẻ. Vậy \(x\) chỉ có thể \(1, 3, 5, 7, 9\). Nhưng 703 chỉ chia hết cho 1 và chính nó nên \(x = 1\). \(\overline {abc} \times 1 = 703\) \(\overline {abc} = 703:1 = 703\) Thử lại: \(7,03 \times 11 = 77,33.\) Vậy số thập phân \(\overline {a,bc} \) là \(7,03\) và \(x = 1.\) Đáp số : \(7,03\) và \(x = 1.\) Câu 7. Phương pháp: - Vẽ sơ đồ biểu diễn số ki-lô-mét đi được trong mỗi giờ. - Dựa vào sơ đồ để tìm số ki-lô-mét trung bình mỗi giờ đi được. - Tính độ dài quãng đường AB ta lấy số ki-lô-mét trung bình mỗi giờ đi được nhân với thời gian ô tô đi hết quãng đường AB. Cách giải: Nhìn vào sơ đồ ta thấy trung bình 1 giờ ô tô đi được số ki-lô-mét: \(48,75 - 4,15 + 5,45 = 50,05\;(km)\) Quãng đường AB dài là: \(50,05 \times 3 = 150,15\;(km)\) Đáp số: \(150,15km\). HocTot.Nam.Name.Vn
|