Bài 2 : Ôn tập : Tính chất cơ bản của phân sốGiải bài tập 1, 2, 3 trang 4 VBT toán 5 bài 2 : Ôn tập : Tính chất cơ bản của phân số với lời giải chi tiết và cách giải nhanh, ngắn nhất
Lựa chọn câu để xem lời giải nhanh hơn
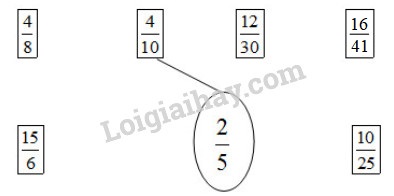
Bài 1 Video hướng dẫn giải Rút gọn các phân số 1830=.....3627=.....6480=.....4535=..... Phương pháp giải: Khi rút gọn phân số có thể làm như sau: - Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1. - Chia tử số và mẫu số cho số đó. Cứ làm như thế cho đến khi nhận được phân số tối giản. Lời giải chi tiết: 1830=18:630:6=35 ; 3627=36:927:9=43 ; 6480=64:880:8=810=8:210:2=45 ; 4535=45:535:5=97 Bài 2 Video hướng dẫn giải Quy đồng mẫu số hai phân số a) 45 và 79 ; ;MSC=.....;45=.....;79=..... b) 56 và 1718 c) 38 và 712 Lưu ý: MSC là viết tắt của “Mẫu số chung”. Phương pháp giải: Khi quy đồng mẫu số hai phân số có thể làm như sau: - Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai. - Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất. Lời giải chi tiết: a) 45 và 79 MSC: 45 ; 45=4×95×9=3645; 79=7×59×5=3545. b) 56 và 1718 MSC: 18 ; 56=5×36×3=1518 ; Giữ nguyên phân số 1718. c) 38 và 712 MSC: 24 ; 38=3×38×3=924; 712=7×212×2=1424 Bài 3 Video hướng dẫn giải a) Nối với phân số bằng 25 (theo mẫu) :
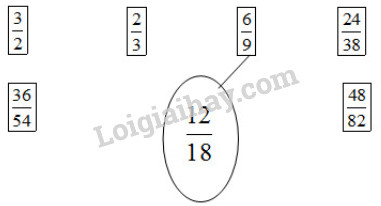
b) Nối với phân số bằng 1218 (theo mẫu) :
Phương pháp giải: Áp dụng tính chất cơ bản của phân số :
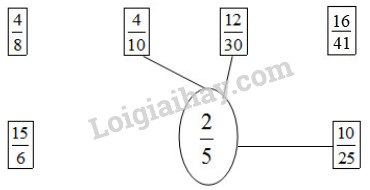
Lời giải chi tiết: a) Ta có : 25=2×25×2=410 ; 25=2×65×6=1230. 25=2×55×5=1025 Vậy ta có kết quả như sau :
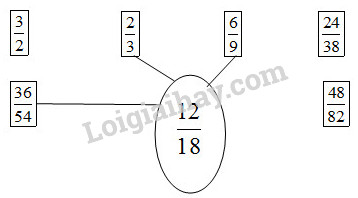
b) Ta có : 1218=12:618:6=23 ; 1218=12:218:2=69 1218=12×318×3=3654. Vậy ta có kết quả như sau :
HocTot.Nam.Name.Vn
>> Học trực tuyến các môn Toán, Tiếng Việt, Tiếng Anh lớp 5 trên Tuyensinh247.com. Cam kết giúp con lớp 5 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|