Bài 119 : Luyện tập chung

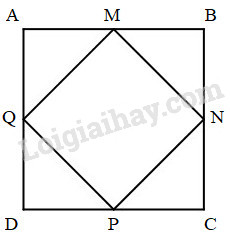
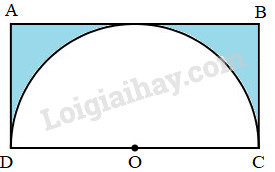
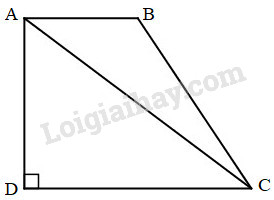
Bài 1

Cho hình vuông ABCD có cạnh 4cm. Trên các cạnh của hình vuông lấy lần lượt các trung điểm M, N, P, Q. Nối bốn điểm đó để được hình tứ giác MNPQ (xem hình vẽ). Tính tỉ số của diện tích hình tứ giác MNPQ và hình vuông ABCD.

Phương pháp giải:

- Diện tích hình vuông ABCD = cạnh × cạnh.

- Các tam giác AMQ, BMN, CPN, DPQ là các tam giác vuông có diện tích bằng nhau.

  Diện tích mỗi tam giác bằng tích độ dài hai cạnh góc vuông chia cho 2.

- Diện tích tích hình tứ giác MNPQ bằng diện tích hình vuông ABCD trừ đi tổng diện tích các tam giác AMQ, BMN, CPN, DPQ.

- Tìm tỉ số của diện tích hình tứ giác MNPQ và hình vuông ABCD ta lấy diện tích hình tứ giác MNPQ chia cho diện tích hình vuông ABCD.

Lời giải chi tiết:

Vì M, N, P, Q lần lượt là trung điểm của AB, BC, CD và AD nên ta có :

                  AM = MB = BN = NC = CP = PD = DQ = QA = 4 : 2 = 2cm

Diện tích hình vuông ABCD là :

                  4 × 4 = 16 (cm²)

Diện tích tam giác AMQ là :

                 2 × 2 : 2 = 2 (cm²)

Ta thấy các tam giác AMQ, BMN, CPN, DPQ có diện tích bằng nhau.

Diện tích tứ giác MNPQ là :

                  16 – (2 × 4) = 8 (cm²)

Tỉ số của diện tích hình tứ giác MNPQ và hình vuông ABCD là :

                 \(\displaystyle 8 : 16  = {1 \over 2}\)

                                         Đáp số :  \(\displaystyle{1 \over 2}\).

Bài 2

Cho hình bên gồm hình chữ nhật ABCD có AD = 2dm và một nửa hình tròn tâm O bán kính 2dm. Tính diện tích phần đã tô đậm của hình chữ nhật ABCD.

Phương pháp giải:

- Tìm chiều dài hình chữ nhật = OD ⨯ 2.

- Diện tích hình chữ nhật ABCD = chiều dài ⨯ chiều rộng.

- Diện tích nửa hình tròn tâm O = (bán kính ⨯ bán kính ⨯ 3, 14) : 2.

- Diện tích phần tô đậm = diện tích hình chữ nhật ABCD – diện tích nửa hình tròn tâm O.

Lời giải chi tiết:

Ta có bán kính OD = 2 dm, chiều dài hình chữ nhật ABCD là

2 x 2 = 4 (dm)

Diện tích hình chữ nhật ABCD là :

2 ⨯ 4 = 8 (dm²)

Diện tích nửa hình tròn tâm O là :

(2 ⨯ 2 ⨯ 3,14) : 2 = 6,28 (dm²)

Diện tích phần đã tô đậm là : 

8 – 6,28 = 1,72 (dm²)

                    Đáp số : 1,72dm².

Bài 3

Cho hình thang vuông ABCD (xem hình vẽ) có AB = 20cm, AD = 30cm, DC = 40cm.

Nối A với C được hai hình tam giác là ABC và ADC. Tính :

a) Diện tích mỗi hình tam giác đó. 

b) Tỉ số phần trăm của diện tích hình tam giác ABC và hình tam giác ADC.

Phương pháp giải:

- Diện tích hình thang ABCD = (đáy lớn + đáy bé) ⨯ chiều cao : 2 = (AB + DC) ⨯ AD : 2 .

- Diện tích tam giác ADC = AD ⨯ DC : 2.

- Diện tích tam giác ABC = diện tích hình thang ABCD – diện tích tam giác ADC.

- Để tìm tỉ số phần trăm của diện tích tam giác ABC và hình tam giác ADC ta tìm thương của diện tích tam giác ABC và hình tam giác ADC, sau đó nhân thương tìm được với 100 và thêm kí hiệu % vào bên phải.

Lời giải chi tiết:

a) Diện tích hình thang ABCD là :

 \(\displaystyle {{\left( {20 + 40} \right) \times 30} \over 2} = 900\,\left( {c{m^2}} \right)\)

Diện tích tam giác ADC là :

 \(\displaystyle {{40 \times 30} \over 2} = 600\,\left( {c{m^2}} \right)\)

Diện tích tam giác ABC là :

\(900 – 600 = 300 (cm^2)\)

b) Tỉ số phần trăm của diện tích tam giác ABC và hình tam giác ADC là :

 \(300 : 600 = 0,5 = 50\% \) 

Đáp số : a) Diện tích tam giác ABC : \(300cm^2\) ;

                  Diện tích tam giác ADC : \(600cm^2 \)

                   b) \(50\% \).                                 

HocTot.Nam.Name.Vn