Bài 141 : Ôn tập về phân số (tiếp theo)

Bài 1

Khoanh vào chữ đặt trước câu trả lời đúng:

Phân số chỉ phần đã tô màu của băng giấy là :

A. \( \displaystyle{4 \over 5}\)                                                  B. \( \displaystyle{5 \over 4}\)

C. \( \displaystyle{4 \over 9}\)                                                  D. \( \displaystyle{5 \over 9}\)

Phương pháp giải:

Quan sát hình vẽ, tìm số phần được tô màu và tổng số phần. Phân số chỉ số phần đã tô màu có tử số là số số phần được tô màu và mẫu số là tổng số phần. 

Lời giải chi tiết:

Băng giấy được chia làm 9 phần bằng nhau, trong đó có 4 phần được tô màu, từ đó tìm được phân số chỉ số phần đã tô màu là \( \dfrac {4}{9}\)

Vậy phân số chỉ số phần đã tô màu là \( \dfrac {4}{9}\).

Chọn C.

Bài 2

Khoanh vào chữ đặt trước câu trả lời đúng :

Có 20 viên bi, trong đó có 3 viên bi nâu, 4 viên bi xanh, 5 viên bi đỏ, 8 viên bi vàng. Như vậy, \( \displaystyle{1 \over 5}\) số viên bi có màu :

A. Nâu                                           B. Xanh

C. Đỏ                                             D. Vàng

Phương pháp giải:

Để tìm \(\dfrac{1}{5}\) số viên bi ta lấy tổng số viên bi nhân với \(\dfrac{1}{5}\). Từ đó tìm được màu tương ứng của bi. 

Lời giải chi tiết:

\(\dfrac{1}{5}\) số viên bi gồm số viên bi là:

                      \(20 \times \dfrac{1}{5} =4\) (viên bi)

Vậy \(\dfrac{1}{5}\) số viên bi có màu xanh.

Chọn B.

Bài 3

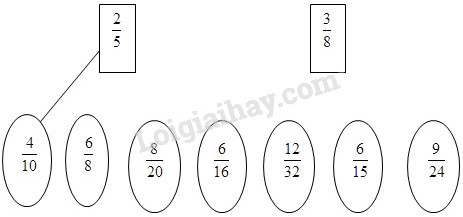
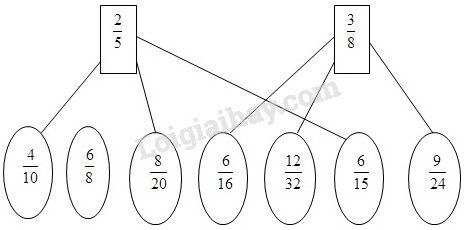
Nối \( \displaystyle{2 \over 5}\) hoặc \( \displaystyle{3 \over 8}\) với từng phân số bằng nó (theo mẫu) : 

Phương pháp giải:

Rút gọn các phân số thành phân số tối giản, từ đó tìm các phân số bằng nhau. 

Lời giải chi tiết:

\(\dfrac{6}{8}=\dfrac{6:2}{8:2}=\dfrac{3}{4}\) ;                                \(\dfrac{8}{20}=\dfrac{8:4}{20:4}=\dfrac{2}{5}\) ;

\(\dfrac{6}{16}=\dfrac{6:2}{16:2}=\dfrac{3}{8}\) ;                            \(\dfrac{12}{32}=\dfrac{12:4}{32:4}=\dfrac{3}{8}\) ;

\(\dfrac{6}{15}=\dfrac{6:3}{15:3}=\dfrac{2}{5}\)  ;                           \(\dfrac{9}{24}=\dfrac{9:3}{24:3}=\dfrac{3}{8}\).

Vậy ta có kết quả như sau :

Bài 4

So sánh các phân số :

a) \( \displaystyle{5 \over 7}\) và \(\displaystyle{4 \over 5}\).

b) \( \displaystyle{8 \over {11}}\) và \(\displaystyle{5 \over 9}\).

c) \( \displaystyle{8 \over 9}\) và \(\displaystyle{9 \over 8}\).

Phương pháp giải:

Sử dụng các phương pháp so sánh phân số như:

- Quy đồng mẫu số hai phân số rồi so sánh.

- So sánh với 1. 

Lời giải chi tiết:

a) \( \displaystyle{5 \over 7}\) và \( \displaystyle {4 \over 5}\)

Quy đồng mẫu số :

\( \displaystyle\eqalign{
& {5 \over 7} = {{5 \times 5} \over {7 \times 5}} = {{25} \over {35}}; \cr 
& {4 \over 5} = {{4 \times 7} \over {5 \times 7}} = {{28} \over {35}} \cr 
& Vì\,{{25} \over {35}} < {{28} \over {35}}\,nên\,{5 \over 7} < {4 \over 5} \cr} \)

b) \( \displaystyle{8 \over {11}}\) và \( \displaystyle {5 \over 9}\)

Quy đồng mẫu số :

\( \displaystyle\eqalign{
& {8 \over {11}} = {{8 \times 9} \over {11 \times 9}} = {{72} \over {99}} ;\cr 
& {5 \over 9} = {{5 \times 11} \over {9 \times 11}} = {{55} \over {99}} \cr 
& Vì\,{{72} \over {99}} > {{55} \over {99}}\,nên\,{8 \over {11}} > {5 \over 9} \cr} \)

c) \( \displaystyle{8 \over 9}\) và \( \displaystyle {9 \over 8}\)

Cách 1:

Quy đồng mẫu số :

\( \displaystyle\eqalign{
& {8 \over 9} = {{8 \times 8} \over {9 \times 8}} = {{64} \over {72}} \cr 
& {9 \over 8} = {{9 \times 9} \over {8 \times 9}} = {{81} \over {72}} \cr 
& Vì\,{{64} \over {72}} < {{81} \over {72}}\,nên\,{8 \over 9} < {9 \over 8} \cr} \)

Cách 2:

Vì \( \displaystyle \,{8 \over 9} < 1 \) và \( \displaystyle {9 \over 8} > 1 \) nên \(\displaystyle {8 \over 9} < {9 \over 8}. \)

Bài 5

Viết các phân số \( \displaystyle{9 \over {14}};{9 \over {15}};{3 \over 4}\) theo thứ tự từ bé đến lớn.

Phương pháp giải:

Quy đồng tử số rồi so sánh các phân số, sau đó sắp xếp các phân số theo thứ tự từ bé đến lớn. 

Lời giải chi tiết:

Chọn tử số chung là 9.

Ta có : \(\displaystyle {3 \over 4} = {{3 \times 3} \over {4 \times 3}} = {{9} \over {12}}\).

Vì \( \displaystyle {9 \over {15}} < {9 \over {14}} < {9 \over {12}}\) (do \(15 >14>12\)) nên  \( \displaystyle {9 \over {15}} < {9 \over {14}} < {3 \over 4} .\)

Vậy các phân số đã cho được sắp xếp theo thứ tự từ bé đến lớn là : \( \displaystyle {9 \over {15}} \;;\; {9 \over {14}} \;;\; {3 \over 4} .\)

HocTot.Nam.Name.Vn