Đề kiểm tra học kì 1 Toán 5 - Đề số 15Tải vềĐáp án và lời giải chi tiết Đề số 10 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán lớp 5
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
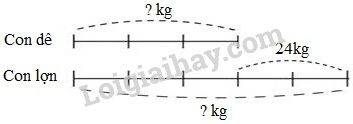
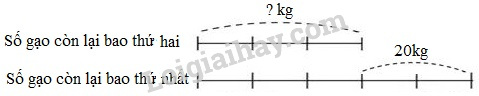
Đề bài Câu 1. Đúng ghi Đ, sai ghi S: Điền dấu \(\left( { > , = , < } \right)\)vào chỗ chấm: a) 20km 5m ......... 20050m 20km 5m > 20050m ☐ 20km 5m = 20050m ☐ 20km 5m < 20050m ☐ b) 3kg 15g ......... 3015g 3kg 15g > 3015g ☐ 3kg 15g = 3015g ☐ 3kg 15g < 3015g ☐ Câu 2. Đúng ghi Đ, sai ghi S: a) 3 tấn 25kg = \(3\dfrac{{25}}{{100}}\) tấn ☐ b) 3 tấn 25kg = \(3\dfrac{{25}}{{1000}}\) tấn ☐ c) 4km 8m = \(4\dfrac{8}{{10}}\) km ☐ d) 4km 8m = \(4\dfrac{8}{{1000}}\) km ☐ Câu 3. Khoanh vào chữ đặt trước câu trả lời đúng: Con lợn nặng hơn con dê 24kg. Biết \(\dfrac{1}{3}\) con dê nặng bằng \(\dfrac{1}{5}\) con lợn. Hỏi cả hai con nặng bao nhiêu ki-lô-gam? A.72kg B. 96kg C. 120kg Câu 4. Bao nhiêu thứ nhất có nhiều hơn bao thứ hai 40kg gạo. Sau khi mỗi bao bán đi 20kg gạo thì số gạo còn lại ở bao thứ hai bằng \(\dfrac{3}{5}\) số gạo ở bao thứ nhất. Hỏi lúc đầu mỗi bao có bao nhiêu ki-lô-gam gạo? Câu 5. Một bồn hoa hình tam giác. Tổng số đo cạnh thứ nhất và cạnh thứ hai là \(2\dfrac{4}{5}\)m. Tổng số đo cạnh thứ hai và cạnh thứ ba là \(\dfrac{{18}}{5}m\). Tổng số đo cạnh thứ ba và cạnh thứ nhất là \(3\dfrac{2}{{10}}m\). Tính số đo mỗi cạnh của bồn hoa. Lời giải Câu 1. Phương pháp: Đổi các số đo về cùng một đơn vị đo rồi so sánh kết quả với nhau. Lưu ý cách chuyển đổi: \(1km=1000m\) ; \(1kg =1000g\). Cách giải: a) \(20km \;5m = 20km+5m\)\(= 20000m +5m= 20005m\). Mà \(20005m<20050m\) Vậy: \(20km \;5m < 20050m \). Ta có kết quả là: S; S; Đ. b) 3kg 15g = 3015g Ta có kết quả là: S; Đ; S. Câu 2. Phương pháp: Dựa vào cách chuyển đổi các đơn vị đo: +) \(1\) tấn \(=1000kg\), hay \(1kg= \dfrac{1}{1000}\) tấn. +) \(1km=1000m\) hay \(1m= \dfrac{1}{1000}km\) Cách giải: \(3\) tấn \(25kg = 3\dfrac{{25}}{{1000}}\) tấn ; \(4km 8m = 4\dfrac{8}{{1000}}km\). Vậy ta có kết quả như sau: a) S ; b) Đ ; c) S ; d) Đ. Câu 3. Phương pháp: - Vì \(\dfrac{1}{3}\) con dê nặng bằng \(\dfrac{1}{5}\) con lợn nên nếu coi cân nặng của con dê gồm \(3\) phần bằng nhau thì cân nặng của con lợn gồm \(5\) phần như thế. - Tìm cân nặng của mỗi con theo dạng toán tìm hai số khi biết tổng và tỉ số của hai số đó. Cách giải: Vì \(\dfrac{1}{3}\) con dê nặng bằng \(\dfrac{1}{5}\) con lợn nên nếu coi cân nặng của con dê gồm \(3\) phần bằng nhau thì cân nặng của con lợn gồm \(5\) phần như thế. Ta có sơ đồ: Theo sơ đồ, hiệu số phần bằng nhau là: \(5-3 =2 \) (phần) Con dê cân nặng số ki-lô-gam là: \(24:2 \times 3 = 36\;(kg)\) Con lợn cân nặng số ki-lô-gam là: \(36+24 =60\;(kg)\) Cả hai con cân nặng số ki-lô-gam là: \( 36 + 60 = 96\;(kg)\) Đáp số: \(96kg.\) Chọn B. Câu 4. Phương pháp: - Nếu mỗi bao bán đi \(20kg\) gạo thì hiệu số gạo hai bao không thay đổi và bằng \(40kg\). - Ta tìm số gạo còn lại của mỗi bao theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số đó. - Tìm số gạo lúc đầu đầu của mỗi bao ta lấy số gạo còn lại cộng với số gạo đã bán đi. Cách giải: Nếu mỗi bao bán đi \(20kg\) gạo thì hiệu số gạo hai bao không thay đổi và bằng \(40kg\). Ta có sơ đồ: Theo sơ đồ, hiệu số phần bằng nhau là: \(5-3 =2 \) (phần) Sau khi bán đi \(20kg\), bao thứ hai còn lại số gạo là: \(40:2 \times 3 = 60\;(kg)\) Lúc đầu bao thứ hai có số ki-lô-gam gạo là: \(60 + 20 = 80 \;(kg)\) Lúc đầu bao thứ nhất có số ki-lô-gam gạo là: \(80+ 40 = 120 \;(kg)\) Đáp số: Bao thứ nhất: \(120 kg\); Bao thứ hai: \(80kg\). Câu 5. Phương pháp: - Đổi các hỗn số về dạng phân số: \(2\dfrac{4}{5}= \dfrac{14}{5}\) ; \(3\dfrac{2}{10} =\dfrac{32}{10}= \dfrac{16}{5}\). - Từ đề bài ta có \(2\) lần tổng số đo ba cạnh của bồn hoa hay chu vi bồn hoa là: \({\dfrac{14}{5} + \dfrac{{18}}{5} + \dfrac{16}{{5}}}\), từ đó ta tìm được tổng số đo ba cạnh của bồn hoa hay chu vi bồn hoa. - Tìm số đo cạnh thứ nhất ta lấy chu vi bồn hoa trừ đi tổng số đo cạnh thứ hai và cạnh thứ ba. - Tìm số đo cạnh thứ hai ta có thể lấy chu vi bồn hoa trừ đi tổng số đo cạnh thứ nhất và cạnh thứ ba. - Tìm số đo cạnh thứ ba ta có thể lấy tổng số đo cạnh thứ hai và cạnh thứ ba trừ đi số đo cạnh thứ hai. Cách giải: \(2\) lần tổng số đo ba cạnh của bồn hoa hay \(2\) lần chu vi bồn hoa là: \(\dfrac{14}{5} + \dfrac{{18}}{5} + \dfrac{16}{{5}} = \dfrac{{48}}{5}\;(m)\) Tổng số đo ba cạnh của bồn hoa hay chu vi bồn hoa là: \( \dfrac{{48}}{5}:2 = \dfrac{{24}}{5}\;(m)\) Số đo cạnh thứ nhất là: \(\dfrac{{24}}{5} - \dfrac{{18}}{5} = \dfrac{6}{5}\;(m)\) Số đo cạnh thứ hai là: \(\dfrac{{24}}{5} - \dfrac{16}{{5}} = \dfrac{8}{5}\;(m)\) Số đo cạnh thứ ba là: \(\dfrac{{18}}{5} - \dfrac{8}{5} = 2(m)\) Đáp số: Cạnh thứ nhất: \(\dfrac{6}{5}m;\) Cạnh thứ hai: \(\dfrac{8}{5}m;\) Cạnh thứ ba: \(2m.\) HocTot.Nam.Name.Vn
|