Trắc nghiệm Bài tập ôn tập chương 7 Toán 8Đề bài
Câu 1 :
Cho hình vẽ biết DE//BC. Khẳng định nào sau đây là đúng? 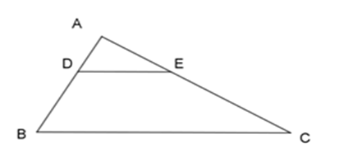
Câu 2 :
Chỉ ra câu sai?
Câu 3 :
Chỉ ra 1 tỉ số sai nếu ta áp dụng định lý Talet, biết ABCD là hình bình hành: 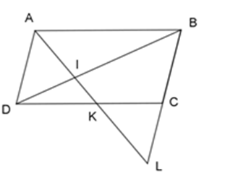
Câu 4 :
Cho 2 tam giác MNP và QRS đồng dạng với nhau theo tỉ số k. Tỷ số diện tích của 2 tam giác MNP và QRS là:
Câu 5 :
Cho \Delta MNP \backsim \Delta HGK có tỉ số chu vi: \dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7} khi đó:
Câu 6 :
Cho \Delta ABC và \Delta XYZ đồng dạng. Đỉnh A tương ứng với đỉnh X, đỉnh B tương ứng với đỉnh Y. Biết AB = 3,{\rm{ }}BC = 4 và XY = 5. Tính YZ ?
Câu 7 :
Cho \Delta ABC có AB = 4{\rm{ }}cm,{\rm{ }}BC = 6{\rm{ }}cm,{\rm{ }}AC = 5{\rm{ }}cm. \Delta MNP có MN = 3{\rm{ }}cm,{\rm{ }}NP = 2,5{\rm{ }}cm,{\rm{ }}PM = 2{\rm{ }}cm thì tỉ lệ \dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta ABC}}}} bằng bao nhiêu?
Câu 8 :
Cho biết \dfrac{{AB}}{{CD}} = \dfrac{5}{7} và đoạn thẳng AB ngắn hơn đoạn thẳng CD là 10{\rm{ }}cm. Tính độ dài các đoạn thẳngAB,{\rm{ }}CD ?
Câu 9 :
Cho \Delta ABC, đường phân giác góc B cắt AC tại D và cho biết AB = 10{\rm{ }}cm,{\rm{ }}BC = 15{\rm{ }}cm,{\rm{ }}AD = 6{\rm{ }}cm. Tính AC = ?
Câu 10 :
Tìm y trong hình vẽ dưới đây. 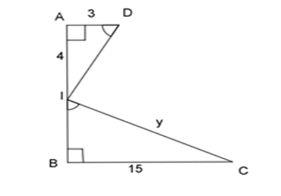
Câu 11 :
Cho biết ABCD là hình chữ nhật. Tìm x. 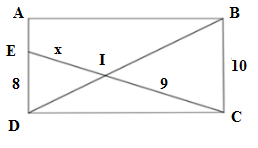
Câu 12 :
Cho đoạn AC vuông góc với CE. Nối A với trung điểm D của CE và E với trung điểm B của AC,{\rm{ }}AD và EB cắt nhau tại F. Cho BC = CD = 15{\rm{ }}cm. Tính diện tích tam giác DEF theo đơn vị c{m^2} ?
Câu 13 :
Cho tam giác ABC có {\rm{ }}BC = 8{\rm{ }}cm;{\rm{ }}BH và CK ( H \in AC;\, K \in AB) là hai đường trung tuyến kẻ từ B và C. Tính độ dài đoạn HK.
Câu 14 :
Một người đo chiều cao của cây nhờ 1 cọc chôn xuống đất, cọc cao 2,45 m và đặt xa cây 1,36 m. Sau khi người ấy lùi ra xa cách cọc 0,64 m thì người ấy nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu? Biết khoảng cách từ chân đến mắt người ấy là 1,65 m.
Câu 15 :
Tỉ số các cạnh bé nhất của 2 tam giác đồng dạng bằng \dfrac{2}{5}. Tính chu vi p, p' của 2 tam giác đó, biết p' - p = 18?
Câu 16 :
Cho \Delta A'B'C' \backsim \Delta ABC. Biết {S_{\Delta A'B'C'}} = \dfrac{{25}}{{49}}{S_{\Delta ABC}} và hiệu 2 chu vi của 2 tam giác là 16 m. Tính chu vi mỗi tam giác?
Câu 17 :
Cho \Delta A'B'C' đồng dạng với \Delta ABC có chu vi lần lượt là 50 cm và 60 cm. Diện tích của \Delta ABC lớn hơn diện tích của \Delta A'B'C' là 33 cm^2. Tính diện tích tam giác ABC.
Câu 18 :
Cho hình bình hành ABCD, điểm F nằm trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chọn câu đúng nhất.
Câu 19 :
Cho tam giác MNP vuông ở M và có đường cao MK .
Câu 20 :
Cho hình chữ nhật ABCD có E là trung điểm của AB. Tia DE cắt AC ở F, cắt CB ở G. Chọn câu đúng.
Câu 21 :
Cho \Delta ABC vuông tại A, đường cao AH. Gọi I và K lần lượt là hình chiếu của H lên AB và AC. Tam giác AIK đồng dạng với tam giác nào dưới đây?
Lời giải và đáp án
Câu 1 :
Cho hình vẽ biết DE//BC. Khẳng định nào sau đây là đúng? 
Đáp án : A Phương pháp giải :
- Áp dụng định lý Talet, hệ quả định lý Ta-lét để tìm ra tỉ lệ thức phù hợp, từ đó thực hiện yêu cầu của bài toán. Lời giải chi tiết :
Áp dụng hệ quả định lý Ta lét, ta có: \dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} = \dfrac{{DE}}{{BC}} \Rightarrow Đáp án A đúng. + Vì \dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} nên AD.AC = AB.AE \Rightarrow Đáp án B sai. + Ta có: \dfrac{{DE}}{{BC}}=\dfrac{{AD}}{{AB}} \ne \dfrac{{AD}}{{DB}} (hệ quả định lý Ta-lét) \Rightarrow Đáp án C sai. + Ta có: \dfrac{{AD}}{{AB}} = \dfrac{{DE}}{{BC}} \Rightarrow AD.BC = AB.DE \Rightarrow Đáp án D sai.
Câu 2 :
Chỉ ra câu sai?
Đáp án : C Phương pháp giải :
- Vận dụng kiến thức về tam giác đồng dạng. - Chú ý rằng: Hai tam giác bằng nhau cũng là hai tam giác đồng dạng với tỉ số đồng dạng là 1. Lời giải chi tiết :
Giả sử ta có: \Delta ABC = \Delta A'B'C' \Rightarrow \widehat A = \widehat {A'},\;\widehat B = \widehat {B'} (các cặp góc tương ứng bằng nhau) \Rightarrow \Delta ABC \backsim \Delta A'B'C'\;(g - g) \Rightarrow Đáp án A, B đúng. + Giả sử xét 2 tam giác \Delta ABC và \Delta A'B'C' có: \dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} Điều kiện trên chưa đủ để chứng minh \Delta ABC \backsim \Delta A'B'C'. \Rightarrow Đáp án C sai. + Vì hai tam giác bằng nhau thì có diện tích bằng nhau \Rightarrow Đáp án D đúng.
Câu 3 :
Chỉ ra 1 tỉ số sai nếu ta áp dụng định lý Talet, biết ABCD là hình bình hành: 
Đáp án : B Phương pháp giải :
- Áp dụng định lý Talet tìm ra tỉ lệ thức đúng, từ đó chọn ra tỉ lệ thức sai. Lời giải chi tiết :
Có CD//AB (vì ABCD là hình bình hành) Suy ra: CK//AB; KD//AB;CL//AD Vì CK//AB nên áp dụng định lý Talet ta có: \dfrac{{LC}}{{LB}} = \dfrac{{LK}}{{LA}} Vì KD//AB nên áp dụng định lý Talet ta có: Có BC//AD (vì ABCD là hình bình hành) Suy ra: CL//AD Vì CL//AD nên áp dụng định lý Talet ta có:\dfrac{{KA}}{{KL}} = \dfrac{{KD}}{{KC}} Vậy \dfrac{{IB}}{{IK}} = \dfrac{{IA}}{{ID}} sai.
Câu 4 :
Cho 2 tam giác MNP và QRS đồng dạng với nhau theo tỉ số k. Tỷ số diện tích của 2 tam giác MNP và QRS là:
Đáp án : C Phương pháp giải :
+ Tỉ số diện tích bằng bình phương tỉ số đồng dạng Lời giải chi tiết :
Giả sử \Delta MNP \backsim \Delta QRS theo tỉ số k thì tỉ số diện tích \dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta QRS}}}} = {k^2}
Câu 5 :
Cho \Delta MNP \backsim \Delta HGK có tỉ số chu vi: \dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7} khi đó:
Đáp án : A Phương pháp giải :
- Áp dụng lý thuyết về mối quan hệ giữa tỉ số diện tích hai tam giác đồng dạng và tỉ số đồng dạng của 2 tam giác, kết hợp với dữ kiện đề bài cho để thực hiện yêu cầu của bài toán. Lời giải chi tiết :
Gọi k là tỉ số đồng dạng của 2 tam giác MNP và HGK. Theo bài ta có: \Delta MNP \backsim \Delta HGK và \dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7} \Rightarrow \dfrac{{MN}}{{HG}} = \dfrac{{NP}}{{GK}} = \dfrac{{MP}}{{HK}} = \dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7} = k \Rightarrow \dfrac{{HG}}{{MN}} = \dfrac{7}{2} \Rightarrow \dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = {k^2} = {\left( {\dfrac{2}{7}} \right)^2} = \dfrac{4}{{49}}. Chú ý
- Học sinh cần chú ý trong kĩ năng đại số tránh mắc sai lầm trong tính toán. - Học sinh cần chú ý tránh nhầm lẫn giữa tỉ số đồng dạng và tỉ số diện tích hai tam giác đồng dạng.
Câu 6 :
Cho \Delta ABC và \Delta XYZ đồng dạng. Đỉnh A tương ứng với đỉnh X, đỉnh B tương ứng với đỉnh Y. Biết AB = 3,{\rm{ }}BC = 4 và XY = 5. Tính YZ ?
Đáp án : D Phương pháp giải :
- Từ cặp tam giác đồng dạng tìm ra tỉ lệ thức phù hợp, từ đó tìm ra độ dài của YZ. Lời giải chi tiết :
Theo bài ta có: \Delta ABC \backsim \Delta XYZ \Rightarrow \dfrac{{AB}}{{XY}} = \dfrac{{BC}}{{YZ}} \Leftrightarrow \dfrac{3}{5} = \dfrac{4}{{YZ}} \Rightarrow YZ = \dfrac{{5.4}}{3} = \dfrac{{20}}{3} = 6\dfrac{2}{3}
Câu 7 :
Cho \Delta ABC có AB = 4{\rm{ }}cm,{\rm{ }}BC = 6{\rm{ }}cm,{\rm{ }}AC = 5{\rm{ }}cm. \Delta MNP có MN = 3{\rm{ }}cm,{\rm{ }}NP = 2,5{\rm{ }}cm,{\rm{ }}PM = 2{\rm{ }}cm thì tỉ lệ \dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta ABC}}}} bằng bao nhiêu?
Đáp án : B Phương pháp giải :
- Chứng minh 2 tam giác đã cho đồng dạng, tìm ra tỉ số đồng dạng k, từ đó tìm ra tỉ lệ diện tích của 2 tam giác. Lời giải chi tiết :
Ta có: \dfrac{{MN}}{{BC}} = \dfrac{3}{6} = \dfrac{1}{2},\;\dfrac{{PN}}{{CA}} = \dfrac{{2,5}}{5} = \dfrac{1}{2},\;\dfrac{{PM}}{{AB}} = \dfrac{2}{4} = \dfrac{1}{2} \Rightarrow \dfrac{{MN}}{{BC}} = \dfrac{{PN}}{{CA}} = \dfrac{{PM}}{{AB}} = \dfrac{1}{2} Vậy \Delta PMN \backsim \Delta ABC\;(c - c - c) Suy ra tỉ số đồng dạng k của hai tam giác là k = \dfrac{{MN}}{{BC}} = \dfrac{1}{2}. \Rightarrow \dfrac{{{S_{\Delta PMN}}}}{{{S_{\Delta ABC}}}} = {k^2} = {\left( {\dfrac{1}{2}} \right)^2} = \dfrac{1}{4}
Câu 8 :
Cho biết \dfrac{{AB}}{{CD}} = \dfrac{5}{7} và đoạn thẳng AB ngắn hơn đoạn thẳng CD là 10{\rm{ }}cm. Tính độ dài các đoạn thẳngAB,{\rm{ }}CD ?
Đáp án : C Phương pháp giải :
- Từ tỉ số đoạn thẳng ta biểu diễn AB theo CD - Thay vào điều kiện đề bài cho để tính CD, từ đó ta tính được AB Lời giải chi tiết :
Theo bài ra, ta có: \dfrac{{AB}}{{CD}} = \dfrac{5}{7} \Rightarrow AB = \dfrac{5}{7}CD Mà đoạn thẳng AB ngắn hơn đoạn thẳng CD là 10{\rm{ }}cm, suy ra: CD - AB = 10. \begin{array}{l} \Rightarrow CD - \dfrac{5}{7}CD = 10 \Leftrightarrow \dfrac{2}{7}CD = 10 \Leftrightarrow CD = \dfrac{{10.7}}{2} = 35\;cm\\ \Rightarrow AB = \dfrac{5}{7}CD = \dfrac{5}{7}.35 = 25\;cm\end{array} Chú ý
- Học sinh cần chú ý trong kĩ năng đại số tránh mắc sai lầm trong tính toán
Câu 9 :
Cho \Delta ABC, đường phân giác góc B cắt AC tại D và cho biết AB = 10{\rm{ }}cm,{\rm{ }}BC = 15{\rm{ }}cm,{\rm{ }}AD = 6{\rm{ }}cm. Tính AC = ?
Đáp án : D Phương pháp giải :
- Áp dụng tính chất đường phân giác để tính DC. - Từ đó tính AC=AD+DC Lời giải chi tiết :
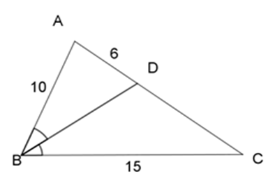 Áp dụng tính chất đường phân giác trong tam giác ABC, ta có: \dfrac{{BA}}{{AD}} = \dfrac{{BC}}{{CD}} \Rightarrow \dfrac{{10}}{6} = \dfrac{{15}}{{CD}} \Leftrightarrow CD = \dfrac{{6.15}}{{10}} = 9\;cm \Rightarrow AC = AD + DC = 6 + 9 = 15\;cm Chú ý
- Học sinh cần chú ý tránh mắc sai lầm trong tính toán. - Một số em sau khi tính DC thì chọn luôn mà không tính AC nên chọn sai đáp án.
Câu 10 :
Tìm y trong hình vẽ dưới đây. 
Đáp án : C Phương pháp giải :
- Tính ID theo Pytago - Áp dụng các phương pháp chứng minh tam giác đồng dạng để tìm ra cặp tam giác đồng dạng phù hợp. - Suy ra tỉ lệ thức phù hợp, biến đổi tỉ lệ thức để tính giá trị của x. Lời giải chi tiết :
Áp dụng định lý Pitago trong tam giác vuông IAD ta có: \begin{array}{l}\;\;\;\;A{I^2} + A{D^2} = I{D^2}\;\;\\ \Leftrightarrow {4^2} + {3^2} = I{D^2}\\ \Leftrightarrow I{D^2} = 25\\ \Rightarrow ID = 5\end{array} Xét 2 tam giác vuông IAD và CBI có: \widehat {IDA} = \widehat {CIB}\;(gt) \Rightarrow \Delta IAD \backsim \Delta CBI\;(g - g) \Rightarrow \dfrac{{IA}}{{CB}} = \dfrac{{ID}}{{CI}} \Leftrightarrow \dfrac{4}{{15}} = \dfrac{5}{y} \Leftrightarrow y = \dfrac{{15.5}}{4} = 18,75 Vậy y = 18,75. Chú ý
- Học sinh cần viết tỉ lệ đồng dạng theo đúng thứ tự đỉnh, cạnh tương ứng của 2 tam giác. - Học sinh cần chú ý trong kĩ năng đại số tránh mắc sai lầm trong tính toán.
Câu 11 :
Cho biết ABCD là hình chữ nhật. Tìm x. 
Đáp án : A Phương pháp giải :
- Áp dụng các phương pháp chứng minh tam giác đồng dạng để tìm ra cặp tam giác đồng dạng phù hợp. - Suy ra tỉ lệ thức phù hợp, biến đổi tỉ lệ thức để tính giá trị của x. Lời giải chi tiết :
Xét tam giác BCI và tam giác DEI có: \widehat {CBI} = \widehat {EDI} (cặp góc so le trong) \widehat {EID} = \widehat {CIB} (2 góc đối đỉnh) \Rightarrow \Delta BCI \backsim \Delta DEI\;(g - g) \Rightarrow \dfrac{{CI}}{{EI}} = \dfrac{{BC}}{{DE}} \Leftrightarrow \dfrac{9}{x} = \dfrac{{10}}{8} \Leftrightarrow x = \dfrac{{9.8}}{{10}} = 7,2 Vậy x = 7,2.
Câu 12 :
Cho đoạn AC vuông góc với CE. Nối A với trung điểm D của CE và E với trung điểm B của AC,{\rm{ }}AD và EB cắt nhau tại F. Cho BC = CD = 15{\rm{ }}cm. Tính diện tích tam giác DEF theo đơn vị c{m^2} ?
Đáp án : C Phương pháp giải :
- Kẻ FH vuông góc với CE (H thuộc CE ). - Chỉ ra hai tam giác đồng dạng - Áp dụng tính chất đường trung tuyến của tam giác để tìm ra tỉ số của cặp cạnh, suy ra độ dài cạnh FH cần tìm. - Tính diện tích tam giác DEF. Lời giải chi tiết :
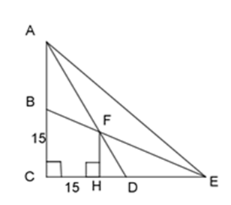 Xét \Delta EAC có AD,{\rm{ }}EB là 2 đường trung tuyến. Suy ra F là giao của 2 đường trung tuyến AD,{\rm{ }}EB nên F là trọng tâm của tam giác ABC. \Rightarrow \dfrac{{EF}}{{EB}} = \dfrac{{AF}}{{AD}} = \dfrac{2}{3}. Kẻ FH vuông góc với CE (H thuộc CE ). Xét 2 tam giác vuông EFH và EBC ta có: \widehat {BEC} chung \Rightarrow \Delta EFH \backsim \Delta EBC (g-g) \Rightarrow \dfrac{{EF}}{{EB}} = \dfrac{{FH}}{{BC}} = \dfrac{2}{3} \Rightarrow \dfrac{{FH}}{{15}} = \dfrac{2}{3} \Rightarrow FH = \dfrac{{2.15}}{3} = 10\;cm Vì D là trung điểm của CE nên CD = DE = 15 cm. Vậy diện tích của tam giác DEF là: {S_{\Delta DEF}} = \dfrac{1}{2}.FH.DE = \dfrac{1}{2}.10.15 = 75\;c{m^2} Chú ý
- Học sinh cần viết tỉ lệ đồng dạng theo đúng thứ tự đỉnh, cạnh tương ứng của 2 tam giác. - Học sinh cần kẻ thêm hình để giải bài toán, đối với những bài toán không thể giải theo phương pháp thông thường. - Học sinh cần chú ý trong kĩ năng đại số tránh mắc sai lầm trong tính toán.
Câu 13 :
Cho tam giác ABC có {\rm{ }}BC = 8{\rm{ }}cm;{\rm{ }}BH và CK ( H \in AC;\, K \in AB) là hai đường trung tuyến kẻ từ B và C. Tính độ dài đoạn HK.
Đáp án : B Phương pháp giải :
Cách 1: Sử dụng tính chất đường trung bình của tam giác Cách 2: Áp dụng cách chứng minh tam giác đồng dạng rồi suy ra tỉ lệ cạnh Lời giải chi tiết :
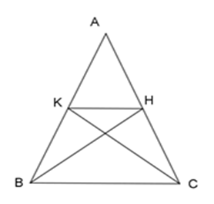 Ta lại có BH và CK là hai đường trung tuyến kẻ từ B và C của tam giác ABC, suy ra H và K lần lượt là trung điểm của AC và AB. nên HK là đường trung bình của tam giác ABC nên HK= \dfrac{1}{2} BC=\dfrac{8}{2} = 4\;cm
Câu 14 :
Một người đo chiều cao của cây nhờ 1 cọc chôn xuống đất, cọc cao 2,45 m và đặt xa cây 1,36 m. Sau khi người ấy lùi ra xa cách cọc 0,64 m thì người ấy nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu? Biết khoảng cách từ chân đến mắt người ấy là 1,65 m.
Đáp án : D Phương pháp giải :
- Tìm ra các cặp tam giác đồng dạng phù hợp. - Áp dụng tính chất của tam giác đồng dạng để tìm ra yêu cầu của đề bài. Lời giải chi tiết :
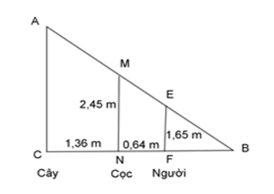 Ta mô tả vị trí cây, cọc và người như hình vẽ bên. Xét \Delta BFE và \Delta BNM ta có: \widehat B\;chung \widehat {BEF} = \widehat {BMN} (vì EF//MN, cặp góc đồng vị bằng nhau) \Rightarrow \Delta BFE \backsim \Delta BNM\;(g - g) \begin{array}{l} \Rightarrow \dfrac{{BF}}{{BN}} = \dfrac{{FE}}{{NM}} \Leftrightarrow \dfrac{{BF}}{{BF + FN}} = \dfrac{{FE}}{{NM}} \Leftrightarrow \dfrac{{BF}}{{BF + 0,64}} = \dfrac{{1,65}}{{2,45}}\\ \Leftrightarrow 1,65\left( {BF + 0,64} \right) = 2,45.BF\\ \Leftrightarrow BF = 1,32\;\;m.\end{array} Xét \Delta BFE và \Delta BCA có: \widehat B\;chung \widehat {BEF} = \widehat {BAC} (vì EF\parallel AC, cặp góc đồng vị bằng nhau) \Rightarrow \Delta BFE \backsim \Delta BCA\;(g - g) \begin{array}{l} \Rightarrow \dfrac{{BF}}{{BC}} = \dfrac{{FE}}{{CA}} \Leftrightarrow \dfrac{{BF}}{{BF + FN + NC}} = \dfrac{{FE}}{{CA}} \Leftrightarrow \dfrac{{1,32}}{{1,32 + 0,64 + 1,36}} = \dfrac{{1,65}}{{CA}}\\ \Rightarrow CA = 4,15\;m\end{array} Vậy cây cao đúng bằng độ dài của đoạn CA hay cây cao 4,15 m. Chú ý
- Học sinh cần viết tỉ lệ đồng dạng theo đúng thứ tự đỉnh, cạnh tương ứng của 2 tam giác. - Học sinh cần chú ý trong kĩ năng đại số tránh mắc sai lầm trong tính toán.
Câu 15 :
Tỉ số các cạnh bé nhất của 2 tam giác đồng dạng bằng \dfrac{2}{5}. Tính chu vi p, p' của 2 tam giác đó, biết p' - p = 18?
Đáp án : A Phương pháp giải :
- Từ dữ kiện đề bài cho, suy ra tỉ số đồng dạng phù hợp. - Tỉ số đồng dạng bằng tỉ số chu vi của 2 tam giác, kết hợp với dữ kiện đề bài, tìm chu vi của 2 tam giác. Lời giải chi tiết :
Giả sử 2 tam giác đồng dạng là ABC và DEF, 2 cạnh bé nhất của 2 tam giác lần lượt là AB và DE. Khi đó ta có: \dfrac{{AB}}{{DE}} = \dfrac{2}{5} Vì \Delta ABC \backsim \Delta DEF nên: \begin{array}{l}\dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{EF}} = \dfrac{{CA}}{{FD}} = \dfrac{{AB + BC + CA}}{{DE + EF + FD}} = \dfrac{2}{5}\\ \Rightarrow \dfrac{p}{{p'}} = \dfrac{2}{5} \Leftrightarrow p = \dfrac{2}{5}p'.\end{array} Ta lại có: p' - p = 18 \begin{array}{l} \Rightarrow p' - \dfrac{2}{5}p' = 18 \Leftrightarrow p' = 30\\ \Rightarrow p = \dfrac{2}{5}p' = 12\end{array} Chú ý
- Học sinh cần chú ý trong kĩ năng đại số tránh mắc sai lầm trong tính toán.
Câu 16 :
Cho \Delta A'B'C' \backsim \Delta ABC. Biết {S_{\Delta A'B'C'}} = \dfrac{{25}}{{49}}{S_{\Delta ABC}} và hiệu 2 chu vi của 2 tam giác là 16 m. Tính chu vi mỗi tam giác?
Đáp án : D Phương pháp giải :
- Áp dụng tỉ số diện tích của 2 tam giác để tìm ra tỉ số đồng dạng của hai tam giác, từ đó tính toán theo yêu cầu của bài toán. Lời giải chi tiết :
Theo bài ta có: {S_{\Delta A'B'C'}} = \dfrac{{25}}{{49}}{S_{\Delta ABC}} và . \Rightarrow \dfrac{{{S_{\Delta A'B'C'}}}}{{{S_{\Delta ABC}}}} = \dfrac{{25}}{{49}} Gọi k là tỉ số đồng dạng của 2 tam giác \Delta A'B'C' và \Delta ABC. Khi đó ta có: \dfrac{{{S_{\Delta A'B'C'}}}}{{{S_{\Delta ABC}}}} = {k^2} = \dfrac{{25}}{{49}} = {\left( {\dfrac{5}{7}} \right)^2} \Rightarrow k = \dfrac{5}{7} Vì \Delta A'B'C' \backsim \Delta ABC nên \dfrac{{{C_{\Delta A'B'C'}}}}{{{C_{\Delta ABC}}}} = k = \dfrac{5}{7}. \Rightarrow {C_{\Delta A'B'C'}} = \dfrac{5}{7}{C_{\Delta ABC}}. Ta lại có hiệu 2 chu vi của 2 tam giác là 16 m , suy ra: {C_{\Delta ABC}} - {C_{\Delta A'B'C'}} = 16 \Rightarrow {C_{\Delta ABC}} - \dfrac{5}{7}{C_{\Delta ABC}} = 16 \Leftrightarrow \dfrac{2}{7}{C_{\Delta ABC}} = 16 \Leftrightarrow {C_{\Delta ABC}} = \dfrac{{16.7}}{2} = 56\;m \Rightarrow {C_{\Delta A'B'C'}} = \dfrac{5}{7}{C_{\Delta ABC}} = \dfrac{5}{7}.56 = 40\;m Vậy{C_{\Delta A'B'C'}} = 40\;m,\;{C_{\Delta ABC}} = 56\;m. Chú ý
- Học sinh cần chú ý trong kĩ năng đại số tránh mắc sai lầm trong tính toán. - Học sinh cần chú ý tránh nhầm lẫn giữa tỉ số đồng dạng và tỉ số diện tích hai tam giác đồng dạng.
Câu 17 :
Cho \Delta A'B'C' đồng dạng với \Delta ABC có chu vi lần lượt là 50 cm và 60 cm. Diện tích của \Delta ABC lớn hơn diện tích của \Delta A'B'C' là 33 cm^2. Tính diện tích tam giác ABC.
Đáp án : D Phương pháp giải :
+ Sử dụng tỉ số đồng dạng bằng tỉ số chu vi, tỉ số diện tích bằng bình phương tỉ số đồng dạng Lời giải chi tiết :
Gọi k là tỉ số đồng dạng của 2 tam giác đã cho. Theo đề bài ta có: k = \dfrac{{{p_{\Delta A'B'C'}}}}{{{p_{\Delta ABC}}}} = \dfrac{{50}}{{60}} = \dfrac{5}{6}. \Rightarrow \dfrac{{{S_{\Delta A'B'C'}}}}{{{S_{\Delta ABC}}}} = {k^2} = \dfrac{{25}}{{36}} \Rightarrow {S_{\Delta A'B'C'}} = \dfrac{{25}}{{36}}{S_{\Delta ABC}} Ta lại có: {S_{\Delta ABC}} - {S_{\Delta A'B'C'}} = 33 \begin{array}{l} \Leftrightarrow {S_{ABC}} - \dfrac{{25}}{{36}}{S_{ABC}} = 33\\ \Leftrightarrow {S_{\Delta ABC}} = 108\;c{m^2}.\end{array} Chú ý
- Học sinh cần chú ý trong kĩ năng đại số tránh mắc sai lầm trong tính toán.
Câu 18 :
Cho hình bình hành ABCD, điểm F nằm trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chọn câu đúng nhất.
Đáp án : C Phương pháp giải :
- Áp dụng cách chứng minh tam giác đồng dạng để chứng minh các cặp tam giác đồng dạng. - Từ đó tìm ra tỉ lệ thức phù hợp để suy ra hệ thức đúng về cạnh. Lời giải chi tiết :
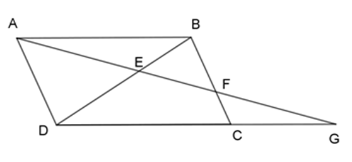 +) Vì ABCD là hình bình hành nên AD//BC \Rightarrow AD//BF (tính chất hbh). Xét \Delta BEF và \Delta DEA có: \widehat {BEF} = \widehat {DEA} (2 góc đối đỉnh) \widehat {FBE} = \widehat {ADE} (cặp góc so le trong bằng nhau) \Rightarrow \Delta BEF \backsim \Delta DEA\;(g - g) nên A sai. +) Vì ABCD là hình bình hành nên AB//DC \Rightarrow AB//DG Xét \Delta DGE và \Delta BAE ta có: \widehat {DEG} = \widehat {BEA} (2 góc đối đỉnh) \widehat {ABE} = \widehat {GDE} (cặp góc so le trong bằng nhau) \Rightarrow \Delta DGE \backsim \Delta BAE\;(g - g) nên B sai. +) Vì \Delta BEF \backsim \Delta DEA nên \dfrac{{EF}}{{EA}} = \dfrac{{BE}}{{DE}} (1) Vì \Delta DGE \backsim \Delta BAE nên \dfrac{{AE}}{{GE}} = \dfrac{{BE}}{{DE}} (2) Từ (1) và (2) ta có: \dfrac{{EF}}{{EA}} = \dfrac{{AE}}{{GE}} \Leftrightarrow A{E^2} = GE.EF nên C đúng. Chú ý
- Học sinh cần viết tỉ lệ đồng dạng theo đúng thứ tự đỉnh, cạnh tương ứng của 2 tam giác.
Câu 19 :
Cho tam giác MNP vuông ở M và có đường cao MK .
Đáp án : D Phương pháp giải :
- Áp dụng phương pháp chứng minh tam giác đồng dạng và biến đổi tỉ lệ thức để thực hiện yêu cầu của bài toán. Lời giải chi tiết :
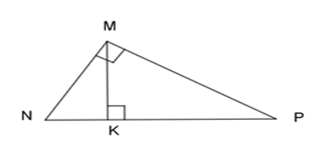 +) Xét 2 tam giác vuông \Delta KNM và \Delta MNP có: \widehat N chung nên \Delta KNM \backsim \Delta MNP (g.g) (1) Xét 2 tam giác vuông \Delta KMP và \Delta MNP có: \widehat P chung nên \Delta KMP \backsim \Delta MNP (g.g) (2) Từ (1) và (2) suy ra: \Delta KNM \backsim \Delta KMP (theo t/c bắc cầu). Vậy \Delta KNM \backsim \Delta MNP \backsim \Delta KMP nên A đúng. +) Theo chứng minh trên: \Delta KNM \backsim \Delta KMP. \Rightarrow \dfrac{{MK}}{{PK}} = \dfrac{{NK}}{{MK}} \Leftrightarrow M{K^2} = NK.PK nên B đúng. Vậy cả A, B đều đúng. Chú ý
- Học sinh cần viết tỉ lệ đồng dạng theo đúng thứ tự đỉnh, cạnh tương ứng của 2 tam giác.
Câu 20 :
Cho hình chữ nhật ABCD có E là trung điểm của AB. Tia DE cắt AC ở F, cắt CB ở G. Chọn câu đúng.
Đáp án : A Phương pháp giải :
+ Áp dụng phương pháp chứng minh tam giác bằng nhau + Định lý Talet và biến đổi tỉ lệ thức để tìm hệ thức đúng Lời giải chi tiết :
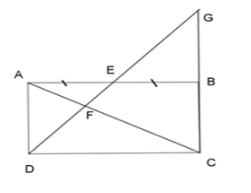 Ta có AB//CD(vì ABCD là hình chữ nhật) Áp dụng định lý Talet ta có: \dfrac{{EF}}{{FD}} = \dfrac{{AE}}{{DC}} Vì E là trung điểm của AB nên AE = EB = \dfrac{1}{2}AB = \dfrac{1}{2}CD \begin{array}{l} \Rightarrow \dfrac{{EF}}{{FD}} = \dfrac{{AE}}{{DC}} = \dfrac{1}{2}\;\;\left( 1 \right)\\ \Rightarrow FD = 2EF\;\end{array} Xét 2 tam giác vuông \Delta AED và \Delta BEG ta có: \begin{array}{l}\widehat {DAE} = \widehat {GBE} = {90^0}\\AE = EB\;\left( {gt} \right)\end{array} \widehat {AED} = \widehat {BEG} (2 góc đối đỉnh bằng nhau) \Rightarrow \Delta AED = \Delta BEG\;(g - c - g) \Rightarrow ED = EG (các cạnh tương ứng) Ta thấy: \dfrac{{FD}}{{FG}} = \dfrac{{2EF}}{{FE + EG}} = \dfrac{{2EF}}{{EF + ED}} = \dfrac{{2EF}}{{EF + EF + FD}} = \dfrac{{2EF}}{{EF + EF + 2EF}} = \dfrac{{2EF}}{{4EF}} = \dfrac{1}{2}(2) Từ (1) và (2) ta có: \dfrac{{EF}}{{FD}} = \dfrac{{FD}}{{FG}} \Leftrightarrow F{D^2} = EF.FG Chú ý
- Học sinh cần cặp tam giác bằng nhau theo đúng thứ tự đỉnh, cạnh tương ứng của 2 tam giác. - Học sinh cần chú ý trong kĩ năng biến đổi tỉ lệ thức tránh mắc sai lầm.
Câu 21 :
Cho \Delta ABC vuông tại A, đường cao AH. Gọi I và K lần lượt là hình chiếu của H lên AB và AC. Tam giác AIK đồng dạng với tam giác nào dưới đây?
Đáp án : A Phương pháp giải :
+ Chứng minh tứ giác AIHK là hình chữ nhật + Áp dụng các tính chất, định lý đã học và cách chứng minh đồng dạng của tam giác vuông để chứng minh yêu cầu của đề bài. Lời giải chi tiết :
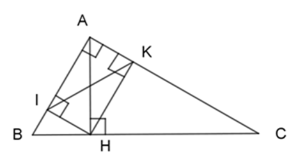 +) Có I, K lần lượt là hình chiếu của H lên AB và AC. \Rightarrow \widehat {HIA} = \widehat {HKA} = {90^0} Xét tứ giác AIHK có: \widehat {IAK} = \widehat {HIA} = \widehat {HKA} = {90^0} \Rightarrow Tứ giác AIHK là hình chữ nhật. (dhnb) +) Xét \Delta AIK và \Delta IAH ta có: AI\;chung AK = IH(theo tính chất của hình chữ nhật) AH = IK\; (theo tính chất của hình chữ nhật) \Rightarrow \Delta AIK = \Delta IAH\;(c - c - c) (1) Xét 2 tam giác vuông \Delta IAH và \Delta HAB có: \widehat A chung \Rightarrow \Delta IAH \backsim \Delta HAB\;(g - g) (2) Xét 2 tam giác vuông \Delta HAB và \Delta ACB có: \widehat B chung \Rightarrow \Delta HAB \backsim \Delta ACB\;\;\left( {g - g} \right) (3) Từ (1), (2) và (3) ta có: \Delta AIK \backsim \Delta ACB Chú ý
- Học sinh cần viết tỉ lệ đồng dạng theo đúng thứ tự đỉnh, cạnh tương ứng của 2 tam giác.
|












