Bài tập trắc nghiệm Toán 8

Trắc nghiệm Bài tập ôn tập chương 6 Toán 8

Làm đề thi

Đề bài

Câu 1 :

Đa giác đều là đa giác

A

Có tất cả các cạnh bằng nhau
B

Có tất cả các góc bằng nhau
C

Có tất cả các cạnh bằng nhau và các góc bằng nhau
D

Cả ba câu trên đều đúng

Câu 2 :

Hãy chọn câu đúng:

A

Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông
B

Diện tích hình chữ nhật bằng nửa tích hai kích thước của nó
C

Diện tích hình vuông có cạnh $a$ là $2a$
D

Tất cả các đáp án trên đều đúng

Câu 3 :

Một đa giác lồi $10$ cạnh thì có số đường chéo là:

A

$35$
B

$30$
C

$70$
D

$27$

Câu 4 :

Số đo mỗi góc của hình $9$ cạnh đều là:

A

$120^\circ$
B

$60^\circ$
C

$140^\circ$
D

$135^\circ$

Câu 5 :

Một tam giác có độ dài ba cạnh là $12cm,{\rm{ 5}}cm,{\rm{ 13}}cm.$ Diện tích tam giác đó là

A

$60c{m^2}$
B

$30c{m^2}$
C

$45c{m^2}$
D

$32,5c{m^2}$

Câu 6 :

Tổng số đo các góc của hình đa giác $n$ cạnh là $900^\circ$ thì

A

$n = 7$
B

$n = 8$
C

$n = 9$
D

$n = 6$

Câu 7 :

Hình chữ nhật có chiều dài tăng 4 lần, chiều rộng giảm 2 lần, khi đó diện tích hình chữ nhật

A

không thay đổi
B

tăng $4$ lần
C

giảm $2$ lần
D

tăng $2$ lần

Câu 8 :

Hình chữ nhật có diện tích là $240c{m^2}$ , chiều rộng là 8cm. Chu vi hình chữ nhật đó là:

A

$38cm$
B

$76cm$
C

$19cm$
D

$152cm$

Câu 9 :

Cho tam giác $ABC$ với ba đường cao $AA';\,BB';\,CC'$ . Gọi $H$ là trực tâm của tam giác đó. Chọn câu đúng.

A

$\dfrac{{HA'}}{{AA'}} + \dfrac{{HB'}}{{BB'}} + \dfrac{{HC'}}{{CC'}} = 1$
B

$\dfrac{{HA'}}{{AA'}} + \dfrac{{HB'}}{{BB'}} + \dfrac{{HC'}}{{CC'}} = 2$
C

$\dfrac{{HA'}}{{AA'}} + \dfrac{{HB'}}{{BB'}} + \dfrac{{HC'}}{{CC'}} = 3$
D

$\dfrac{{HA'}}{{AA'}} + \dfrac{{HB'}}{{BB'}} + \dfrac{{HC'}}{{CC'}} = 4$

Câu 10 :

Cho hình thang $ABCD{\rm{ }},{\rm{ }}AB$ song song với $CD,$ đường cao $AH.$ Biết $AB = 7cm;\,CD = 10cm$ , diện tích của $ABCD$ là $25,5c{m^2}$ thì độ dài $AH$ là:

A

2,5cm
B

3cm
C

3,5cm
D

5cm

Câu 11 :

Cho hình bình hành $ABCD,$ đường cao ứng với cạnh $DC$ là $AH = 6cm$ ; cạnh $DC = 12cm$ . Diện tích của hình bình hành $ABCD$ là:

A

$72c{m^2}$
B

$82c{m^2}$
C

$92c{m^2}$
D

$102c{m^2}$

Câu 12 :

Tính diện tích của tam giác đều $ABC$ biết chu vi tam giác $ABC$ bằng $18cm.$

A

$9\left( {c{m^2}} \right)$
B

$18\sqrt 3 \left( {c{m^2}} \right)$
C

$9\sqrt 3 \left( {c{m^2}} \right)$
D

$27\sqrt 3 \left( {c{m^2}} \right)$

Câu 13 :

Cho hình thoi $ABCD$ có hai đường chéo $AC$ và $BD$ cắt nhau tại $O.$ Biết $OA = 12cm$ , diện tích hình thoi $ABCD$ là $168c{m^2}$ . Cạnh của hình thoi là:

A

$\sqrt {190} (cm)$
B

$\sqrt {180} (cm)$
C

$\sqrt {193} (cm)$
D

$\sqrt {195} (cm)$

Câu 14 :

Cho tam giác $ABC$ trung tuyến $AM,$ chiều cao $AH$ . Chọn câu đúng

A

${S_{ABM}} = {S_{ACM}} = {S_{ABC}}$
B

${S_{ABM}} = {S_{ACM}} = \dfrac{1}{2}{S_{ABC}}$
C

${S_{ABM}} = {S_{ACB}} = \dfrac{1}{2}{S_{AMC}}$
D

${S_{ABM}} = \dfrac{1}{2}{S_{ACM}} = \dfrac{1}{2}{S_{ABC}}$

Câu 15 :

Cho hình chữ nhật ABCD có $AD = 8cm,\;AB = 9cm$ . Các điểm $M,{\rm{ }}N$ trên đường chéo $BD$ sao cho $BM = MN = ND.$ Tính diện tích tam giác $CMN.$

A

$12c{m^2}$
B

$24c{m^2}$
C

$36c{m^2}$
D

$6c{m^2}$

Câu 16 :

Cho hình chữ nhật $ABCD$ . Trên cạnh $AB$ lấy M . Tìm vị trí của M để ${S_{MBC}} = \dfrac{1}{4}{S_{ABCD}}$

A

$M$ là điểm thuộc đoạn $AB$ sao cho $AM = \dfrac{1}{2}MB$
B

$M$ là điểm thuộc đoạn $AB$ sao cho $AM = \dfrac{3}{4}AB$
C

$M$ là trung điểm đoạn $AB.$
D

$M$ là điểm thuộc đoạn $AB$ sao cho $AM = \dfrac{1}{4}AB$

Câu 17 :

Cho hình vuông $MNPQ$ nội tiếp tam giác $ABC$ vuông cân tại $A$ (hình vẽ). Biết ${S_{MNPQ}} = 484c{m^2}.\;$ Tính ${S_{ABC}}$ .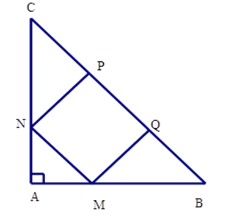

A

$1089c{m^2}$
B

$1809c{m^2}$
C

$\dfrac{{1089}}{2}c{m^2}$
D

$2178c{m^2}$

Cho tam giác $ABC$ có diện tích $12c{m^2}$ . Gọi $N$ là trung điểm của $BC,{\rm{ }}M$ trên $AC$ sao cho $AM = \dfrac{1}{3}AC$ , $AN$ cắt $BM$ tại $O$ .

Câu 18

Chọn câu đúng.

A.

$AO = ON$
B.

$BO = 3OM$
C.

$BO = 2OM$
D.

Cả A, B đều đúng.

Câu 19

Tính diện tích tam giác $AOM$

A.

$4c{m^2}$
B.

$3c{m^2}$
C.

$2c{m^2}$
D.

$1c{m^2}$

Cho tam giác $ABC,\,\,\widehat A = {90^0},\,\,AB = 6cm,\,\,AC = 8cm.$ Hạ $AH \bot BC,$ qua $H$ kẻ $HE \bot AB,\,\,HF \bot AC$ với $E \in AB;F \in AC$ .

Câu 20

Tính $BC$ , $EF.$

A.

$BC = 10cm;EF = 4,8cm$
B.

$BC = 10cm;EF = 2,4cm$
C.

$BC = 5cm;EF = 4,8cm$
D.

$BC = 12cm;EF = 5,4cm$

Câu 21

Gọi $M,\,\,N$ lần lượt là trung điểm của $HB$ và $HC$ . Tính diện tích tứ giác $MNFE$ .

A.

$18c{m^2}$
B.

$6c{m^2}$
C.

$12c{m^2}$
D.

$24c{m^2}$

Cho hình bình hành $ABCD$ có $CD = 4cm$ , đường cao vẽ từ $A$ đến cạnh $CD$ bằng $3cm.$ Gọi $M$ là trung điểm của $AB.$ $DM$ cắt $AC$ tại $N.$

Câu 22

Tính diện tích hình bình hành $ABCD$ , diện tích tam giác $ADM.$

A.

${S_{ABCD}} = 12c{m^2};{S_{ADM}} = 3c{m^2}$
B.

${S_{ABCD}} = 12c{m^2};{S_{ADM}} = 6c{m^2}$
C.

${S_{ABCD}} = 24c{m^2};{S_{ADM}} = 3c{m^2}$
D.

${S_{ABCD}} = 24c{m^2};{S_{ADM}} = 6c{m^2}$

Câu 23

Tính diện tích tam giác $AMN.$

A.

$4c{m^2}$
B.

$10c{m^2}$
C.

$2c{m^2}$
D.

$1c{m^2}$

Câu 24 :

Cho hình bình hành $ABCD$ có $\widehat B = {120^0},AB = 2BC.$ Gọi $I$ là trung điểm của $CD,{\rm{ }}K$ là trung điểm của $AB.$ Biết chu vi hình bình hành $ABCD$ bằng $60cm.$ Tính diện tích hình bình hành $ABCD.$

A

$100\sqrt 3 c{m^2}$
B

$100c{m^2}$
C

$200\sqrt 3 c{m^2}$
D

$200c{m^2}$

Câu 25 :

Tam giác $ABC$ có hai trung tuyến $AM$ và $BN$ vuông góc với nhau. Hãy tính diện tích tam giác đó theo hai cạnh $AM$ và $BN.$

A

${S_{ABC}} = AM.BN$
B

${S_{ABC}} = \dfrac{3}{2}AM.BN$
C

${S_{ABC}} = \dfrac{1}{2}AM.BN$
D

${S_{ABC}} = \dfrac{2}{3}AM.BN$

Lời giải và đáp án

Câu 1 :

Đa giác đều là đa giác

A

Có tất cả các cạnh bằng nhau
B

Có tất cả các góc bằng nhau
C

Có tất cả các cạnh bằng nhau và các góc bằng nhau
D

Cả ba câu trên đều đúng

Đáp án : C

Lời giải chi tiết :

Theo định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và các góc bằng nhau

Câu 2 :

Hãy chọn câu đúng:

A

Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông
B

Diện tích hình chữ nhật bằng nửa tích hai kích thước của nó
C

Diện tích hình vuông có cạnh $a$ là $2a$
D

Tất cả các đáp án trên đều đúng

Đáp án : A

Phương pháp giải :

Dựa vào công thức tính diện tích hình chữ nhật, hình vuông, tam giác vuông

Lời giải chi tiết :

+) Diện tích hình chữ nhật bằng tích hai kích thước của nó.

+) Diện tích hình vuông có cạnh a là ${a^2}.$

+) Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông của tam giác vuông đó.

Câu 3 :

Một đa giác lồi $10$ cạnh thì có số đường chéo là:

A

$35$
B

$30$
C

$70$
D

$27$

Đáp án : A

Phương pháp giải :

Sử dụng công tính tính số đường chéo của hình n cạnh: $\dfrac{{n\left( {n - 3} \right)}}{2}$

Lời giải chi tiết :

Số đường chéo của hình $10$ cạnh là: $\dfrac{{10\left( {10 - 3} \right)}}{2} = 35$ đường.

Câu 4 :

Số đo mỗi góc của hình $9$ cạnh đều là:

A

$120^\circ$
B

$60^\circ$
C

$140^\circ$
D

$135^\circ$

Đáp án : C

Phương pháp giải :

Sử dụng công thức tính số đo góc của đa giác đều n cạnh: $\dfrac{{\left( {n - 2} \right).180^\circ }}{n}$

Lời giải chi tiết :

Số đo góc của đa giác đều 9 cạnh: $\dfrac{{\left( {9 - 2} \right).180^\circ }}{9} = 140^\circ$

Câu 5 :

Một tam giác có độ dài ba cạnh là $12cm,{\rm{ 5}}cm,{\rm{ 13}}cm.$ Diện tích tam giác đó là

A

$60c{m^2}$
B

$30c{m^2}$
C

$45c{m^2}$
D

$32,5c{m^2}$

Đáp án : B

Phương pháp giải :

Với kích thước đã cho chứng minh được tam giác này vuông nên diện tích tam giác bằng một nửa tích hai cạnh góc vuông.

Lời giải chi tiết :

Ta có: ${5^2} + {12^2} = 169;\,{13^2} = 169 \Rightarrow {5^2} + {12^2} = {13^2}$

Do đó đây tam giác đã cho là tam giác vuông có hai cạnh góc vuông là $5cm$ và $12cm.$

Diện tích của nó là: $\dfrac{1}{2}.12.5 = 30\left( {c{m^2}} \right)$

Câu 6 :

Tổng số đo các góc của hình đa giác $n$ cạnh là $900^\circ$ thì

A

$n = 7$
B

$n = 8$
C

$n = 9$
D

$n = 6$

Đáp án : A

Phương pháp giải :

Tổng số đo các góc trong đa giác n cạnh là : $\left( {n - 2} \right){.180^0}$ (với $n \ge 3$ )

Lời giải chi tiết :

Áp dụng công thức tính tổng số đo các góc trong đa giác n cạnh là : $\left( {n - 2} \right){.180^0}$ (với $n \ge 3$ ), ta có:

$\begin{array}{l}\left( {n - 2} \right){.180^0} = 900^\circ \\ \Rightarrow n - 2 = 900^\circ :{180^0}\\ \Rightarrow n - 2 = 5\\ \Rightarrow n = 7\end{array}$

Câu 7 :

Hình chữ nhật có chiều dài tăng 4 lần, chiều rộng giảm 2 lần, khi đó diện tích hình chữ nhật

A

không thay đổi
B

tăng $4$ lần
C

giảm $2$ lần
D

tăng $2$ lần

Đáp án : D

Phương pháp giải :

Sử dụng công thức tính diện tích hình chữ nhật bằng tích chiều dài nhân chiều rộng.

Lời giải chi tiết :

Theo công thức tính diện tích hình chữ nhật $S = a.b$ thì diện tích hình chữ nhật tỉ lệ thuận với chiều dài và chiều rộng của nó

Nếu $a' = 4a;\,\,\,b' = \dfrac{1}{2}b;\,$ thì $S' = a'.b' = 4a.\dfrac{1}{2}b = \dfrac{4}{2}ab = 2S$

Do đó diện tích mới bằng $2$ lần diện tích đã cho.

Câu 8 :

Hình chữ nhật có diện tích là $240c{m^2}$ , chiều rộng là 8cm. Chu vi hình chữ nhật đó là:

A

$38cm$
B

$76cm$
C

$19cm$
D

$152cm$

Đáp án : B

Phương pháp giải :

Tính chiều dài hình chữ nhật từ công thức tính diện tích hình chữ nhật: $S = ab$ , rồi tính chu vi hình chữ nhật theo công thức: $C = 2\left( {a + b} \right)$ .

Lời giải chi tiết :

Chiều dài hình chữ nhật là: $240:8 = 30(cm)$

Chu vi hình chữ nhật là: $2.\left( {30 + 8} \right) = 76(cm)$

Câu 9 :

Cho tam giác $ABC$ với ba đường cao $AA';\,BB';\,CC'$ . Gọi $H$ là trực tâm của tam giác đó. Chọn câu đúng.

A

$\dfrac{{HA'}}{{AA'}} + \dfrac{{HB'}}{{BB'}} + \dfrac{{HC'}}{{CC'}} = 1$
B

$\dfrac{{HA'}}{{AA'}} + \dfrac{{HB'}}{{BB'}} + \dfrac{{HC'}}{{CC'}} = 2$
C

$\dfrac{{HA'}}{{AA'}} + \dfrac{{HB'}}{{BB'}} + \dfrac{{HC'}}{{CC'}} = 3$
D

$\dfrac{{HA'}}{{AA'}} + \dfrac{{HB'}}{{BB'}} + \dfrac{{HC'}}{{CC'}} = 4$

Đáp án : A

Phương pháp giải :

Lập công thức tính diện tích tam giác ABC theo tổng diện tích của ba tam giác HBC; HAC; HAB. Từ đó biến đổi để dẫn đến hệ thức cần tìm.

Lời giải chi tiết :

Ta có:

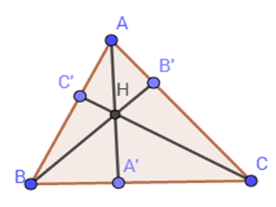$\begin{array}{l}{S_{HBC}} + {S_{HAC}} + {S_{HAB}} = {S_{ABC}}\\ \Rightarrow \dfrac{{{S_{HBC}}}}{{{S_{ABC}}}} + \dfrac{{{S_{HAC}}}}{{{S_{ABC}}}} + \dfrac{{{S_{HAB}}}}{{{S_{ABC}}}} = 1\\ \Leftrightarrow \dfrac{{HA'.BC}}{{AA'.BC}} + \dfrac{{HB'.AC}}{{BB'.AC}} + \dfrac{{HC'.BA}}{{CC'.BA}} = 1\\ \Leftrightarrow \dfrac{{HA'}}{{AA'}} + \dfrac{{HB'}}{{BB'}} + \dfrac{{HC'}}{{CC'}} = 1\,\,\,\,\left( {đpcm} \right).\end{array}$

Câu 10 :

Cho hình thang $ABCD{\rm{ }},{\rm{ }}AB$ song song với $CD,$ đường cao $AH.$ Biết $AB = 7cm;\,CD = 10cm$ , diện tích của $ABCD$ là $25,5c{m^2}$ thì độ dài $AH$ là:

A

2,5cm
B

3cm
C

3,5cm
D

5cm

Đáp án : B

Phương pháp giải :

Từ công thức tính diện tích hình thang bằng nửa tổng hai đáy nhân với đường cao, ta suy ra độ dài đường cao.

Lời giải chi tiết :

Ta có:

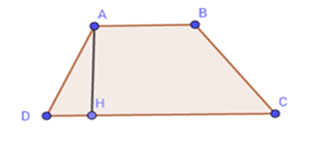$\begin{array}{l}{S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AH}}{2}\\ \Rightarrow AH = \dfrac{{2{S_{ABCD}}}}{{AB + CD}} = \dfrac{{2.25,5}}{{7 + 10}} = 3(cm)\end{array}$

Câu 11 :

Cho hình bình hành $ABCD,$ đường cao ứng với cạnh $DC$ là $AH = 6cm$ ; cạnh $DC = 12cm$ . Diện tích của hình bình hành $ABCD$ là:

A

$72c{m^2}$
B

$82c{m^2}$
C

$92c{m^2}$
D

$102c{m^2}$

Đáp án : A

Phương pháp giải :

Sử dụng công thức tính diện tích hình bình hành bằng tích của một cạnh với chiều cao tương ứng với cạnh đó

Lời giải chi tiết :

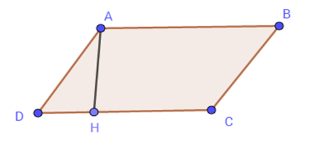Ta có: ${S_{ABCD}} = AH.CD = 6.12 = 72\left( {c{m^2}} \right)$

Câu 12 :

Tính diện tích của tam giác đều $ABC$ biết chu vi tam giác $ABC$ bằng $18cm.$

A

$9\left( {c{m^2}} \right)$
B

$18\sqrt 3 \left( {c{m^2}} \right)$
C

$9\sqrt 3 \left( {c{m^2}} \right)$
D

$27\sqrt 3 \left( {c{m^2}} \right)$

Đáp án : C

Phương pháp giải :

Tính độ dài đường cao hạ từ đỉnh $A.$

Sử dụng công thức tính diện tích tam giác bằng nửa tích chiều cao với cạnh đáy tương ứng.

Lời giải chi tiết :

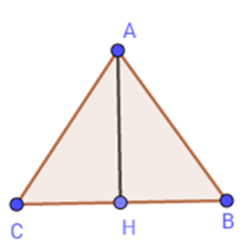Cạnh của tam giác đều là: $AB = BC = CA = 18:3 = 6(cm)$

Gọi $AH$ là đường cao kẻ từ đỉnh $A$ của tam giác $ABC.$

Khi đó $AH$ vừa là đường cao vừa là đường trung tuyến của tam giác đều $ABC.$

Suy ra $BH = HC = \dfrac{1}{2}BC = \dfrac{1}{2}.6 = 3(cm)$

Áp dụng định lí Py-ta-go trong tam giác vuông $AHB$ ta có:

$AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{6^2} - {3^2}} = \sqrt {27} = 3\sqrt 3 (cm)$

Diện tích tam giác đều là: ${S_{ABC}} = \dfrac{{AH.BC}}{2} = \dfrac{{3\sqrt 3 .6}}{2} = 9\sqrt 3 (c{m^2})$

Câu 13 :

Cho hình thoi $ABCD$ có hai đường chéo $AC$ và $BD$ cắt nhau tại $O.$ Biết $OA = 12cm$ , diện tích hình thoi $ABCD$ là $168c{m^2}$ . Cạnh của hình thoi là:

A

$\sqrt {190} (cm)$
B

$\sqrt {180} (cm)$
C

$\sqrt {193} (cm)$
D

$\sqrt {195} (cm)$

Đáp án : C

Phương pháp giải :

Tính $BO$ , áp dụng định lí Py-ta-go trong tam giác vuông $AOB$ để tính cạnh $AB$

Lời giải chi tiết :

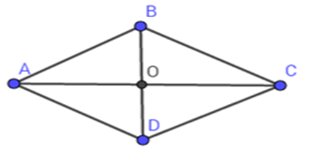Ta có:

$AC = 2AO = 2.12 = 24cm$

$\begin{array}{l}{S_{ABCD}} = \dfrac{1}{2}BD.AC \Rightarrow BD = \dfrac{{2{S_{ABCD}}}}{{AC}} = \dfrac{{2.168}}{{24}} = 14(cm)\\ \Rightarrow BO = \dfrac{1}{2}BD = \dfrac{1}{2}.14 = 7(cm)\end{array}$

Áp dụng định lí Py-ta-go trong tam giác vuông AOB vuông tại O ta có:

$AB = \sqrt {A{O^2} + B{O^2}} = \sqrt {{{12}^2} + {7^2}} = \sqrt {193} (cm)$

Câu 14 :

Cho tam giác $ABC$ trung tuyến $AM,$ chiều cao $AH$ . Chọn câu đúng

A

${S_{ABM}} = {S_{ACM}} = {S_{ABC}}$
B

${S_{ABM}} = {S_{ACM}} = \dfrac{1}{2}{S_{ABC}}$
C

${S_{ABM}} = {S_{ACB}} = \dfrac{1}{2}{S_{AMC}}$
D

${S_{ABM}} = \dfrac{1}{2}{S_{ACM}} = \dfrac{1}{2}{S_{ABC}}$

Đáp án : B

Phương pháp giải :

Sử dụng công thức tính diện tích tam giác: $S = \dfrac{1}{2}ah$ với $a$ là độ dài đáy, $h$ là độ dài chiều cao ứng với đáy.

Lời giải chi tiết :

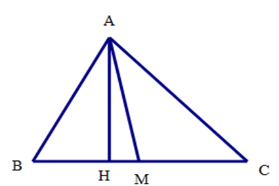Ta có ${S_{ABM}} = \dfrac{1}{2}AH.BM$ ; ${S_{AMC}} = \dfrac{1}{2}AH.MC$ ; ${S_{ABC}} = \dfrac{1}{2}AH.BC$

Mà $M$ là trung điểm của $BC$ nên $MB = MC = \dfrac{{BC}}{2}$

Từ đó ta suy ra ${S_{ABM}} = \dfrac{1}{2}AH.BM = \dfrac{1}{2}AH.CM = \dfrac{1}{2}AH.\dfrac{1}{2}BC = \dfrac{1}{2}\dfrac{{AH.BC}}{2}$

Hay ${S_{ABM}} = {S_{ACM}} = \dfrac{1}{2}{S_{ABC}}$ .

Câu 15 :

Cho hình chữ nhật ABCD có $AD = 8cm,\;AB = 9cm$ . Các điểm $M,{\rm{ }}N$ trên đường chéo $BD$ sao cho $BM = MN = ND.$ Tính diện tích tam giác $CMN.$

A

$12c{m^2}$
B

$24c{m^2}$
C

$36c{m^2}$
D

$6c{m^2}$

Đáp án : A

Phương pháp giải :

+ Tính tỉ số diện tích tam giác $CMN$ và tam giác $BCD$

+ Tính diện tích $\Delta BCD$ suy ra diện tích tam giác $CMN.$

Lời giải chi tiết :

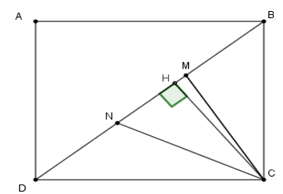+ Ta có $CD = AB = 9cm;BC = AD = 8cm$ nên ${S_{BCD}} = \dfrac{1}{2}BC.DC = \dfrac{1}{2}.8.9 = 36\,c{m^2}$

+ Kẻ $CH \bot BD$ tại $H.$

+ Ta có ${S_{BCD}} = \dfrac{1}{2}CH.BD;{S_{CMN}} = \dfrac{1}{2}CH.MN$ mà $MN = \dfrac{1}{3}BD \Rightarrow {S_{CMN}} = \dfrac{1}{3}{S_{BCD}} = \dfrac{1}{3}.36 = 12\,c{m^2}$

Câu 16 :

Cho hình chữ nhật $ABCD$ . Trên cạnh $AB$ lấy M . Tìm vị trí của M để ${S_{MBC}} = \dfrac{1}{4}{S_{ABCD}}$

A

$M$ là điểm thuộc đoạn $AB$ sao cho $AM = \dfrac{1}{2}MB$
B

$M$ là điểm thuộc đoạn $AB$ sao cho $AM = \dfrac{3}{4}AB$
C

$M$ là trung điểm đoạn $AB.$
D

$M$ là điểm thuộc đoạn $AB$ sao cho $AM = \dfrac{1}{4}AB$

Đáp án : C

Phương pháp giải :

Sử dụng công thức tính diện tích hình chữ nhật và diện tích tam giác vuông.

Lời giải chi tiết :

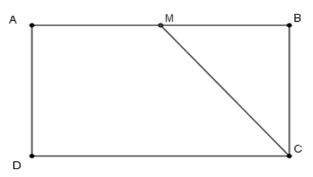Ta có ${S_{ABCD}} = AB.BC$ ; ${S_{MBC}} = \dfrac{1}{2}MB.BC$

Để ${S_{MBC}} = \dfrac{1}{4}{S_{ABCD}} \Leftrightarrow \dfrac{1}{2}MB.BC = \dfrac{1}{4}AB.BC$ $\Leftrightarrow MB = \dfrac{1}{2}AB$

Mà $M \in AB$ nên $M$ là trung điểm đoạn $AB.$

Chú ý

Vì đề bài cho $M$ nằm trên cạnh $AB$ nên ta không xét trường hợp $M$ nằm ngoài đoạn $AB$ .

Câu 17 :

Cho hình vuông $MNPQ$ nội tiếp tam giác $ABC$ vuông cân tại $A$ (hình vẽ). Biết ${S_{MNPQ}} = 484c{m^2}.\;$ Tính ${S_{ABC}}$ .

A

$1089c{m^2}$
B

$1809c{m^2}$
C

$\dfrac{{1089}}{2}c{m^2}$
D

$2178c{m^2}$

Đáp án : A

Phương pháp giải :

+ Sử dụng công thức tính diện tích hình vuông để tính các cạnh của hình vuông $MNPQ$

+Chứng minh các tam giác $CPN;QMB$ vuông cân

+ Kẻ $AH \bot BC$

+ Tính cạnh $BC;AH$ rồi tính diện tích tam giác $ABC.$

Lời giải chi tiết :

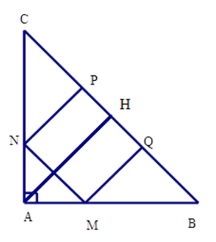Ta có

Kẻ $AH \bot BC \Rightarrow H$ là trung điểm cạnh $BC$ (vì tam giác $ABC$ vuông cân tại $A$ )

Khi đó $AH$ là đường trung tuyến nên $AH = \dfrac{{BC}}{2}$ (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)

+ Xét tam giác vuông $CNP$ có $\widehat C = 45^\circ$ (do tam giác $ABC$ vuông cân) nên tam giác $CNP$ vuông cân tại $P.$ Suy ra $CP = PN = 22cm$

+ Tương tự ta có $\Delta QMB$ vuông cân tại $Q \Rightarrow QM = QB = 22cm$

Từ đó $BC = PC + PQ + QB = 22 + 22 + 22 = 66cm$

Mà $AH = \dfrac{{BC}}{2}\left( {cmt} \right) \Rightarrow AH = \dfrac{{66}}{2} = 33cm$

Từ đó ${S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.33.66 = 1089\,c{m^2}$

Chú ý

Các em có thể tính các cạnh $AB;AC$ rồi tính ${S_{ABC}} = \dfrac{{AB.AC}}{2}$

Cho tam giác $ABC$ có diện tích $12c{m^2}$ . Gọi $N$ là trung điểm của $BC,{\rm{ }}M$ trên $AC$ sao cho $AM = \dfrac{1}{3}AC$ , $AN$ cắt $BM$ tại $O$ .

Câu 18

Chọn câu đúng.

A.

$AO = ON$
B.

$BO = 3OM$
C.

$BO = 2OM$
D.

Cả A, B đều đúng.

Đáp án : D

Phương pháp giải :

+) Sử dụng tính chất của đường trung bình trong tam giác.

+) Sử dụng tỉ lệ của diện tích các tam giác.

Lời giải chi tiết :

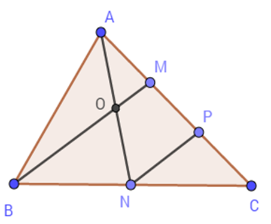Lấy $P$ là trung điểm của $CM.$ Vì $AM = \dfrac{1}{3}AC \Rightarrow MC = \dfrac{2}{3}AC$ $\Rightarrow MP = PC = \dfrac{1}{3}AC = AM$

Tam giác $BCM$ có: $\left\{ \begin{array}{l}NB = NC\,\,(gt)\\PC = PM\,\,(gt)\end{array} \right.$

Suy ra $NP$ là đường trung bình của tam giác $BMC$ (định nghĩa).

Suy ra $NP//BM$ (tính chất đường trung bình).

Tam giác ANP có $\left\{ \begin{array}{l}MA = MP\,\,\,(cmt)\\OM//NP\,\,\,(do\,\,NP//BM)\end{array} \right.$

$\Rightarrow AO = ON$ (định lý đảo của đường trung bình).

Theo chứng minh trên ta có OM là đường trung bình của tam giác ANP nên $OM = \dfrac{1}{2}NP\,\,\,\,(1)$

NP là đường trung bình của tam giác BCM nên $NP = \dfrac{1}{2}BM\,\,\,(2)$

Từ (1) và (2) suy ra $BM = 4OM \Rightarrow BO = 3OM$ .

Vậy cả A, B đều đúng.

Câu 19

Tính diện tích tam giác $AOM$

A.

$4c{m^2}$
B.

$3c{m^2}$
C.

$2c{m^2}$
D.

$1c{m^2}$

Đáp án : D

Phương pháp giải :

+) Sử dụng công thức tính diện tích tam giác và tỉ lệ của diện tích các tam giác.

Lời giải chi tiết :

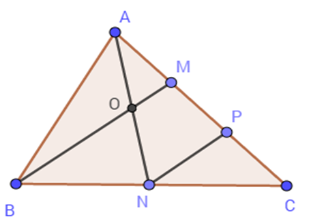Hai tam giác $AOM$ và $ABM$ có chung đường cao hạ từ $A$ nên $\dfrac{{{S_{AOM}}}}{{{S_{ABM}}}} = \dfrac{{OM}}{{BM}}$ $= \dfrac{1}{4} \Rightarrow {S_{AOM}} = \dfrac{1}{4}{S_{ABM}}$

Hai tam giác $ABM$ và $ABC$ có chung đường cao hạ từ $B$ nên $\dfrac{{{S_{ABM}}}}{{{S_{ABC}}}} = \dfrac{{AM}}{{AC}} = \dfrac{1}{3}$ $\Rightarrow {S_{ABM}} = \dfrac{1}{3}{S_{ABC}}$

Vậy ${S_{AOM}} = \dfrac{1}{4}.\dfrac{1}{3}.12 = 1\left( {c{m^2}} \right)$

Cho tam giác $ABC,\,\,\widehat A = {90^0},\,\,AB = 6cm,\,\,AC = 8cm.$ Hạ $AH \bot BC,$ qua $H$ kẻ $HE \bot AB,\,\,HF \bot AC$ với $E \in AB;F \in AC$ .

Câu 20

Tính $BC$ , $EF.$

A.

$BC = 10cm;EF = 4,8cm$
B.

$BC = 10cm;EF = 2,4cm$
C.

$BC = 5cm;EF = 4,8cm$
D.

$BC = 12cm;EF = 5,4cm$

Đáp án : A

Phương pháp giải :

+) Sử dụng định lý Pi-ta-go để tính độ dài cạnh huyền $BC.$

+) Áp dụng định lý Pi-ta-go với các tam giác vuông $AHC$ và $BHC$ để tính cạnh $AH.$

+) Chứng minh tứ giác $AEHF$ là hình chữ nhật, từ đó suy ra hai đường chéo $AH = EF.$

Lời giải chi tiết :

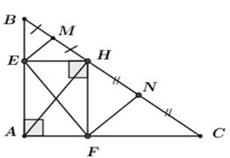Áp dụng định lý Pi-ta-go trong tam giác $ABC$ vuông tại $A$ ta có:

$BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{6^2} + {8^2}} = \sqrt {100} = 10\,cm.$

Áp dụng định lý Pi-ta-go trong tam giác $ABH$ vuông tại $H$ ta có:

$A{H^2} = A{B^2} - B{H^2} = 36 - B{H^2}.$

Áp dụng định lý Pi-ta-go trong tam giác $ACH$ vuông tại $H$ ta có:

$\begin{array}{l}A{H^2} = A{C^2} - H{C^2} = 64 - H{C^2}.\\ \Rightarrow 36 - B{H^2} = 64 - H{C^2}\\ \Leftrightarrow 36 - B{H^2} = 64 - {\left( {10 - BH} \right)^2}\\\left( {do\,\,\,HC + BH = BC = 10} \right)\\ \Leftrightarrow 28 - 100 + 20BH - B{H^2} + B{H^2} = 0\\ \Leftrightarrow 20BH = 72\\ \Leftrightarrow BH = 3,6\,\,\,cm.\\ \Rightarrow AH = \sqrt {36 - B{H^2}} = \sqrt {36 - 3,{6^2}} = 4,8\,\,cm.\end{array}$

Xét tứ giác $AEHF$ có: $\widehat A = \widehat E = \widehat F = {90^0}\,\,\,\left( {gt} \right)$

$\Rightarrow AEHF$ là hình chữ nhật (dhnb) $\Rightarrow AH = EF\,\,\,$ (hai đường chéo hình chữ nhật bằng nhau).

$\Rightarrow EF = AH = 4,8\,\,cm.$

Câu 21

Gọi $M,\,\,N$ lần lượt là trung điểm của $HB$ và $HC$ . Tính diện tích tứ giác $MNFE$ .

A.

$18c{m^2}$
B.

$6c{m^2}$
C.

$12c{m^2}$
D.

$24c{m^2}$

Đáp án : C

Phương pháp giải :

+) Tính diện tích theo mối quan hệ ${S_{MNFE}} = {S_{\Delta MEH}} + {S_{\Delta HEF}} + {S_{\Delta NFH}}$

Lời giải chi tiết :

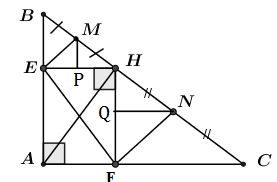Kẻ $MP \bot EH\,\,\left( {P \in EH} \right),\,\,NQ \bot HF\,\,\left( {Q \in HF} \right)$ ta có: MP và NQ lần lượt là đường trung bình của tam giác HBE và HFC nên $MP = \dfrac{1}{2}BE,\,\,NQ = \dfrac{1}{2}FC$

$\begin{array}{l}{S_{\Delta MEH}} = \dfrac{1}{2}MP.EH = \dfrac{1}{2}.\dfrac{1}{2}BE.EH = \dfrac{1}{2}{S_{\Delta HBE}}\\{S_{\Delta HNF}} = \dfrac{1}{2}NQ.HF = \dfrac{1}{2}.\dfrac{1}{2}CF.HF = \dfrac{1}{2}{S_{\Delta HCF}}\\{S_{\Delta H{\rm{EF}}}} = \dfrac{1}{2}{S_{AEHF}}\\ \Rightarrow {S_{EMNF}} = \dfrac{1}{2}\left( {{S_{\Delta HBE}} + {S_{\Delta HCF}} + {S_{AEHF}}} \right) \\= \dfrac{1}{2}{S_{\Delta ABC}} = \dfrac{1}{2}\,.\dfrac{1}{2}.AB.AC = \dfrac{1}{4}.6.8 = 12\,\,\left( {c{m^2}} \right).\end{array}$

Chú ý

Các em cũng có thể tính diện tích theo mối quan hệ ${S_{MNFE}} = {S_{\Delta ABC}} - {S_{\Delta MBE}} - {S_{\Delta NCF}} - {S_{\Delta AEF}}$

Cho hình bình hành $ABCD$ có $CD = 4cm$ , đường cao vẽ từ $A$ đến cạnh $CD$ bằng $3cm.$ Gọi $M$ là trung điểm của $AB.$ $DM$ cắt $AC$ tại $N.$

Câu 22

Tính diện tích hình bình hành $ABCD$ , diện tích tam giác $ADM.$

A.

${S_{ABCD}} = 12c{m^2};{S_{ADM}} = 3c{m^2}$
B.

${S_{ABCD}} = 12c{m^2};{S_{ADM}} = 6c{m^2}$
C.

${S_{ABCD}} = 24c{m^2};{S_{ADM}} = 3c{m^2}$
D.

${S_{ABCD}} = 24c{m^2};{S_{ADM}} = 6c{m^2}$

Đáp án : A

Phương pháp giải :

Sử dụng công thức tính diện tích hình bình hành bằng tích chiều cao với đáy, diện tích tam giác bằng nửa tích chiều cao với cạnh đáy tương ứng.

Lời giải chi tiết :

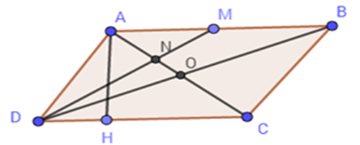+) ${S_{ABCD}} = AH.CD = 4.3 = 12\left( {c{m^2}} \right)$

+) Vì $M$ là trung điểm của $AB$ nên $AM = \dfrac{1}{2}AB = \dfrac{1}{2}.4 = 2(cm)$

Ta có chiều cao từ đỉnh $D$ đến cạnh $AM$ của tam giác $ADM$ bằng chiều cao $AH$ của hình bình hành.

$\Rightarrow {S_{ADM}} = \dfrac{1}{2}AH.AM = \dfrac{1}{2}.3.2 = 3\left( {c{m^2}} \right)$

Câu 23

Tính diện tích tam giác $AMN.$

A.

$4c{m^2}$
B.

$10c{m^2}$
C.

$2c{m^2}$
D.

$1c{m^2}$

Đáp án : D

Phương pháp giải :

+ Sử dụng tính chất đường trung tuyến của tam giác.

+ Chỉ ra rằng $NM = \dfrac{{DM}}{3}$ .

+ Tính diện tích tam giác $AMN$ dựa vào diện tích tam giác $ADM.$

Lời giải chi tiết :

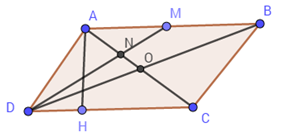Tứ giác $ABCD$ là hình bình hành nên $AC$ và $BD$ cắt nhau tại trung điểm $O$ của mỗi đường.

Xét tam giác $ABD$ ta có: $AO$ và $DM$ là hai đường trung tuyến của tam giác.

Mà $AO \cap DM = \left\{ N \right\} \Rightarrow$ $N$ là trọng tâm tam giác $ADB.$

$\Rightarrow AN = \dfrac{2}{3}DM$ (tính chất đường trung tuyến của tam giác)

Suy ra $NM = \dfrac{{DM}}{3}$ .

+) Hai tam giác $AMN$ và $ADM$ có cùng đường cao hạ từ A nên $\dfrac{{{S_{AMN}}}}{{{S_{ADM}}}} = \dfrac{{MN}}{{DM}} = \dfrac{1}{3}$

Mà theo câu trước ${S_{\Delta ADM}} = 3\,c{m^2}$

$\Rightarrow {S_{AMN}} = \dfrac{1}{3}{S_{ADM}} = \dfrac{1}{3}.3 = 1\left( {c{m^2}} \right)$

Câu 24 :

A

$100\sqrt 3 c{m^2}$
B

$100c{m^2}$
C

$200\sqrt 3 c{m^2}$
D

$200c{m^2}$

Đáp án : A

Phương pháp giải :

+) Kẻ $BH$ là đường cao ứng với cạnh $CD$ của hình bình hành $ABCD$ $\Rightarrow {S_{ABCD}} = BH.CD.$

Lời giải chi tiết :

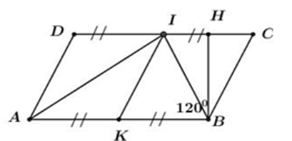Kẻ $BH$ là đường cao ứng với cạnh $CD$ của hình bình hành $ABCD$ $\Rightarrow {S_{ABCD}} = BH.CD.$

Theo đề bài ta có chu vi hình bình hành $ABCD$ bằng $60cm.$

$\Rightarrow 2\left( {AB + BC} \right) = 60 \Leftrightarrow 2.3BC = 60 \Leftrightarrow BC = 10cm.$

Xét tứ giác $KICB$ ta có: $IC = BC = KB = IK = \dfrac{1}{2}AB=10cm$

$\Rightarrow IKBC$ là hình thoi. (dấu hiệu nhận biết).

Mà $\widehat B = {120^0} \Rightarrow \widehat {ICB} = {180^0} - {120^0} = {60^0}.$

Xét tam giác ICB có: $\left\{ \begin{array}{l}IC = BC\\\widehat {ICB} = {60^0}\end{array} \right. \Rightarrow ICB$ là tam giác đều. (tam giác cân có góc ở đỉnh bằng ${60^0}$ ).

$\Rightarrow BH$ vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.

$\Rightarrow HI = HC = \dfrac{1}{2}BC = 5cm.$

Áp dụng định lý Pi-ta-go với tam giác vuông HBC ta có:

$BH = \sqrt {B{C^2} - H{C^2}} = \sqrt {{{10}^2} - {5^2}} = \sqrt {75} = 5\sqrt 3 \,cm.$

$\Rightarrow {S_{ABCD}} = BH.AB = BH.2BC = 5\sqrt 3 .2.10 = 100\sqrt 3 c{m^2}.$

Câu 25 :

Tam giác $ABC$ có hai trung tuyến $AM$ và $BN$ vuông góc với nhau. Hãy tính diện tích tam giác đó theo hai cạnh $AM$ và $BN.$

A

${S_{ABC}} = AM.BN$
B

${S_{ABC}} = \dfrac{3}{2}AM.BN$
C

${S_{ABC}} = \dfrac{1}{2}AM.BN$
D

${S_{ABC}} = \dfrac{2}{3}AM.BN$

Đáp án : D

Phương pháp giải :

$ABMN$ là tứ giác có hai đường chéo $AM$ và $BN$ vuông góc nên có diện tích bằng nửa tích hai đường chéo

Tính diện tích tam giác $ABC$ thông qua diện tích của tứ giác $ABMN$

Lời giải chi tiết :

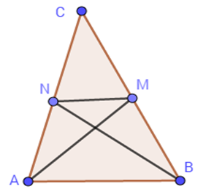Ta có $ABMN$ là tứ giác có hai đường chéo $AM$ và $BN$ vuông góc nên có diện tích là: ${S_{ABMN}} = \dfrac{1}{2}AB.MN$

Hai tam giác $AMC$ và $ABC$ có chung đường cao hạ từ $A$ nên $\dfrac{{{S_{AMC}}}}{{{S_{ABC}}}} = \dfrac{{MC}}{{BC}} = \dfrac{1}{2}$ $\Rightarrow {S_{AMC}} = \dfrac{1}{2}{S_{ABC}}\,(1)$

Hai tam giác $AMN$ và $AMC$ có chung đường cao hạ từ $M$ nên $\dfrac{{{S_{AMN}}}}{{{S_{AMC}}}} = \dfrac{{AN}}{{AC}} = \dfrac{1}{2}$ $\Rightarrow {S_{AMN}} = \dfrac{1}{2}{S_{AMC}}\,(2)$

Từ (1) và (2) suy ra ${S_{AMN}} = \dfrac{1}{4}{S_{ABC}}\,$

Hai tam giác $AMB$ và $ABC$ có chung đường cao hạ từ $A$ nên $\dfrac{{{S_{AMB}}}}{{{S_{ABC}}}} = \dfrac{{MB}}{{BC}} = \dfrac{1}{2}$ $\Rightarrow {S_{AMB}} = \dfrac{1}{2}{S_{ABC}}\,$

Ta có: ${S_{ABMN}} = {S_{AMN}} + {S_{ABM}} = \dfrac{1}{4}{S_{ABC}} + \dfrac{1}{2}{S_{ABC}} = \dfrac{3}{4}{S_{ABC}}$

$\Rightarrow {S_{ABC}} = \dfrac{4}{3}{S_{ABMN}} = \dfrac{4}{3}.\dfrac{1}{2}.AM.BN = \dfrac{2}{3}AM.BN$

Bài liên quan

Trắc nghiệm Bài 4,5: Diện tích hình thang, diện tích hình thoi Toán 8

Luyện tập và củng cố kiến thức Bài 4,5: Diện tích hình thang, diện tích hình thoi Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 2,3: Diện tích hình chữ nhật, diện tích tam giác Toán 8

Luyện tập và củng cố kiến thức Bài 2,3: Diện tích hình chữ nhật, diện tích tam giác Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 1: Đa giác, đa giác đều Toán 8

Luyện tập và củng cố kiến thức Bài 1: Đa giác, đa giác đều Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Trắc nghiệm Bài tập ôn tập chương 6 Toán 8

Trắc nghiệm Bài 4,5: Diện tích hình thang, diện tích hình thoi Toán 8

Trắc nghiệm Bài 2,3: Diện tích hình chữ nhật, diện tích tam giác Toán 8

Trắc nghiệm Bài 1: Đa giác, đa giác đều Toán 8