Trắc nghiệm Bài 1: Tứ giác Toán 8Đề bài
Câu 1 :
Hãy chọn câu sai.
Câu 2 :
Cho hình vẽ dưới đây. Chọn khẳng định sai. 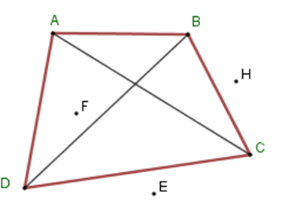
Câu 3 :
Cho hình vẽ sau. Chọn câu sai. 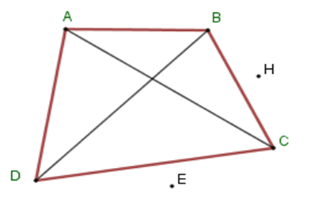
Câu 4 :
Cho tứ giác ABCD có ˆA=600;ˆB=1350;ˆD=290 . Số đo góc C bằng:
Câu 5 :
Cho tứ giác ABCD có ˆA=500;ˆC=1500;ˆD=450. Số đo góc ngoài tại đỉnh B bằng:
Câu 6 :
Cho tứ giác ABCD . Tổng số đo các góc ngoài tại 4 đỉnh A,B,C,D là
Câu 7 :
Cho tứ giác ABCD có ˆA=100∘ . Tổng số đo các góc ngoài đỉnh B,C,D bằng:
Câu 8 :
Tứ giác ABCD có AB=BC,CD=DA,ˆB=900;ˆD=1200. Hãy chọn câu đúng nhất:
Câu 9 :
Cho tứ giácABCD. Gọi O là giao điểm của hai đường chéo AC vàBD . Khẳng định nào sau đây là đúng nhất.
Câu 10 :
Cho tứ giác ABCD biết số đo của các góc ˆA;ˆB;ˆC;ˆD tỉ lệ thuận với 4;3;5;6. Khi đó số đo các góc ˆA;ˆB;ˆC;ˆD lần lượt là:
Câu 11 :
Tam giác ABC có ˆA=60∘, các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc ^BIC;^BKC.
Câu 12 :
Tứ giác ABCD có ˆC+ˆD=90∘. Chọn câu đúng.
Câu 13 :
Tứ giác ABCD có ˆA−ˆC=60∘. Các tia phân giác của các góc B và D cắt nhau tại I. Tính số đo góc BID.
Lời giải và đáp án
Câu 1 :
Hãy chọn câu sai.
Đáp án : B Lời giải chi tiết :
Định lý: Tổng các góc của một tứ giác bằng 3600 nên C đúng, B sai.
Câu 2 :
Cho hình vẽ dưới đây. Chọn khẳng định sai. 
Đáp án : D Phương pháp giải :
Ta sử dụng kiến thức về các yếu tố góc, đỉnh, cạnh của tứ giác ABCD. Lời giải chi tiết :
Từ hình vẽ ta thấy các điểm E,H nằm bên ngoài tứ giác và điểm F nằm bên trong tứ giácABCD nên D sai.
Câu 3 :
Cho hình vẽ sau. Chọn câu sai. 
Đáp án : C Phương pháp giải :
Ta sử dụng kiến thức về các yếu tố góc, đỉnh, cạnh của tứ giác ABCD. Lời giải chi tiết :
Tứ giác ABCD có các cặp góc đối nhau là ˆA;ˆC và ˆB;ˆD còn ˆA;ˆB là hai góc kề nhau nên C sai.
Câu 4 :
Cho tứ giác ABCD có ˆA=600;ˆB=1350;ˆD=290 . Số đo góc C bằng:
Đáp án : B Phương pháp giải :
Ta sử dụng định lý về tổng các góc trong tứ giác. Định lý: Tổng các góc của một tứ giác bằng 360∘ . Lời giải chi tiết :
Xét tứ giác ABCD có ˆA+ˆB+ˆC+ˆD=360∘(định lý) hay 60∘+135∘+ˆC+29∘=360∘⇒ˆC=360∘−60∘−135∘−29∘ ⇔ˆC=136∘ .
Câu 5 :
Cho tứ giác ABCD có ˆA=500;ˆC=1500;ˆD=450. Số đo góc ngoài tại đỉnh B bằng:
Đáp án : A Phương pháp giải :
+ Ta sử dụng định lý về tổng các góc trong tứ giác: Tổng các góc của một tứ giác bằng 360∘ để tính góc B + Từ đó suy ra số đo góc ngoài tại B là 180∘−ˆB . Lời giải chi tiết :
Xét tứ giác ABCD có ˆA+ˆB+ˆC+ˆD=360∘ (định lý) Hay 50∘+ˆB+150∘+45∘=360∘ ˆB=360∘−50∘−150∘−45∘ Nên góc ngoài tại đỉnh B có số đo là 180∘−ˆB=180∘−115∘=65∘ . Chú ý
Một số em khi tính ra góc B đã chọn luôn đáp án D mà không đọc kĩ đề bài hỏi góc ngoài nên chọn sai.
Câu 6 :
Cho tứ giác ABCD . Tổng số đo các góc ngoài tại 4 đỉnh A,B,C,D là
Đáp án : D Phương pháp giải :
Ta sử dụng định nghĩa: Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác. Và định lý: Tổng bốn góc của một tứ giác bằng 3600 . Lời giải chi tiết :
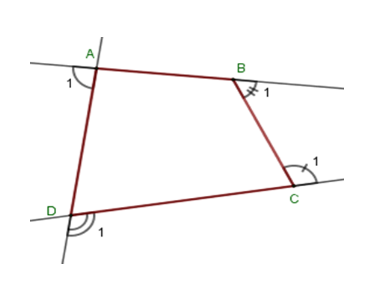 Gọi góc ngoài tại bốn đỉnh A,B,C,D của tứ giác ABCD lần lượt là ^A1;^B1;^C1;^D1 . Khi đó ta có ˆA+^A1=180∘⇒^A1=180∘−ˆA; ˆB+^B1=180∘⇒^B1=180∘−ˆB; ˆC+^C1=180∘⇒^C1=180∘−ˆC và ˆD+^D1=180∘⇒^D1=180∘−ˆD Suy ra ^A1+^B1+^C1+^D1=180∘−ˆA+180∘−ˆB+180∘−ˆC+180∘−ˆD =720∘−(ˆA+ˆB+ˆC+ˆD)=720∘−360∘=360∘ (Vì ˆA+ˆB+ˆC+ˆD=360∘) Vậy tổng số đo các góc ngoài tại 4 đỉnh A,B,C,D là 360∘ .
Câu 7 :
Cho tứ giác ABCD có ˆA=100∘ . Tổng số đo các góc ngoài đỉnh B,C,D bằng:
Đáp án : C Phương pháp giải :
Bước 1: Tính góc ngoài tại đỉnh A Bước 2: Từ các câu trước ta suy ra “ tổng số đo góc ngoài tại bốn đỉnh của một tứ giác là 360∘” . Từ đó tính tổng số đo các góc ngoài đỉnh B,C,D Lời giải chi tiết :
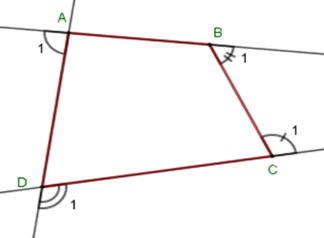 Gọi góc ngoài tại bốn đỉnh A,B,C,D của tứ giác ABCD lần lượt là ^A1;^B1;^C1;^D1 . Khi đó ta có ˆA+^A1=180∘⇒^A1=180∘−ˆA=180∘−100∘=80∘. Theo kết quả các câu trước ta có ^A1+^B1+^C1+^D1=360∘⇒^B1+^C1+^D1=360∘−^A1=360∘−80∘=280∘ . Vậy ^B1+^C1+^D1=280∘. Chú ý
Một số em lấy luôn 360∘−ˆA là sai do ta phải tính góc ngoài tại đỉnh A trước.
Câu 8 :
Tứ giác ABCD có AB=BC,CD=DA,ˆB=900;ˆD=1200. Hãy chọn câu đúng nhất:
Đáp án : D Phương pháp giải :
Ta sử dụng tính chất tam giác vuông cân , tam giác cân và tổng ba góc trong tam giác bằng 180∘ . Lời giải chi tiết :
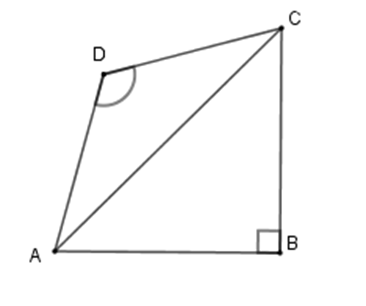 Xét tam giác ABC có ˆB=90∘;AB=BC⇒ΔABC vuông cân ⇒^BAC=^BCA=90∘2=45∘ Xét tam giác ADC có CD=DA⇒ΔADC cân tại D có ^ADC=120∘ nên ^DAC=^DCA=180∘−120∘2=30∘ Từ đó ta có ˆA=^BAD=^BAC+^CAD=45∘+30∘=75∘ Và ˆC=^BCD=^BCA+^ACD=45∘+30∘=75∘ Nên ˆA=ˆC=75∘ . Chú ý
Khi tìm được góc ^BAD các em có thể dùng định lý tổng bốn góc trong tứ giác để tính góc C còn lại.
Câu 9 :
Cho tứ giácABCD. Gọi O là giao điểm của hai đường chéo AC vàBD . Khẳng định nào sau đây là đúng nhất.
Đáp án : C Phương pháp giải :
Ta sử dụng : “ Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.” Lời giải chi tiết :
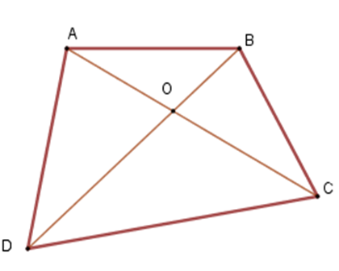 + Xét tam giác OAB ta có OA+OB>AB(vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại) . Tương tự ta có OC+OD>CD;OB+OC>BC;OA+OD>AD Cộng vế với vế ta được OA+OB+OC+OD+OB+OC+OA+OD>AB+BC+CD+AD ⇔2(OA+OB+OC+OD)>AB+BC+CD+DA ⇔OA+OB+OC+OD>AB+BC+CD+DA2 nên B đúng. + Xét tam giác ABC ta có AB+BC>AC (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại) . Tương tự ta có BC+CD>BD;CD+DA>AC;AD+DB>BD Cộng vế với vế ta được: AB+BC+BC+CD+CD+DA+DA+AB>AC+BD+AC+BD ⇔2(AB+BC+CD+DA)>2(AC+BD) ⇔AB+BC+CD+DA>AC+BD mà AC+BD=OA+OC+OB+OD nên AB+BC+CD+DA>OA+OB+OC+OD nên A đúng. Vậy cả A, B đều đúng.
Câu 10 :
Cho tứ giác ABCD biết số đo của các góc ˆA;ˆB;ˆC;ˆD tỉ lệ thuận với 4;3;5;6. Khi đó số đo các góc ˆA;ˆB;ˆC;ˆD lần lượt là:
Đáp án : A Phương pháp giải :
Ta sử dụng tính chất tỉ lệ thức AB=CD=A+CB+D và định lý về tổng các góc trong tứ giác bằng 360∘ . Lời giải chi tiết :
Vì số đo của các góc ˆA;ˆB;ˆC;ˆD tỉ lệ thuận với 4;3;5;6 nên ta có ˆA4=ˆB3=ˆC5=ˆD6=ˆA+ˆB+ˆC+ˆD4+3+5+6=ˆA+ˆB+ˆC+ˆD18 (tính chất dãy tỉ số bằng nhau) Mà ˆA+ˆB+ˆC+ˆD=360∘ nên ta có ˆA4=ˆB3=ˆC5=ˆD6=ˆA+ˆB+ˆC+ˆD18=360∘18=20∘ ⇒ˆA=4.20∘=80∘ ; ˆB=3.20∘=60∘;ˆC=5.20∘=100∘;ˆD=6.20∘=120∘ Nên số đo góc ˆA;ˆB;ˆC;ˆD lần lượt là 80∘;60∘;100∘;120∘ . Chú ý
Một số em sử dụng sai tỉ lệ thức và tính chất dãy tỉ số bằng nhau dẫn đến không ra đáp án đúng.
Câu 11 :
Tam giác ABC có ˆA=60∘, các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc ^BIC;^BKC.
Đáp án : D Phương pháp giải :
+ Sử dụng tính chất tia phân giác của một góc + Định lý: Tổng ba góc trong tam giác bằng 180∘ + Định lý: Tổng bốn góc trong tứ giác bằng 360∘ Lời giải chi tiết :
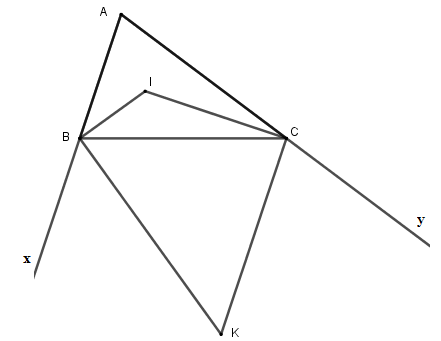 Xét tam giác ABC có: ˆA+^ABC+^BCA=180∘⇔^ABC+^BCA=120∘. Vì BI là phân giác ^BAC⇒^CBI=12^BAC. Vì CI là phân giác ^BCA⇒^BCI=12^BCA. Từ đó: ^CBI+^BCI=12(^BAC+^BCA)=12.120∘=60∘. Xét tam giác BCI có: ^BCI+^BIC+^CBI=180∘ nên ^BIC=180∘−(^BCI+^CBI)=180∘−60∘=120∘. Vì BI là phân giác ^BAC⇒^CBI=12^BAC. Vì BK là phân giác ^CBx⇒^CKB=12^CBx. Suy ra: ^CBK+^CBI=12(^CBx+^ABC)=12.180∘=90∘ hay ^IBK=90∘. Tương tự ta có: ^ICK=90∘. Xét tứ giác BICK có: ^BIC+^IBC+^ICK+^BKC=360∘⇔^BKC=360∘−90∘−90∘−120∘=60∘. Vậy ^BIC=120∘;^BKC=60∘.
Câu 12 :
Tứ giác ABCD có ˆC+ˆD=90∘. Chọn câu đúng.
Đáp án : B Phương pháp giải :
+ Gọi giao điểm của AD và BC là K. + Sử dụng định lý Pytago. Lời giải chi tiết :
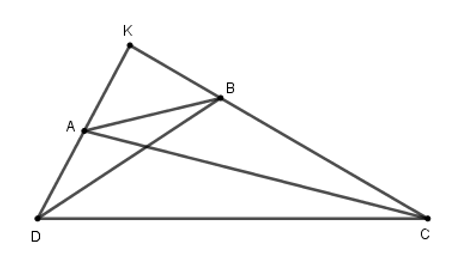 Gọi K là giao điểm AD,BC. Vì ˆC+ˆD=90∘ nên ˆK=90∘. Xét ΔKAC vuông tại K ta có: AC2=KC2+KA2. Xét ΔKBD vuông tại K có: BD2=KB2+KD2. Xét ΔKBA vuông tại K có: BA2=KA2+KB2. Xét ΔKCD vuông tại K có: CD2=KC2+KD2. Từ đó BD2+AC2=KC2+KA2+KB2+KD2=(KB2+KA2)+(KD2+KC2)=AB2+DC2
Câu 13 :
Tứ giác ABCD có ˆA−ˆC=60∘. Các tia phân giác của các góc B và D cắt nhau tại I. Tính số đo góc BID.
Đáp án : A Phương pháp giải :
Sử dụng: Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó. Sử dụng: Tổng bốn góc trong tứ giác bằng 360∘. Lời giải chi tiết :
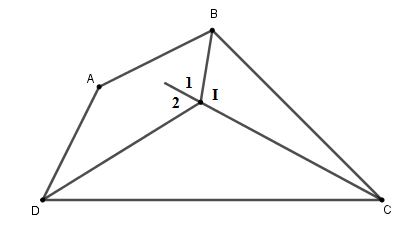 Xét tam giác BIC có: ^IBC=^I1−^BCI. Xét tam giác DIC có: ^IDC=^I2−^ICD. Nên ^IBC+^IDC=(^I1+^I2)−(^C1+^C2)=^BID−ˆC. Tứ giác ABID có: ^ABI+^ADI=360∘−ˆA−^BID. Do ^ABI=^IBC;^ADI=^IDC (tính chất tia phân giác) nên ^IBC+^IDC=^ABI+^ADI. Hay ^BID−ˆC=360∘−ˆA−^BID⇔2^BID=360∘−(ˆA−ˆC)=360∘−60∘=300∘. Suy ra ^BID=150∘.
|












