Trắc nghiệm Bài 7: Hình bình hành Toán 8Đề bài
Câu 1 :
Hãy chọn câu sai:
Câu 2 :
Hãy chọn câu đúng. Tứ giác $ABCD$ là hình bình hành nếu.
Câu 3 :
Hãy chọn câu đúng. Cho hình bình hành $ABCD$ có các điều kiện như hình vẽ, trong hình có: 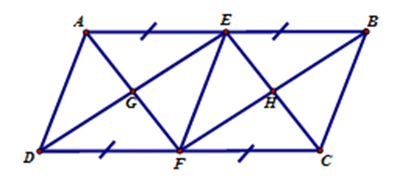
Câu 4 :
Cho hình bình hành $ABCD$ có \(\widehat A = 3\widehat B\) . Số đo các góc của hình bình hành là:
Câu 5 :
Tính số đo các góc của hình bình hành $ABCD$ biết \(\widehat D - \widehat C = {30^0}\). Ta được:
Câu 6 :
Hãy chọn câu trả lời sai. Cho hình vẽ, ta có: 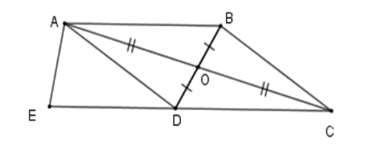
Câu 7 :
Tỉ số độ dài hai cạnh của hình bình hành là \(3:5\). Còn chu vi của nó bằng \(48cm\). Độ dài hai cạnh kề của hình bình hành là:
Câu 8 :
Hai góc kề nhau của một hình bình hành không thể có số đo là:
Cho tam giác $ABC$ và $H$ là trực tâm. Các đường thẳng vuông góc với $AB$ tại $B$ , vuông góc với $AC$ tại $C$ cắt nhau ở $ D$ . Câu 9
Chọn câu trả lời đúng nhất. Tứ giác $BDCH$ là hình gì?
Câu 10
Tính số đo góc \(BDC\) , biết $\widehat {BAC} = 50^\circ $.
Câu 11 :
Cho tứ giác $ABCD$ . Gọi$E$ , $F$ lần lượt là giao điểm của $AB$ và $CD$ , $AD$ và $BC;$ $M,N,P,Q$ lần lượt là trung điểm của $AE$ , $EC$ , $CF$ ,$FA$ . Khi đó \(MNPQ\) là hình gì? Chọn đáp án đúng nhất.
Câu 12 :
Hãy chọn câu sai.
Câu 13 :
Cho hình bình hành $ABCD$ . Gọi $I,{\rm{ }}K$ theo thứ tự là trung điểm của $CD,{\rm{ }}AB$ . Đường chéo $BD$ cắt $AI,{\rm{ }}CK$ theo thứ tự ở $E,{\rm{ }}F$ . Chọn khẳng định đúng.
Câu 14 :
Cho hình bình hành $ABCD$ . Trên đường chéo $BD$ lấy hai điểm $E$ và $F$ sao cho \(BE = DF < \dfrac{1}{2}BD\) . Chọn khẳng định đúng.
Câu 15 :
Cho hình bình hành $ABCD$ có \(\widehat A = \alpha > 90^\circ \) . Ở phía ngoài hình bình hành vẽ các tam giác đều $ADE,ABF$. Tam giác \(CEF\) là tam giác gì? Chọn câu trả lời đúng nhất
Câu 16 :
Cho tam giác \(ABC\) có \(BC = 6cm.\) Trên cạnh \(AB\) lấy các điểm \(D\) và \(E\) sao cho \(AD = BE.\) Qua \(D,E\) lần lượt vẽ các đường thẳng song song với \(BC,\) cắt \(AC\) theo thứ tự ở \(G\) và \(H\). Tính tổng \(DG + EH.\)
Lời giải và đáp án
Câu 1 :
Hãy chọn câu sai:
Đáp án : B Lời giải chi tiết :
Dấu hiệu nhận biết: + Tứ giác có các cạnh đối song song là hình bình hành nên A đúng. + Tứ giác có các cạnh đối bằng nhau là hình bình hành nên C đúng. + Tứ giác có các góc đối bằng nhau là hình bình hành nên D đúng. Nhận thấy hình thang có hai góc kề một đáy bằng nhau là hình thang cân nên B sai.
Câu 2 :
Hãy chọn câu đúng. Tứ giác $ABCD$ là hình bình hành nếu.
Đáp án : D Phương pháp giải :
Sử dụng dấu hiệu nhận biết hình bình hành. + Tứ giác có các cạnh đối song song là hình bình hành + Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành. + Tứ giác có các góc đối bằng nhau là hình bình hành Lời giải chi tiết :
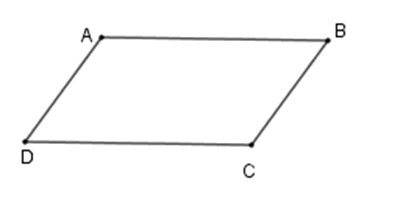 + Tứ giác \(ABCD\) là hình bình hành khi $AB$ //$CD$ ,$BC{\rm{//}}AD$ nên C sai. + Tứ giác \(ABCD\) là hình bình hành khi $\widehat A = \widehat C;\widehat B = \widehat D$ nên D đúng. + A, B sai vì chưa đủ điều kiện để kết luận. Chú ý
Một số em chọn C là sai vì ở dấu hiệu nhận biết : “Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.” Nghĩa là phải cùng một cặp cạnh đối vừa song song vừa bằng nhau thì tứ giác đó là hình bình hành.
Câu 3 :
Hãy chọn câu đúng. Cho hình bình hành $ABCD$ có các điều kiện như hình vẽ, trong hình có: 
Đáp án : A Phương pháp giải :
Sử dụng dấu hiệu nhận biết hình bình hành. Dấu hiệu nhận biết: + Tứ giác có các cạnh đối song song là hình bình hành + Tứ giác có các cạnh đối bằng nhau là hình bình hành. + Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành. + Tứ giác có các góc đối bằng nhau là hình bình hành. + Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành. Lời giải chi tiết :
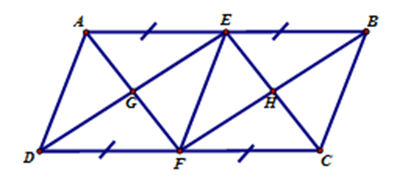 + Vì \(ABCD\) là hình bình hành nên \(AB{\rm{//}}CD\); \(AD{\rm{//}}BC\) . + Xét tứ giác \(AEFD\) có \(AE = FD;\,AE{\rm{//}}FD\) (do \(AB{\rm{//}}CD\)) nên \(AEFD\) là hình bình hành. + Xét tứ giác \(BEFC\) có \(BE = FC;\,BE{\rm{//}}FC\) (do \(AB{\rm{//}}CD\)) nên \(BEFC\) là hình bình hành. + Xét tứ giác \(AECF\) có \(AE = FC;\,AE{\rm{//}}FC\) (do \(AB{\rm{//}}CD\)) nên \(AECF\) là hình bình hành. + Xét tứ giác \(BEDF\) có \(BE = FD;\,BE{\rm{//}}FD\) (do \(AB{\rm{//}}CD\)) nên \(BEDF\) là hình bình hành. + Vì \(AECF\) là hình bình hành nên \(AF{\rm{//}}EC \Rightarrow EH{\rm{//}}GF\) ; vì \(BEDF\) là hình bình hành nên \(ED{\rm{//}}BF \Rightarrow EG{\rm{//}}HF\) Suy ra \(EGHF\) là hình bình hành. Vậy có tất cả \(6\) hình bình hành: \(ABCD\); \(AEFD\); \(BEFC\); \(AECF\); \(BEDF\); \(EGHF\). Chú ý
Một số em đếm thiếu hình bình hành \(ABCD\) hoặc \(EGHF\) dẫn đến chọn sai đáp án.
Câu 4 :
Cho hình bình hành $ABCD$ có \(\widehat A = 3\widehat B\) . Số đo các góc của hình bình hành là:
Đáp án : D Phương pháp giải :
Sử dụng tính chất hình bình hành và định lí tổng các góc trong một tứ giác Lời giải chi tiết :
Trong hình bình hành $ABCD$ có: \(\widehat A = \widehat C,\widehat B = \widehat D\) (tính chất), \(\widehat A = 3\widehat B\) Theo định lí tổng các góc trong tứ giác ta có: \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \Rightarrow 2\left( {\widehat A + \widehat B} \right) = 360^\circ \Rightarrow \widehat A + \widehat B = 180^\circ \) \( \Rightarrow 3\widehat B + \widehat B = 180^\circ \Rightarrow \widehat B = 45^\circ \) \( \Rightarrow \widehat A = 3\widehat B = 3.45^\circ = 135^\circ \) Vậy \(\widehat A = \widehat C = 135^\circ ;\widehat B = \widehat D = 45^\circ \).
Câu 5 :
Tính số đo các góc của hình bình hành $ABCD$ biết \(\widehat D - \widehat C = {30^0}\). Ta được:
Đáp án : B Phương pháp giải :
Sử dụng tính chất hình bình hành và định lí tổng các góc trong một tứ giác Lời giải chi tiết :
Trong hình bình hành $ABCD$ có: \(\widehat A = \widehat C,\widehat B = \widehat D\) (tính chất), \(\widehat D - \widehat C = {30^0} \Rightarrow \widehat D = \widehat C + 30^\circ \) nên \(\widehat B = \widehat D = \widehat C + 30^\circ \) Theo định lí tổng các góc trong tứ giác ta có: $\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \Rightarrow 2\left( {\widehat A + \widehat B} \right) = 360^\circ \Rightarrow \widehat A + \widehat B = 180^\circ $\( \Leftrightarrow \widehat C + \widehat C + 30^\circ = 180^\circ \Rightarrow 2\widehat C = 150^\circ \) \( \Leftrightarrow \widehat C = 75^\circ \) $ \Rightarrow \widehat D = \widehat C + 30^\circ = 75^\circ + 30^\circ = 105^\circ $ Do đó $\widehat A = \widehat C = {75^0}\,\& \,\,\widehat B = \widehat D = {105^0}$.
Câu 6 :
Hãy chọn câu trả lời sai. Cho hình vẽ, ta có: 
Đáp án : C Phương pháp giải :
Sử dụng dấu hiệu nhận biết và tính chất hình bình hành. Lời giải chi tiết :
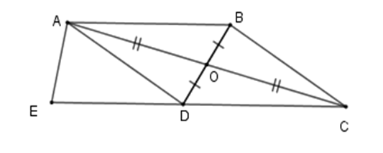 Từ hình vẽ ta có \(O\) là trung điểm của \(BD\) và \(AC\). Do đó tứ giác \(ABCD\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm mỗi đường, suy ra tứ giác \(ABCD\) là hình bình hành\( \Rightarrow \) A đúng. Vì \(ABCD\) là hình bình hành nên \(AB{\rm{//}}DC;\,AD{\rm{//}}BC\) (tính chất) \( \Rightarrow \) B, D đúng. Chưa đủ điều kiện để \(ABCE\) là hình thang cân.
Câu 7 :
Tỉ số độ dài hai cạnh của hình bình hành là \(3:5\). Còn chu vi của nó bằng \(48cm\). Độ dài hai cạnh kề của hình bình hành là:
Đáp án : D Phương pháp giải :
Gọi độ dài hai cạnh của hình bình hành là \(a\) và \(b\) rồi áp dụng tính chất dãy tỉ số bằng nhau để tìm \(a,b\). Lưu ý: Tổng của \(a,b\) là nửa chu vi hình bình hành. Lời giải chi tiết :
Gọi độ dài hai cạnh của hình bình hành là \(a\) và \(b\) với \(a,b > 0.\) Theo bài ra ta có: \(\dfrac{a}{3} = \dfrac{b}{5}\). Nửa chu vi của hình bình hành là: \(48:2 = 24cm\). Suy ra: \(a+b=24cm.\) Theo tính chất của dãy tỉ số bằng nhau ta có: \(\begin{array}{l}\dfrac{a}{3} = \dfrac{b}{5} = \dfrac{{a + b}}{{3 + 5}} = \dfrac{{24}}{8} = 3\\ \Rightarrow a = 3. 3 = 9\\b = 3. 5 = 15\end{array}\). Vậy hai cạnh của hình bình hành là \(9cm\) và \(15cm\).
Câu 8 :
Hai góc kề nhau của một hình bình hành không thể có số đo là:
Đáp án : B Phương pháp giải :
Dựa vào tính chất hình bình hành và định lí tổng các góc trong một tứ giác Lời giải chi tiết :
Trong hình bình hành có các góc đối bằng nhau và tổng các góc trong hình bình hành phải bằng \(360^\circ \) nên ta có: \(\begin{array}{l}60^\circ . 2 + 120^\circ . 2 = 360^\circ \\40^\circ . 2 + 50^\circ . 2 = 180^\circ \ne 360^\circ \\130^\circ . 2 + 50^\circ . 2 = 360^\circ \\105^\circ . 2 + 75^\circ . 2 = 360^\circ \end{array}\). Do đó hai góc kề của hình bình hành không thể có số đo \(40^\circ ; 50^\circ \). Cho tam giác $ABC$ và $H$ là trực tâm. Các đường thẳng vuông góc với $AB$ tại $B$ , vuông góc với $AC$ tại $C$ cắt nhau ở $ D$ . Câu 9
Chọn câu trả lời đúng nhất. Tứ giác $BDCH$ là hình gì?
Đáp án : B Phương pháp giải :
Bước 1: Sử dụng quan hệ từ vuông góc đến song song để chứng minh các cặp cạnh song song. Bước 2: Sử dụng dấu hiệu nhận biết của hình bình hành để suy ra $BDCH$ là hình bình hành Lời giải chi tiết :
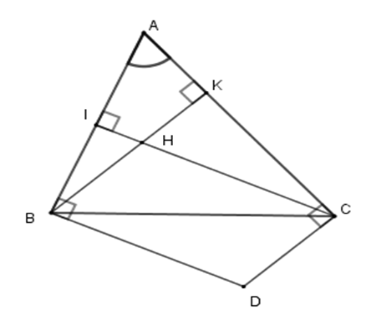 Gọi \(BK;\,CI\) là các đường cao của tam giác \(ABC\) . Khi đó \(BK \bot AC;\,CI \bot AB\) hay \(BH \bot AC;\,CH \bot AB\) (vì \(H\) là trực tâm). Lại có \(BD \bot AB;\,CD \bot AC\) (giả thiết) nên $BD{\rm{//}}CH$ (cùng vuông với \(AB\) ) và $CD{\rm{//}}BH$ (cùng vuông với \(AC\) ) Suy ra tứ giác \(BHCD\) là hình bình hành (dhnb). Câu 10
Tính số đo góc \(BDC\) , biết $\widehat {BAC} = 50^\circ $.
Đáp án : D Phương pháp giải :
Bước 1: Sử dụng định lý tổng các góc trong tứ giác để tính góc \(IHK\) . Bước 2: Sử dụng tính chất của hình bình hành để tính góc \(BDC\) . Lời giải chi tiết :
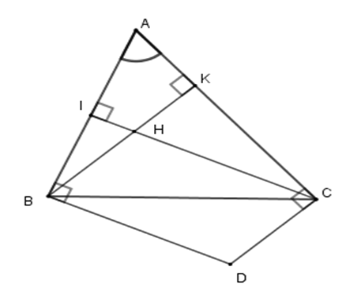 Xét tứ giác \(AIHK\) có \(\widehat A + \widehat {AIH} + \widehat {IHK} + \widehat {AKH} = 360^\circ \) (định lý tổng các góc trong tứ giác) \( \Rightarrow \widehat {AHK} = 360^\circ - 50^\circ - 90^\circ - 90^\circ = 130^\circ \) . Suy ra \(\widehat {BHC} = \widehat {IHK} = 130^\circ \) (hai góc đối đỉnh) Vì tứ giác \(BHCD\) là hình bình hành nên $\widehat {BDC} = \widehat {BHC} = 130^\circ $ (tính chất). Vậy \(\widehat {BDC} = 130^\circ \) .
Câu 11 :
Cho tứ giác $ABCD$ . Gọi$E$ , $F$ lần lượt là giao điểm của $AB$ và $CD$ , $AD$ và $BC;$ $M,N,P,Q$ lần lượt là trung điểm của $AE$ , $EC$ , $CF$ ,$FA$ . Khi đó \(MNPQ\) là hình gì? Chọn đáp án đúng nhất.
Đáp án : A Phương pháp giải :
Bước 1: Sử dụng tính chất đường trung bình của tam giác để chứng minh các cạnh song song và bằng nhau. Bước 2: Sử dụng dấu hiệu nhận biết để suy ra \(MNPQ\) là hình bình hành. Lời giải chi tiết :
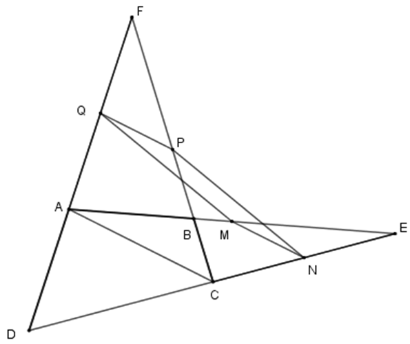 Nối \(AC\) .Vì $M,N$ lần lượt là trung điểm của$AE$ , $EC$ nên \(MN\) là đườn gtrung bình của tam giác \(EAC\) suy ra \(MN{\rm{//}}AC;\,MN = \dfrac{1}{2}AC\) $\left( 1 \right)$ . Tương tự \(PQ\) là đường trung bình của tam giác \(FAC\) suy ra \(PQ{\rm{//}}AC;\,PQ = \dfrac{1}{2}AC\) \(\left( 2 \right)\) . Từ \(\left( 1 \right);\,\left( 2 \right)\) suy ra \(PQ{\rm{//}}NM;\,PQ = MN\) nên \(MNPQ\) là hình bình hành (dhnb).
Câu 12 :
Hãy chọn câu sai.
Đáp án : C Lời giải chi tiết :
Trong hình bình hành: + Hình bình hành có các cạnh đối song song. + Các cạnh đối bằng nhau + Các góc đối bằng nhau + Hai đường chéo cắt nhau tại trung điểm của mỗi đường nên C sai.
Câu 13 :
Cho hình bình hành $ABCD$ . Gọi $I,{\rm{ }}K$ theo thứ tự là trung điểm của $CD,{\rm{ }}AB$ . Đường chéo $BD$ cắt $AI,{\rm{ }}CK$ theo thứ tự ở $E,{\rm{ }}F$ . Chọn khẳng định đúng.
Đáp án : B Phương pháp giải :
Bước 1: Chứng minh tứ giác $AKCI$ là hình bình hành để suy ra \(AI{\rm{//}}CK\) .Bước 2: Sau đó sử dụng định lí đường trung bình của các tam giác \(\Delta DCF,\Delta ABE\) để suy ra mối quan hệ giữa \(DE;\,EF;\,FB\) . Lời giải chi tiết :
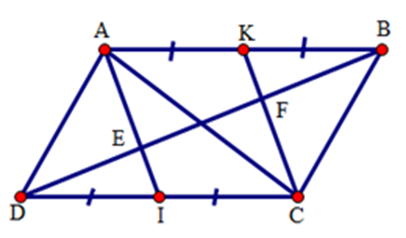 Vì \(AK = \dfrac{{AB}}{2},IC = \dfrac{{CD}}{2}\) (gt) mà \(AB = CD\) (cạnh đối hình bình hành) nên \(AK = IC\) . Vì $AB{\rm{//}}CD(gt),K \in AB,I \in DC \Rightarrow AK{\rm{//}}IC$ . Tứ giác $AKCI$ có \(AK{\rm{//}}CI,AK = IC(cmt)\) nên là hình bình hành. Suy ra \(AI{\rm{//}}CK\) . Mà \(E \in AI,F \in CK \Rightarrow EI{\rm{//}}CF,KF{\rm{//}}AE\) . Xét \(\Delta DCF\) có: \(DI = IC(gt),IE{\rm{//}}CF(cmt) \Rightarrow ED = FE\,\,\,(1)\) Xét \(\Delta ABE\) có: \(AK = KB(gt),KF{\rm{//}}AE(cmt) \Rightarrow EF = FB\,\,\,\,(2)\). Từ (1) và (2) suy ra \(ED = FE = FB\).
Câu 14 :
Cho hình bình hành $ABCD$ . Trên đường chéo $BD$ lấy hai điểm $E$ và $F$ sao cho \(BE = DF < \dfrac{1}{2}BD\) . Chọn khẳng định đúng.
Đáp án : A Phương pháp giải :
Chứng minh tứ giác $AECF$ là hình bình hành để suy ra mối quan hệ giữa \(FA\) và \(CE\) . Lời giải chi tiết :
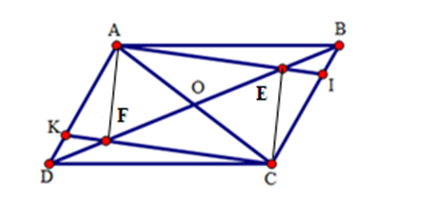 Gọi $O$ là giao điểm của $AC$ và $BD$. Ta có \(OA = OC,OB = OD\) . Mà \(BE = DF(gt) \Rightarrow OE = FO\) . Tứ giác $AECF$ có hai đường chéo $AC$ và $EF$ cắt nhau tại trung điểm \(O\) nên $AECF$ là hình bình hành $ \Rightarrow FA = CE$
Câu 15 :
Cho hình bình hành $ABCD$ có \(\widehat A = \alpha > 90^\circ \) . Ở phía ngoài hình bình hành vẽ các tam giác đều $ADE,ABF$. Tam giác \(CEF\) là tam giác gì? Chọn câu trả lời đúng nhất
Đáp án : C Phương pháp giải :
Chứng minh các tam giác bằng nhau để có các cạnh bằng nhau từ đó suy ra tam giác \(CEF\) là tam đều. Lời giải chi tiết :
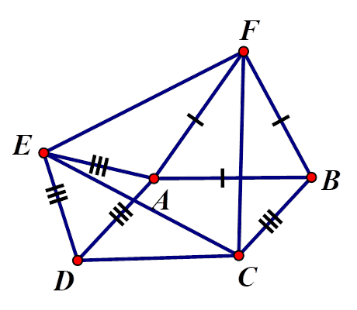 Ta có: \(\widehat {EAF} = 360^\circ - \widehat {BAF} - \widehat {EAD} - \alpha \) \( = 360^\circ - 60^\circ - 60^\circ - \alpha = 240^\circ - \alpha \) Ta có:\(\widehat {ADC} = 180^\circ - \alpha \) ; \(\widehat {CDE} = \widehat {ADC} + \widehat {EDA} = 180^\circ - \alpha + 60^\circ = 240^\circ - \alpha \)\( \Rightarrow \widehat {CDE} = \widehat {FAE}\) Xét \(\Delta CDE\) và \(\Delta FAE\) có: \(\left\{ \begin{array}{l}CD = FA(gt)\\\widehat {CDF} = \widehat {EAF}(cmt)\\DE = EA(gt)\end{array} \right.\)\( \Rightarrow \Delta CDE = \Delta FAE\left( {c.g.c} \right) \Rightarrow CE = FE\,\,(1)\) Tương tự , ta có: \(\widehat {ABC} = 180^\circ - \alpha \) ; \(\widehat {CBF} = \widehat {ABC} + \widehat {FBA} = 180^\circ - \alpha + 60^\circ = 240^\circ - \alpha \Rightarrow \widehat {CBF} = \widehat {FAE}\) Xét \(\Delta FBC\) và \(\Delta FAE\) có: \(\left\{ \begin{array}{l}FB = FA(gt)\\\widehat {CBF} = \widehat {EAF}(cmt)\\CB = EA(gt)\end{array} \right.\)\( \Rightarrow \Delta FBC = \Delta FAE\left( {c.g.c} \right) \Rightarrow CF = FE\,\,(2)\) Từ (1) và (2) suy ra \(CF = FE = EC\) nên tam giác $CEF$ đều.
Câu 16 :
Cho tam giác \(ABC\) có \(BC = 6cm.\) Trên cạnh \(AB\) lấy các điểm \(D\) và \(E\) sao cho \(AD = BE.\) Qua \(D,E\) lần lượt vẽ các đường thẳng song song với \(BC,\) cắt \(AC\) theo thứ tự ở \(G\) và \(H\). Tính tổng \(DG + EH.\)
Đáp án : C Phương pháp giải :
+ Kẻ \(HM//AB\,\,\left( {M \in BC} \right)\). + Chứng minh \(DG = MC\) từ hai tam giác bằng nhau từ đó tính tổng \(DG + EH\). Lời giải chi tiết :
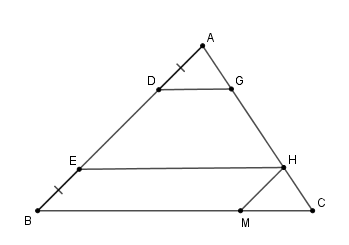 Kẻ \(HM//AB\,\,\left( {M \in BC} \right)\). Xét tứ giác \(EHMB\) có \(MH//EB;EH//BM\) nên \(EHMB\) là hình bình hành. Suy ra \(EH = BM;\,EB = HM\) (tính chất hình bình hành) mà \(AD = BE \Rightarrow AD = MH\). Lại có: \(DG//BC \Rightarrow \widehat {ADG} = \widehat {ABC}\) (hai góc ở vị trí đồng vị) (1) Và \(HM//AB \Rightarrow \widehat {HMC} = \widehat {ABC}\) và \(\widehat {CHM} = \widehat {CAB}\) (hai góc ở vị trí đồng vị) (2) Từ (1) và (2) suy ra: \(\widehat {HMC} = \widehat {ADG}\left( { = \widehat {ABC}} \right)\). Xét \(\Delta ADG\) và \(\Delta HMC\) có: \(\left\{ \begin{array}{l}\widehat {MHC} = \widehat {DAG}\left( {cmt} \right)\\AD = HM\,\left( {cmt} \right)\\\widehat {HMC} = \widehat {ADG}\left( {cmt} \right)\end{array} \right.\) nên \(\Delta ADG = \Delta HMC\left( {g - c - g} \right) \Rightarrow DG = MC\). Ta có: \(DG + EH = MC + BM = BC = 6cm\).
|












