Trắc nghiệm Bài 6: Đối xứng trục Toán 8Đề bài
Câu 1 :
Hãy chọn câu đúng. Trục đối xứng của hình thang cân là:
Câu 2 :
Hãy chọn câu đúng?
Câu 3 :
Cho tam giác $ABC$ cân tại $B$ , các đường trung tuyến $AA',BB',CC'$ . Trục đối xứng của tam giác $ABC$ là:
Câu 4 :
Hãy chọn câu sai:
Câu 5 :
Cho hình vẽ. Hãy chọn câu đúng.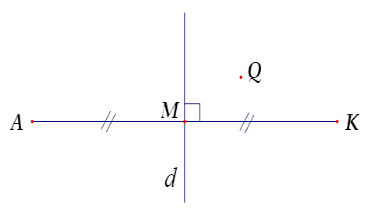 
Câu 6 :
Hãy chọn câu sai.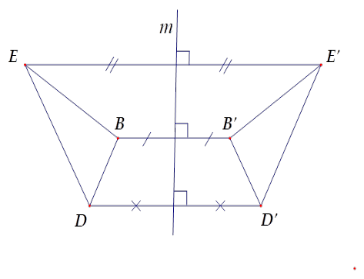 
Câu 7 :
Cho đoạn thẳng $AB$ có độ dài $3cm$và đường thẳng $d$ . Đoạn thẳng $A'B'$ đối xứng với $AB$ qua $d$ . Độ dài đoạn thẳng $A'B'$ là:
Câu 8 :
Cho tam giác $ABC$ và tam giác $A'B'C'$ đối xứng nhau qua đường thẳng $d$ biết $AB = 4cm,BC = 7cm$ và chu vi của tam giác $ABC = 17cm$. Khi đó độ dài cạnh $C'A'$ của tam giác $A'B'C'$ là:
Câu 9 :
Cho tam giác \(ABC\), trong đó \(AB = 11\,cm,AC = 15\,cm\). Vẽ hình đối xứng với tam giác \(ABC\) qua trục là cạnh \(BC\). Chu vi của tứ giác tạo thành là:
Cho hình vuông $ABCD$ cạnh bằng $a$. $M$ và $N$ là hai điểm lưu động lần lượt trên cạnh $AB$ và $AD$ sao cho \(\widehat {MCN} = {45^0}\). Vẽ tia $Cx$ vuông góc với $CN,Cx$ cắt đường thẳng $AB$ tại $E$. Câu 10
Chọn kết luận đúng nhất.
Câu 11
Tính chu vi của tam giác \(AMN\) theo \(a\) .
Cho tam giác \(ABC\) có \(\widehat A = {20^0};\widehat B = {80^0}\), \(d\) là trung trực của cạnh \(AB\). Trên cạnh \(AC\), lấy điểm \(M\) sao cho \(AM = BC\) và gọi \(M'\) là điểm đối xứng của \(M\) qua \(d\). Câu 12
Tam giác \(M'BC\) là tam giác gì? Chọn đáp án đúng nhất.
Câu 13
Tính góc \(BMC\).
Câu 14 :
Cho hai điểm $A,B$ nằm trên cùng một nửa mặt phẳng bờ là đường thẳng $d$ . Gọi $B'$ là điểm đối xứng của $B$ qua đường thẳng $d$. Tìm trên đường thẳng $d$ điểm $M$ sao cho tổng $MA + MB$ nhỏ nhất. Chọn khẳng định đúng nhất.
Câu 15 :
Trên tia phân giác góc ngoài tại đỉnh \(C\) của tam giác \(ABC,\) lấy điểm \(M\) (\(M\) khác \(C\)). Chọn câu đúng.
Lời giải và đáp án
Câu 1 :
Hãy chọn câu đúng. Trục đối xứng của hình thang cân là:
Đáp án : D Lời giải chi tiết :
Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
Câu 2 :
Hãy chọn câu đúng?
Đáp án : A Lời giải chi tiết :
+ Hình thang cân có trục đối xứng là đường thẳng đi qua trung điểm hai đáy nên hình thang cân có một trục đối xứng. Do đó A sai. + Tam giác cân có một trục đối xứng là đường trung trực hạ từ đỉnh cân nên B sai. + Tam giác thường thì không có trục đối xứng nên C sai. + Tam giác đều có ba trục đối xứng là ba đường trung trực của tam giác nên D đúng.
Câu 3 :
Cho tam giác $ABC$ cân tại $B$ , các đường trung tuyến $AA',BB',CC'$ . Trục đối xứng của tam giác $ABC$ là:
Đáp án : B Phương pháp giải :
Áp dụng định nghĩa hai điểm đối xứng nhau qua trục: hai điểm $A,A'$ được gọi là đối xứng nhau qua $d$ nếu $d$ là đường trung trực của $AA'$ . Lời giải chi tiết :
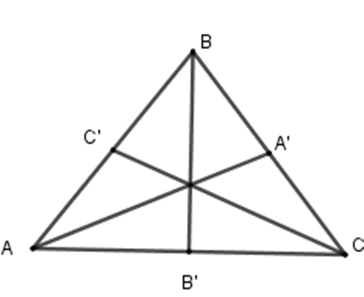 Do tam giác $ABC$ cân tại $B$ , nên đường trung tuyến $BB'$ đồng thời là đường trung trực. Do đó $BB'$ là trục đối xứng của tam giác $ABC$.
Câu 4 :
Hãy chọn câu sai:
Đáp án : D Phương pháp giải :
Ta sử dụng chú ý: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau. Lời giải chi tiết :
Vì hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau nên D sai. Chú ý
Một số em chọn C là sai vì nếu hai tam giác đối xứng với nhau qua một đường thẳng thì chúng bằng nhau nên chu vi của chúng bằng nhau.
Câu 5 :
Cho hình vẽ. Hãy chọn câu đúng.
Đáp án : C Phương pháp giải :
Ta sử dụng định nghĩa: Hai điểm $A,B$ gọi là đối xứng với nhau qua đường thẳng $d$ nếu $d$ là đường trung trực của đoạn thẳng nối hai điểm đó. Lời giải chi tiết :
Từ hình vẽ ta có đường thẳng \(d\) là đường trung trực của đoạn thẳng \(AK\) nên Điểm đối xứng với \(A\) qua đường thẳng \(d\) là \(K\).
Câu 6 :
Hãy chọn câu sai.
Đáp án : D Phương pháp giải :
Bước 1: Ta sử dụng định nghĩa: “ Hai điểm $A,B$ gọi là đối xứng với nhau qua đường thẳng $d$ nếu $d$ là đường trung trực của đoạn thẳng nối hai điểm đó ” để tìm các cặp điểm đối xứng nhau qua đường thẳng \(m\) . Bước 2: Từ đó suy ra các đoạn thẳng và tam giác đối xứng nhau qua đường thẳng \(m\) . Lời giải chi tiết :
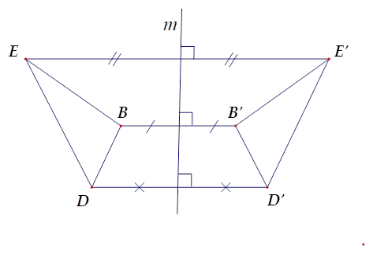 Từ hình vẽ ta có \(A\) và \(A'\) đối xứng nhau qua đường thẳng \(m\); \(B\) và \(B'\) đối xứng nhau qua đường thẳng \(m\); \(C\) và \(C'\) đối xứng nhau qua đường thẳng \(m\). Suy ra hai đoạn thẳng \(EB\) và \(E'B'\) đối xứng nhau qua \(m\). Hai đoạn thẳng \(DB\) và \(D'B'\) đối xứng nhau qua \(m\). Hai tam giác \(DEB\) và \(D'E'B'\) đối xứng nhau qua \(m\). Hai đoạn thẳng \(DE\) và \(D'E'\) đối xứng nhau qua \(m\) nên D sai. Chú ý
Các em có thể suy trực tiếp ra các đoạn thẳng đối xứng, các tam giác đối xứng mà không cần thông qua điểm.
Câu 7 :
Cho đoạn thẳng $AB$ có độ dài $3cm$và đường thẳng $d$ . Đoạn thẳng $A'B'$ đối xứng với $AB$ qua $d$ . Độ dài đoạn thẳng $A'B'$ là:
Đáp án : A Phương pháp giải :
Ta sử dụng chú ý: “ Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.” Từ đó suy ra độ dài đoạn $A'B'$. Lời giải chi tiết :
Vì đoạn thẳng $A'B'$ đối xứng với $AB$ qua $d$ nên \(A'B' = AB = 3\,cm\) .
Câu 8 :
Cho tam giác $ABC$ và tam giác $A'B'C'$ đối xứng nhau qua đường thẳng $d$ biết $AB = 4cm,BC = 7cm$ và chu vi của tam giác $ABC = 17cm$. Khi đó độ dài cạnh $C'A'$ của tam giác $A'B'C'$ là:
Đáp án : B Phương pháp giải :
Bước 1: Tính độ dài cạnh \(AC\) dựa vào chu vi tam giác \(ABC\) . Bước 2: Ta sử dụng chú ý: “ Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.” Từ đó suy ra độ dài đoạn $A'C'$. Lời giải chi tiết :
+ Xét tam giác \(ABC\) có chu vi \({P_{ABC}} = AB + AC + BC \Rightarrow AC = {P_{ABC}} - AB - BC = 17 - 4 - 7\) \( = 6\,cm\) . + Vì tam giác $ABC$ và tam giác $A'B'C'$ đối xứng nhau qua đường thẳng $d$ nên \(AC = A'C' = 6\,cm\) .
Câu 9 :
Cho tam giác \(ABC\), trong đó \(AB = 11\,cm,AC = 15\,cm\). Vẽ hình đối xứng với tam giác \(ABC\) qua trục là cạnh \(BC\). Chu vi của tứ giác tạo thành là:
Đáp án : A Phương pháp giải :
Bước 1: Ta sử dụng chú ý: “ Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.” Bước 2: Từ đó suy ra độ dài các cạnh còn lại rồi tính chu vi tứ giác. Lời giải chi tiết :
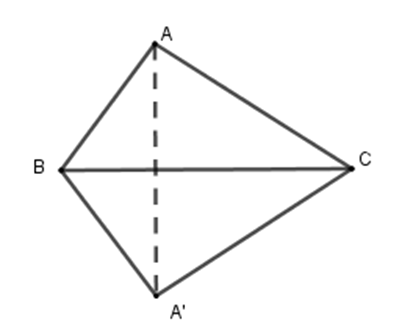 Gọi \(A'\) là điểm đối xứng với \(A\) qua \(BC\) . Khi đó tam giác \(A'BC\) đối xứng với tam giác \(ABC\) qua \(BC\) . Tứ giác tạo thành là \(ABCA'\) . Ta có \(A'B = AB = 11\,cm\) (vì \(A'B\) và \(AB\) đối xứng nhau qua \(BC\) ) \(A'C = AC = 15\,cm\) ( vì \(A'C\) và \(AC\) đối xứng nhau qua \(BC\) ) Chu vi tứ giác \(ABCA'\) là \(P = AB + AC + A'B + A'C = 11 + 15 + 11 + 15 = 52\,cm\) . Cho hình vuông $ABCD$ cạnh bằng $a$. $M$ và $N$ là hai điểm lưu động lần lượt trên cạnh $AB$ và $AD$ sao cho \(\widehat {MCN} = {45^0}\). Vẽ tia $Cx$ vuông góc với $CN,Cx$ cắt đường thẳng $AB$ tại $E$. Câu 10
Chọn kết luận đúng nhất.
Đáp án : C Phương pháp giải :
+ Ta chứng minh \(CE = CN\) suy ra tam giác \(CEN\) cân tại \(C\) . +Ta chứng minh $CM$ là tia phân giác đồng thời là trung trực của $NE$ nên $E$ đối xứng với $N$ qua $CM$. Lời giải chi tiết :
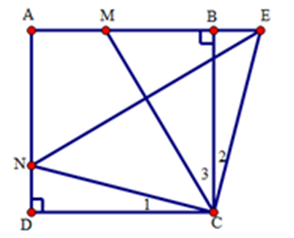 Ta có $CN \bot CE\,\left( {gt} \right)$ mà \(\widehat {MCN} = {45^0}\) nên \(\widehat {MCE} = {45^0}\) hay $\widehat {{C_2}} + \widehat {{C_3}} = {45^0}$. Mà $\widehat {{C_1}} + \widehat {{C_3}} = {45^0}$(vì \(\widehat {MCN} = {45^0}\)) nên $\widehat {{C_1}} = \widehat {{C_2}}$. Xét tam giác $CDN$ và tam giác $CBE$ có: $BC = DC$ (do $ABCD$ là hình vuông); \(\widehat D = \widehat B = {90^0}\) ; $\widehat {{C_1}} = \widehat {{C_2}}$(cmt) Suy ra \(\Delta CDN = \Delta CBE(g.c.g)\) .Suy ra $CN = CE$ Xét tam giác $CEN$ có $CN = CE$ (cmt) nên tam giác $CEN$ là tam giác cân tại $C$. Suy ra phân giác $CM$ đồng thời là đường trung trực của $NE$ . Vậy E là điểm đối xứng của $N$ qua $CM$ . Câu 11
Tính chu vi của tam giác \(AMN\) theo \(a\) .
Đáp án : D Phương pháp giải :
Bước 1: Ta sử dụng chú ý: “ Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.” Bước 2: Từ đó ta biến đổi các cạnh của tam giác để xuất hiện các cạnh của hình vuông để tính chu vi tam giác \(AMN\) . Lời giải chi tiết :
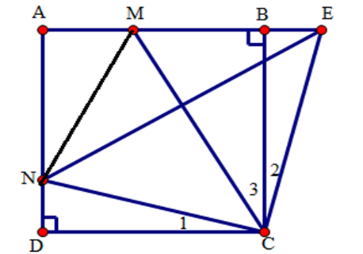 Ta có: \(\Delta CMN = \Delta CME\)(do tính đối xứng qua $CM$ ) Nên $MN = ME$ Suy ra chu vi tam giác \(AMN\) là: $AM + AN + MN = AM + AN{\rm{ }} + ME = AM + AN + MB + BE$ $ = AM + AN + MB + ND$ (vì \(\Delta CDN = \Delta CBE\) (cmt) nên $BE = ND$) $ = \left( {AM{\rm{ }} + MB} \right) + \left( {AN + ND} \right) = 2a$ Vậy chu vi tam giác $AMN$ bằng $2a$ . Cho tam giác \(ABC\) có \(\widehat A = {20^0};\widehat B = {80^0}\), \(d\) là trung trực của cạnh \(AB\). Trên cạnh \(AC\), lấy điểm \(M\) sao cho \(AM = BC\) và gọi \(M'\) là điểm đối xứng của \(M\) qua \(d\). Câu 12
Tam giác \(M'BC\) là tam giác gì? Chọn đáp án đúng nhất.
Đáp án : A Phương pháp giải :
Sử dụng tính chất đối xứng của điểm, đoạn thẳng qua đường thẳng. Chứng minh tam giác cân có một góc bằng \(60^\circ \). Lời giải chi tiết :
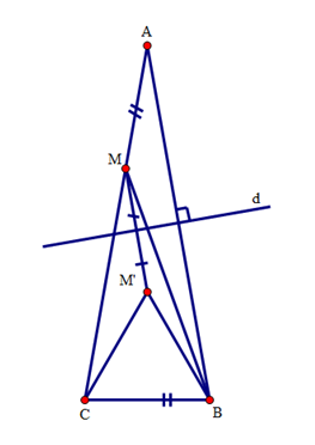 Do tính chất đối xứng qua \(d\), ta có \(AM = BM'\). Mà \(AM = BC\left( {gt} \right)\) nên \(BM' = BC\). Ta lại có: \(\widehat {M'BA} = \widehat {MAB} = {20^0}\) (do \(M,{\rm{ }}A\) đối xứng với \(M',{\rm{ }}B\) qua \(d\)). Suy ra \(\widehat {M'BC} = \widehat B - {20^0} = {80^0} - {20^0} = {60^0}\). Xét tam giác \(M'BC\) có \(BM' = BC\), \(\widehat {M'BC} = {60^0}\) do đó tam giác \(M'BC\) là tam giác đều. Câu 13
Tính góc \(BMC\).
Đáp án : B Phương pháp giải :
Ta thấy \(\widehat {BMC} = \widehat {CMM'} + \widehat {M'MB}\). Do đó để tính góc \(BMC\) ta lần lượt đi tính góc \(\widehat {CMM'}\) và \(\widehat {M'MB}\). Lời giải chi tiết :
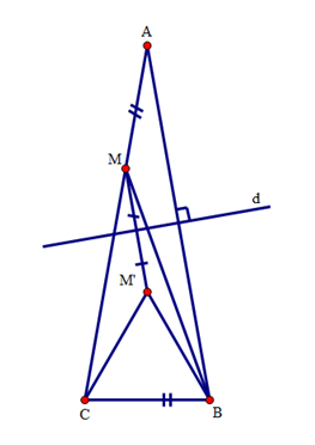 Ta cũng có: \(\widehat {MCB} = {180^0} - \left( {\widehat A + \widehat B} \right) = {180^0} - \left( {{{20}^0} + {{80}^0}} \right) = {80^0}\) Suy ra \(\widehat {MCM'} = \widehat {MCB} - \widehat {M'CB} = {80^0} - {60^0} = {20^0}\) Mà \(\widehat {CMM'} = \widehat A = {20^0}\)(góc đồng vị). Nên \(\widehat {MCM'} = \widehat {CMM'} = {20^ \circ }\) Suy ra \(M'C = M'M = M'B\). Ta lại có: \(\widehat {M'MB} = \widehat {M'BM}\) (tam giác \(M'MB\) cân tại đỉnh \(M'\)); \(\widehat {M'MB} = \widehat {MBA}\)(so le trong). Nên \(\widehat {M'BM} = \widehat {MBA} = \dfrac{1}{2}\widehat {M'BA} = {10^0}\) Vậy \(\widehat {BMC} = \widehat {CMM'} + \widehat {M'MB} = {20^0} + {10^0} = {30^0}\)
Câu 14 :
Cho hai điểm $A,B$ nằm trên cùng một nửa mặt phẳng bờ là đường thẳng $d$ . Gọi $B'$ là điểm đối xứng của $B$ qua đường thẳng $d$. Tìm trên đường thẳng $d$ điểm $M$ sao cho tổng $MA + MB$ nhỏ nhất. Chọn khẳng định đúng nhất.
Đáp án : B Phương pháp giải :
Ta nhân thấy nếu $A,{\rm{ }}B$ nằm trên hai nửa mặt phẳng đối nhau bờ là đường thẳng $d$ thì tổng $MA + MB$ nhỏ nhất là đoạn $AB$ . Do vậy ta tìm cách đưa bài toán về trường hợp này. Bằng cách dựng $B'$ đối xứng với $B$ qua $d$ ta đưa bài toán đã cho về trường hợp nêu trên vì $MB = MB'$ . Lời giải chi tiết :
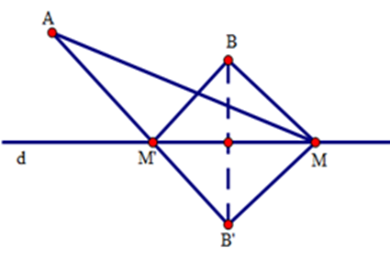 Gọi $B'$ là điểm đối xứng của $B$ qua đường thẳng $d$. $B'$ cố định. Ta có $MB = MB'$ (tính chất đối xứng trục). Xét ba điểm $M,{\rm{ }}A,{\rm{ }}B'$ ta có $MA + MB' \ge AB'$ Do đó $MA + MB \ge AB'$ Dấu “=” xảy ra khi và chỉ khi $A,M,B'$ thẳng hàng theo thứ tự đó hay $M$ là giao điểm của đoạn $AB'$ và đường thẳng $d$ . Vậy khi \(M \equiv M'\) là giao điểm của đoạn thẳng $AB'$ và đường thẳng $d$ thì tổng $MA + MB$ nhỏ nhất, trong đó $B'$ là điểm đối xứng của $B$ qua $d$ .
Câu 15 :
Trên tia phân giác góc ngoài tại đỉnh \(C\) của tam giác \(ABC,\) lấy điểm \(M\) (\(M\) khác \(C\)). Chọn câu đúng.
Đáp án : B Phương pháp giải :
+ Sử dụng tính chất đường trung trực của đoạn thẳng. + Sử dụng bất đẳng thức về ba cạnh của tam giác: Cho tam giác \(ABC\) thì \(\left| {AB - AC} \right| < BC < AB + AC\). Lời giải chi tiết :
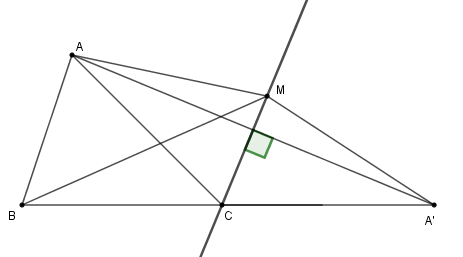 Trên tia đối của tia \(CB\) lấy điểm \(A'\) sao cho \(CA = CA'\) Khi đó ta có: \(\Delta CAA'\) cân tại \(C\) có \(CM\) là phân giác \(\widehat {ACA'}\) nên \(CM\) cũng là đường trung trực của \(AA'\). Từ đó ta có: \(MA = MA'\) Nên \(MA + MB = MA' + MB\). Xét tam giác \(MA'B\) có \(MA' + MB > A'B \Leftrightarrow MA + MB > A'C + BC\) Hay \(MA + MB > AC + BC\) (vì \(CA = CA'\)).
|
