Trắc nghiệm Bài tập ôn tập chương 2 Toán 8Đề bài
Câu 1 :
Phân thức 5x−73x2+6x xác định khi:
Câu 2 :
Đa thức thích hợp để điền vào chỗ trống trong đẳng thức x3−8......=x2+2x+43x là:
Câu 3 :
Đa thức P trong đẳng thức 5(y−x)25x2−5xy=x−yP là:
Câu 4 :
Kết quả của phép tính 3x−12xy−5x−22xy là:
Câu 5 :
Thực hiện phép tính sau: x3x2+1+xx2+1
Câu 6 :
Thực hiện phép tính sau 2x+55x2y2+85xy2+2x−1x2y2, ta được kết quả là:
Câu 7 :
Điền vào chỗ trống: 2x−6x+3−....=x+12.
Câu 8 :
Kết quả của phép tính 1x+1x(x+1)+...+1(x+9)(x+10) là:
Câu 9 :
Rút gọn biểu thức 1x+2+1(x+1)(x+2)+1(x+1)(2x+1) ta được
Câu 10 :
Chọn câu đúng.
Câu 11 :
Tìm P biết: P+4x−12x3−3x2−4x+12=3x−3−x24−x2
Câu 12 :
Thực hiện phép tính 3x+15x2−4:x+5x−2 ta được:
Câu 13 :
Rút gọn biểu thức x4+4x2+55x3+5⋅2xx2+4⋅3x3+3x4+4x2+5 ta được:
Câu 14 :
Biểu thức P=x−12−x:x−1x+2⋅x−24−x2 có kết quả rút gọn là:
Câu 15 :
Tìm biểu thức Q, biết: 5xx2+2x+1⋅Q=xx2−1
Câu 16 :
Tìm x, biết: 1x⋅xx+1⋅x+1x+2⋅x+2x+3⋅x+3x+4⋅x+4x+5⋅x+5x+6=1
Câu 17 :
Thực hiện phép tính x−6x2+1⋅3x2−3x+3x2−36+x−6x2+1⋅3xx2−36 ta được kết quả là
Câu 18 :
Tìm biểu thức M, biết x+2yx3−8y3⋅M=5x2+10xyx2+2xy+4y2
Câu 19 :
Thực hiện phép tính sau (2x3x+1−1):(1−8x29x2−1), ta được kết quả là:
Câu 20 :
Thực hiện phép tính C=2x2+4x+8x3−3x2−x+3:x3−8(x+1)(x−3)
Câu 21 :
Cho Q=(x2+3xx3+3x2+9x+27+3x2+9):(1x−3−6xx3−3x2+9x−27). Rút gọn Q ta được.
Cho biểu thức P=10xx2+3x−4−2x−3x+4+x+11−x Câu 22
Rút gọn P ta được
Câu 23
Tính giá trị của P khi x=−1.
Câu 24
Tìm x∈Z để P+1∈Z.
Câu 25 :
Cho x;y;z≠0 thỏa mãn x+y+z=0. Chọn câu đúng về biểu thức A=xyx2+y2−z2+yzy2+z2−x2+zxz2+x2−y2.
Câu 26 :
Giá trị lớn nhất của phân thức 5x2−6x+10 là :
Lời giải và đáp án
Câu 1 :
Phân thức 5x−73x2+6x xác định khi:
Đáp án : C Phương pháp giải :
ĐKXĐ của phân thức: Mẫu thức khác 0. Lời giải chi tiết :
ĐK: 3x2+6x≠0⇔3x(x+2)≠0⇔{x≠0x≠−2
Câu 2 :
Đa thức thích hợp để điền vào chỗ trống trong đẳng thức x3−8......=x2+2x+43x là:
Đáp án : A Phương pháp giải :
Biến đổi phân thức x2+2x+43x sao cho có tử thức là x3−8. Từ đó suy ra đa thức cần điền vào chỗ trống Lời giải chi tiết :
x2+2x+43x=(x−2)(x2+2x+4)3x(x−2)=x3−83x(x−2)⇒x3−83x(x−2)=x3−8...... Vậy đa thức cần tìm là 3x(x−2) Chú ý
Các em có thể dùng tính chất hai phân thức bằng nhau AB=CD(A;D≠0)⇔A.D=B.C để tìm ra đa thức cần điền.
Câu 3 :
Đa thức P trong đẳng thức 5(y−x)25x2−5xy=x−yP là:
Đáp án : D Phương pháp giải :
Biến đổi phân thức vế trái sao cho có tử thức bằng với tử thức bên vế phải Từ đó tìm ra đa thức P. Lời giải chi tiết :
Ta có: 5(y−x)25x2−5xy=5(x−y)25x(x−y)=x−yx⇒x−yx=x−yP⇒P=x.
Câu 4 :
Kết quả của phép tính 3x−12xy−5x−22xy là:
Đáp án : C Phương pháp giải :
Sử dụng kiến thức trừ 2 phân thức cùng mẫu :AM−BM=A−BM Lời giải chi tiết :
3x−12xy−5x−22xy=3x−1−5x+22xy=−2x+12xy. Chú ý
Các em chú ý dấu khi cộng trừ các hạng tử.
Câu 5 :
Thực hiện phép tính sau: x3x2+1+xx2+1
Đáp án : D Phương pháp giải :
Sử dụng kiến thức cộng 2 phân thức cùng mẫu, phân tích đa thức thành nhân tử và rút gọn. Lời giải chi tiết :
Ta có x3x2+1+xx2+1=x3+xx2+1=x(x2+1)x2+1=x.
Câu 6 :
Thực hiện phép tính sau 2x+55x2y2+85xy2+2x−1x2y2, ta được kết quả là:
Đáp án : D Phương pháp giải :
Qui đồng mẫu thức rồi cộng các phân thức Rút gọn phân thức thu được Lời giải chi tiết :
2x+55x2y2+85xy2+2x−1x2y2=2x+5+8x+10x−55x2y2=20x5x2y2=4xy2.
Câu 7 :
Điền vào chỗ trống: 2x−6x+3−....=x+12.
Đáp án : C Phương pháp giải :
Gọi phân thức cần điền là P. Ta sử dụng A−P=B suy ra P=A−B. Từ đó thực hiện phép qui đồng và cộng, trừ các phân thức để tìm P. Lời giải chi tiết :
Gọi phân thức cần điền là P, khi đó P=2x−6x+3−x+12=2(2x−6)−(x+3)(x+1)2(x+3)=4x−12−x2−x−3x−32(x+3)=−x2−152(x+3).
Câu 8 :
Kết quả của phép tính 1x+1x(x+1)+...+1(x+9)(x+10) là:
Đáp án : A Phương pháp giải :
Sử dụng kiến thức 1x(x+1)=1x−1x+1; cộng 2 phân thức khác mẫu. Lời giải chi tiết :
Ta có : 1x+1x(x+1)+...+1(x+9)(x+10) =1x+1x−1x+1+1x+1−1x+2...+1x+9−1x+10=1x+1x+0+...+0−1x+10=2x−1x+10=2x+20−xx(x+10)=x+20x(x+10).
Câu 9 :
Rút gọn biểu thức 1x+2+1(x+1)(x+2)+1(x+1)(2x+1) ta được
Đáp án : C Phương pháp giải :
Sử dụng kiến thức quy đồng mẫu nhiều phân thức; cộng các phân thức cùng mẫu, phân tích đa thức thành nhân tử và rút gọn. Lời giải chi tiết :
Điều kiện: x≠−1;x≠−2;x≠−12. 1x+2+1(x+1)(x+2)+1(x+1)(2x+1)=(2x+1)(x+1)+2x+1+x+2(x+1)(x+2)(2x+1)=2x2+x+2x+1+2x+1+x+2(x+1)(x+2)(2x+1)=2x2+6x+4(x+1)(x+2)(2x+1)=2(x2+3x+2)(x+1)(x+2)(2x+1)=2(x2+x+2x+2)(x+1)(x+2)(2x+1)=2[x(x+1)+2(x+1)](x+1)(x+2)(2x+1)=2(x+1)(x+2)(x+1)(x+2)(2x+1)=22x+1.
Câu 10 :
Chọn câu đúng.
Đáp án : A Phương pháp giải :
Sử dụng kiến thức quy đồng mẫu nhiều phân thức; cộng, trừ các phân thức cùng mẫu và rút gọn. Chú ý rằng: x3−1=(x−1)(x2+x+1) để tìm mẫu thức chung. Lời giải chi tiết :
Điều kiện: x≠1. 4x2−3x+5x3−1−1−2xx2+x+1−6x−1=4x2−3x+5−(1−2x)(x−1)−6(x2+x+1)(x−1)(x2+x+1)=4x2−3x+5−x+1+2x2−2x−6x2−6x−6(x−1)(x2+x+1)=−12xx3−1.
Câu 11 :
Tìm P biết: P+4x−12x3−3x2−4x+12=3x−3−x24−x2
Đáp án : B Phương pháp giải :
Sử dụng quy tắc chuyển vế, quy tắc đổi dấu, trừ các phân thức khác mẫu, phân tích đa thức thành nhân tử và rút gọn. Lời giải chi tiết :
ĐK: x≠{−2;2;3}. P+4x−12x3−3x2−4x+12=3x−3−x24−x2P=3x−3−x24−x2−4x−12x3−3x2−4x+12P=3x−3+x2(x−2)(x+2)−4x−12x2(x−3)−4(x−3)P=3(x2−4)(x−3)(x2−4)+x2(x−3)(x−3)(x2−4)−4x−12(x−3)(x2−4) P=3x2−12+x3−3x2−4x+12(x−3)(x2−4) P=x3−4x(x−3)(x−2)(x+2)P=x(x2−4)(x−3)(x−2)(x+2)=xx−3
Câu 12 :
Thực hiện phép tính 3x+15x2−4:x+5x−2 ta được:
Đáp án : D Phương pháp giải :
Áp dụng quy tắc chia hai phân thức đại số: AB:CD=AB.DC=A.DB.C Lời giải chi tiết :
3x+15x2−4:x+5x−2=3x+15x2−4⋅x−2x+5=3(x+5)(x−2)(x+2)⋅x−2x+5=3x+2.
Câu 13 :
Rút gọn biểu thức x4+4x2+55x3+5⋅2xx2+4⋅3x3+3x4+4x2+5 ta được:
Đáp án : B Phương pháp giải :
Ta biến đổi để rút gọn các phân thức rồi thực hiện phép tính nhân phân thức. Lời giải chi tiết :
x4+4x2+55x3+5⋅2xx2+4⋅3x3+3x4+4x2+5=x4+4x2+55(x3+1)⋅2xx2+4⋅3(x3+1)x4+4x2+5=6x5(x2+4).
Câu 14 :
Biểu thức P=x−12−x:x−1x+2⋅x−24−x2 có kết quả rút gọn là:
Đáp án : D Phương pháp giải :
Áp dụng quy tắc chia, nhân các phân thức đại số, thứ tự thực hiện dãy phép tính. Lời giải chi tiết :
P=x−12−x:x−1x+2⋅x−24−x2=x−12−x⋅x+2x−1⋅−(2−x)(x+2)(2−x)=−12−x=1x−2
Câu 15 :
Tìm biểu thức Q, biết: 5xx2+2x+1⋅Q=xx2−1
Đáp án : D Phương pháp giải :
+ Áp dụng quy tắc tìm phân thức chưa biết khi biết tích và thừa số + Thực hiện phép chia hai phân thức. + Chú ý đến các hằng đẳng thức để phân tích mẫu thức thành nhân tử Lời giải chi tiết :
5xx2+2x+1⋅Q=xx2−1⇒Q=xx2−1:5xx2+2x+1=xx2−1⋅x2+2x+15x=x(x−1)(x+1)⋅(x+1)25x=x+15(x−1)
Câu 16 :
Tìm x, biết: 1x⋅xx+1⋅x+1x+2⋅x+2x+3⋅x+3x+4⋅x+4x+5⋅x+5x+6=1
Đáp án : D Phương pháp giải :
+ Tìm điều kiện + Vận dụng quy tắc nhân phân thức, từ đó tìm được x. Lời giải chi tiết :
Điều kiện: x≠{0;−1;−2;−3;−4;−5;−6} 1x⋅xx+1⋅x+1x+2⋅x+2x+3⋅x+3x+4⋅x+4x+5⋅x+5x+6=1⇔1x+6=1⇒x+6=1⇔x=−5(KTM) Vậy phương trình vô nghiệm.
Chú ý
Một số em không tìm điều kiện nên chọn sai đáp án.
Câu 17 :
Thực hiện phép tính x−6x2+1⋅3x2−3x+3x2−36+x−6x2+1⋅3xx2−36 ta được kết quả là
Đáp án : D Phương pháp giải :
+ Áp dụng quy tắc nhân chia hai hay nhiều phân thức, áp dụng tính chất phân phối của phép nhân và phép cộng, thứ tự thực hiện phép tính. + Sau đó phân tích đa thức thành nhân tử và rút gọn. Lời giải chi tiết :
x−6x2+1⋅3x2−3x+3x2−36+x−6x2+1⋅3xx2−36 =x−6x2+1(3x2−3x+3x2−36+3xx2−36) =x−6x2+1⋅3x2−3x+3+3xx2−36 =x−6x2+1⋅3x2+3(x−6)(x+6) =x−6x2+1⋅3(x2+1)(x−6)(x+6)=3x+6.
Câu 18 :
Tìm biểu thức M, biết x+2yx3−8y3⋅M=5x2+10xyx2+2xy+4y2
Đáp án : B Phương pháp giải :
Áp dụng quy tắc tìm phân thức chưa biết A.M=B⇒M=A:B Sau đó sử dụng qui tắc nhân chia hai phân thức Thực hiện phân tích đa thức thành nhân tử và rút gọn. Lời giải chi tiết :
x+2yx3−8y3⋅M=5x2+10xyx2+2xy+4y2M=5x2+10xyx2+2xy+4y2:x+2yx3−8y3M=5x2+10xyx2+2xy+4y2⋅x3−8y3x+2yM=5x(x+2y)x2+2xy+4y2⋅(x−2y)(x2+2xy+4y2)x+2yM=5x(x−2y).
Câu 19 :
Thực hiện phép tính sau \left( {\dfrac{{2x}}{{3x + 1}} - 1} \right):\left( {1 - \dfrac{{8{x^2}}}{{9{x^2} - 1}}} \right), ta được kết quả là:
Đáp án : A Phương pháp giải :
+ Thực hiện quy đồng mẫu các phân thức trong từng ngoặc + Thực hiện nhân chia hai phân thức sau đó phân tích tử thức và mẫu thức thành nhân tử để rút gọn. Lời giải chi tiết :
\begin{array}{l}\left( {\dfrac{{2x}}{{3x + 1}} - 1} \right):\left( {1 - \dfrac{{8{x^2}}}{{9{x^2} - 1}}} \right) = \left( {\dfrac{{2x - 3x - 1}}{{3x + 1}}} \right):\left( {\dfrac{{9{x^2} - 1 - 8{x^2}}}{{9{x^2} - 1}}} \right)\\ = \dfrac{{ - x - 1}}{{3x + 1}}:\dfrac{{{x^2} - 1}}{{9{x^2} - 1}} = \dfrac{{ - x - 1}}{{3x + 1}}.\dfrac{{9{x^2} - 1}}{{{x^2} - 1}}\\ = \dfrac{{ - (x + 1)}}{{3x + 1}}.\dfrac{{(3x + 1)(3x - 1)}}{{(x + 1)(x - 1)}} = \dfrac{{1 - 3x}}{{x - 1}}.\end{array}
Câu 20 :
Thực hiện phép tính C = \dfrac{{2{x^2} + 4x + 8}}{{{x^3} - 3{x^2} - x + 3}}:\dfrac{{{x^3} - 8}}{{(x + 1)(x - 3)}}
Đáp án : D Phương pháp giải :
Áp dụng qui tắc chia hai phân thức và phân tích tử thức, mẫu thức thành nhân tử để rút gọn biểu thức Lời giải chi tiết :
C = \dfrac{{2{x^2} + 4x + 8}}{{{x^3} - 3{x^2} - x + 3}}:\dfrac{{{x^3} - 8}}{{(x + 1)(x - 3)}} \begin{array}{l}C = \dfrac{{2({x^2} + 2x + 4)}}{{{x^2}(x - 3) - (x - 3)}}.\dfrac{{(x + 1)(x - 3)}}{{(x - 2)({x^2} + 2x + 4)}}\\\,\,\,\,\, = \dfrac{{2(x + 1)(x - 3)}}{{(x - 3)({x^2} - 1)(x - 2)}}\\\,\,\,\,\, = \dfrac{2}{{(x - 1)(x - 2)}}.\end{array} Vậy C = \dfrac{2}{{\left( {x - 1} \right)\left( {x - 2} \right)}}
Câu 21 :
Cho Q = \left( {\dfrac{{{x^2} + 3x}}{{{x^3} + 3{x^2} + 9x + 27}} + \dfrac{3}{{{x^2} + 9}}} \right):\left( {\dfrac{1}{{x - 3}} - \dfrac{{6x}}{{{x^3} - 3{x^2} + 9x - 27}}} \right). Rút gọn Q ta được.
Đáp án : D Phương pháp giải :
- Tìm điều kiện để phân thức có nghĩa - Phân tích các mẫu thức thành nhân tử - Qui đồng các phân thức và thu gọn biểu thức Lời giải chi tiết :
Q = \left( {\dfrac{{{x^3} + 3x}}{{{x^3} + 3{x^2} + 9x + 27}} + \dfrac{3}{{{x^2} + 9}}} \right):\left( {\dfrac{1}{{x - 3}} - \dfrac{{6x}}{{{x^3} - 3{x^2} + 9x - 27}}} \right) (ĐK: x \ne \pm 3) \begin{array}{l}Q = \left( {\dfrac{{{x^2} + 3x}}{{{x^3} + 3{x^2} + 9x + 27}} + \dfrac{3}{{{x^2} + 9}}} \right):\left( {\dfrac{1}{{x - 3}} - \dfrac{{6x}}{{{x^3} - 3{x^2} + 9x - 27}}} \right)\\\,\,\,\,\, = \left( {\dfrac{{{x^2} + 3x}}{{{x^2}(x + 3) + 9(x + 3)}} + \dfrac{3}{{{x^2} + 9}}} \right):\left( {\dfrac{1}{{x - 3}} - \dfrac{{6x}}{{{x^2}(x - 3) + 9(x - 3)}}} \right)\\\,\,\,\,\, = \dfrac{{{x^2} + 3x + 3x + 9}}{{\left( {{x^2} + 9} \right)\left( {x + 3} \right)}}:\dfrac{{{x^2} + 9 - 6x}}{{\left( {x - 3} \right)\left( {{x^2} + 9} \right)}}\\\,\,\,\,\,\, = \dfrac{{{{(x + 3)}^2}}}{{({x^2} + 9)(x + 3)}}.\dfrac{{(x - 3)({x^2} + 9)}}{{{{(x - 3)}^2}}}\\\,\,\,\,\,\, = \dfrac{{x + 3}}{{x - 3}}.\end{array} Cho biểu thức P = \dfrac{{10x}}{{{x^2} + 3x - 4}} - \dfrac{{2x - 3}}{{x + 4}} + \dfrac{{x + 1}}{{1 - x}} Câu 22
Rút gọn P ta được
Đáp án : C Phương pháp giải :
Sử dụng kiến thức: ĐKXĐ của phân thức; cộng, trừ phân thức đại số, phân tích đa thức thành nhân tử và thu gọn. Lời giải chi tiết :
ĐK: \left\{ \begin{array}{l}{x^2} + 3x - 4 \ne 0\\x + 4 \ne 0\\1 - x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 1} \right)\left( {x + 4} \right) \ne 0\\x \ne 1\\x \ne - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne - 4\end{array} \right.. \begin{array}{l}P = \dfrac{{10x}}{{{x^2} + 3x - 4}} - \dfrac{{2x - 3}}{{x + 4}} + \dfrac{{x + 1}}{{1 - x}}\\ = \dfrac{{10x}}{{\left( {x - 1} \right)\left( {x + 4} \right)}} - \dfrac{{2x - 3}}{{x + 4}} - \dfrac{{x + 1}}{{x - 1}}\\ = \dfrac{{10x - (2x - 3)(x - 1) - (x + 1)(x + 4)}}{{(x - 1)(x + 4)}}\\ = \dfrac{{10x - 2{x^2} + 2x + 3x - 3 - {x^2} - 4x - x - 4}}{{(x - 1)(x + 4)}}\\ = \dfrac{{ - 3{x^2} + 10x - 7}}{{(x - 1)(x + 4)}}\\ = - \dfrac{{ - (x - 1)(3x - 7)}}{{(x - 1)(x + 4)}}\\ = \dfrac{{ - 3x + 7}}{{x + 4}}.\end{array} Vậy P = \dfrac{{ - 3x + 7}}{{x + 4}} với x \ne 1;x \ne -4 Câu 23
Tính giá trị của P khi x = - 1.
Đáp án : C Phương pháp giải :
Sử dụng kết quả câu trước P = \dfrac{{ - 3x + 7}}{{x + 4}} với x \ne 1;x \ne -4 +) Xét xem giá trị của x có thỏa mãn ĐKXĐ hay không. +) Nếu x thỏa mãn thì thay giá trị của x vào biểu thức P vừa rút gọn được và tính giá trị biểu thức. Lời giải chi tiết :
Theo câu trước ta có: P = \dfrac{{ - 3x + 7}}{{x + 4}} với x \ne 1;x \ne -4 Khi x = - 1(t/m) \Rightarrow P = \dfrac{{ - 3.( - 1) + 7}}{{ - 1 + 4}} = \dfrac{{10}}{3} Vậy khi x = - 1 thì P = \dfrac{{10}}{3}. Câu 24
Tìm x \in \mathbb{Z} để P + 1 \in \mathbb{Z}.
Đáp án : B Phương pháp giải :
+) Tìm ĐKXĐ của P. +) Tách P về dạng P = a + \dfrac{b}{{MS}},\,\,a,\,\,b \in Z. +) Đề P \in Z thì \dfrac{b}{{MS}} \in Z \Leftrightarrow MS \in U\left( b \right). +) Tìm U(b) sau đó lập bảng, giải phương trình tìm x. +) Xét xem các giá trị của x có thỏa mãn ĐKXĐ của bài toán hay không rồi kết luận x. Lời giải chi tiết :
Theo câu trước ta có P = \dfrac{{ - 3x + 7}}{{x + 4}} với x \ne 1;x \ne -4, nên P + 1 = \dfrac{{ - 3x + 7}}{{x + 4}} + 1 = \dfrac{{ - 3x + 7 + x + 4}}{{x + 4}} = \dfrac{{ - 2x + 11}}{{x + 4}} = - 2 + \dfrac{{19}}{{x + 4}} x \in Z để P + 1 \in Z \Rightarrow \left( {x + 4} \right) \in U\left( {19} \right) = \left\{ { \pm 1;\, \pm 19} \right\} 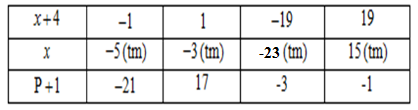 Vậy x \in \left\{ { - 23; - 5; - 3;15} \right\} thì P + 1 \in Z. Chú ý
Vì 1 \in Z nên để P+1 \in Z thì P \in Z nên các em có thể tìm x \in Z để P \in Z.
Câu 25 :
Cho x;y;z \ne 0 thỏa mãn x + y + z = 0. Chọn câu đúng về biểu thức A = \dfrac{{xy}}{{{x^2} + {y^2} - {z^2}}} + \dfrac{{yz}}{{{y^2} + {z^2} - {x^2}}} + \dfrac{{zx}}{{{z^2} + {x^2} - {y^2}}}.
Đáp án : D Phương pháp giải :
+ Sử dụng giả thiết để tính x^2+y^2-z^2 theo xy, y^2+z^2-x^2 theo yz và x^2+z^2-y^2 theo xz. + Từ đó có biểu thức đơn giản hơn để ta rút gọn và tính toán Lời giải chi tiết :
Từ x + y + z = 0 \Rightarrow x + y = - z \Rightarrow {x^2} + 2xy + {y^2} = {z^2} \Rightarrow {x^2} + {y^2} - {z^2} = - 2xy. Tương tự ta có : \left\{ \begin{array}{l}{y^2} + {z^2} - {x^2} = - 2yz\\{z^2} + {x^2} - {y^2} = - 2zx\end{array} \right. Do đó: A = \dfrac{{xy}}{{ - 2xy}} + \dfrac{{yz}}{{ - 2yz}} + \dfrac{{zx}}{{ - 2zx}} = - \dfrac{1}{2} - \dfrac{1}{2} - \dfrac{1}{2} = - \dfrac{3}{2} Vậy A = - \dfrac{3}{2}. Suy ra A < - 1.
Câu 26 :
Giá trị lớn nhất của phân thức \dfrac{5}{{{x^2} - 6x + 10}} là :
Đáp án : A Phương pháp giải :
- Biến đổi mẫu thức đã cho về dạng {(A + B)^2} + C - Đánh giá biểu thức, từ đó tìm GTLN của biểu thức. Lời giải chi tiết :
Ta có: \dfrac{5}{{{x^2} - 6x + 10}} = \dfrac{5}{{{x^2} - 6x + 9 + 1}} = \dfrac{5}{{{{(x - 3)}^2} + 1}} Vì {(x - 3)^2} \ge 0 \Rightarrow {(x - 3)^2} + 1 \ge 1 \Rightarrow \dfrac{1}{{{{(x - 3)}^2} + 1}} \le 1 \Rightarrow \dfrac{5}{{{{(x - 3)}^2} + 1}} \le 5 Vậy GTLN của phân thức là 5. Dấu “=” xảy ra khi {\left( {x - 3} \right)^2} = 0 hay x = 3.
|












