Bài tập trắc nghiệm Toán 8

Trắc nghiệm Bài 8: Đối xứng tâm Toán 8

Làm đề thi

Đề bài

Câu 1 :

Hãy chọn câu sai:

A

Điểm đối xứng với điểm $M$ qua $M$ cũng chính là điểm $M$ .
B

Hai điểm $A$ và $B$ gọi là đối xứng với nhau qua điểm $O$ khi $O$ là trung điểm của đoạn thẳng $AB$ .
C

Hình bình hành có một tâm đối xứng.
D

Đoạn thẳng có hai tâm đối xứng.

Câu 2 :

Hãy chọn câu sai:

A

Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo.
B

Đường tròn có tâm đối xứng chính là tâm của đường tròn.
C

Hình thang có tâm đối xứng là giao điểm của hai đường chéo.
D

Hình vuông có tâm đối xứng là giao điểm hai đường chéo.

Câu 3 :

Cho hình bình hành $ABEF$ . Gọi $O$ là giao điểm của $AE$ và $BF$ . Trong các khẳng định sau:

1. $E$ và $A$ đối xứng nhau qua $O$ .

2. $B$ và $F$ đối xứng nhau qua $O$ .

3. $E$ và $F$ đối xứng nhau qua $O$ .

4. $AB$ và $EF$ đối xứng nhau qua $O$ .

Có bao nhiêu khẳng định đúng ?

A

$1$
B

$2$
C

$3$
D

$4$

Câu 4 :

Tam giác $ABC$ đối xứng với tam giác $A'B'C'$ qua $O$ . Biết chu vi của tam giác $A'B'C'$ là $32\,cm$ . Chu vi của tam giác $ABC$ là :

A

$32\,dm$ .
B

$64\,cm$ .
C

$16\,cm$ .
D

$32\,cm$ .

Câu 5 :

Cho tam giác $ABC$ , trong đó $AB = 15cm,\,BC = 12cm$ . Vẽ hình đối xứng với tam giác $ABC$ qua trung điểm của cạnh $AC$ . Chu vi của tứ giác tạo thành là:

A

$54cm$ .
B

$53cm$ .
C

$52cm$ .
D

$51cm$ .

Câu 6 :

Hãy chọn câu đúng. Cho hình bình hành $ABCD$ . Lấy điểm $E$ thuộc tia đối của tia $AD$ sao cho $AD = AE$ , lấy $F$ thuộc tia đối của tia $CD$ sao cho $CD = CF$ . Hình bình hành $ABCD$ có thêm điều kiện gì để $E$ đối xứng với $F$ qua đường thẳng $DB$ ?

A

$AC = DB$ .
B

$\hat A = 90^\circ$ .
C

$AC \bot DB$ .
D

$\hat D = 90^\circ$ .

Câu 7 :

Cho tam giác $ABC$ , đường cao $AH$ , trong đó $BC = 18\,cm,AH = 3\,cm$ . Vẽ hình đối xứng với tam giác $ABC$ qua trung điểm của cạnh $BC$ . Diện tích của tam giác tạo thành là:.

A

$24\,c{m^2}$ .
B

$54\,c{m^2}$ .
C

$20\,c{m^2}$ .
D

$27\,c{m^2}$ .

Cho tam giác $ABC$ , trọng tâm $G$ . Gọi $N,P$ theo thứ tự là các điểm đối xứng của $B,C$ qua trọng tâm $G$ .

Câu 8

Tứ giác $BPNC$ là hình gì?

A.

Hình thang.
B.

Hình bình hành.
C.

Hình thang cân.
D.

Hình thang vuông.

Câu 9

Lấy $M$ là điểm đối xứng với $A$ qua $G.$ Chọn khẳng định đúng.

A.

$\Delta ABC = \Delta MNP$
B.

Tam giác $MNP$ đều
C.

Cả A, B đều sai.
D.

Cả A, B đều đúng.

Cho hình bình hành $ABCD$ có tâm đối xứng là $O$ , $E$ là điểm bất kỳ trên đoạn $OD.$ Gọi $F$ là điểm đối xứng của điểm $C$ qua $E$ .

Câu 10

Tứ giác $ODFA$ là hình gì?

A.

Hình thang.
B.

Hình bình hành.
C.

Hình thang cân.
D.

Hình thang vuông.

Câu 11

Xác định vị trí điểm $E$ trên $OD$ để hình thang $ODFA$ là hình bình hành.

A.

$E$ là chân đường vuông góc kẻ từ $C$ đến $OD$ .
B.

$E$ là trung điểm của $OD$ .
C.

Cả A, B đều sai.
D.

Cả A, B đều đúng.

Câu 12 :

Cho hình bình hành $ABCD$ , $O$ là giao điểm của hai đường chéo. Một đường thẳng đi qua $O$ cắt các cạnh $AB$ và $CD$ theo thứ tự ở $M$ và $N$ . Chọn khẳng định đúng.

A

Điểm $M$ đối xứng với điểm $N$ qua $O$ .
B

Điểm $M$ đối xứng với điểm $O$ qua $N$ .
C

Điểm $N$ đối xứng với điểm $O$ qua $M$ .
D

Điểm $A$ đối xứng với điểm $B$ qua $M$ .

Lời giải và đáp án

Câu 1 :

Hãy chọn câu sai:

A

Điểm đối xứng với điểm $M$ qua $M$ cũng chính là điểm $M$ .
B

Hai điểm $A$ và $B$ gọi là đối xứng với nhau qua điểm $O$ khi $O$ là trung điểm của đoạn thẳng $AB$ .
C

Hình bình hành có một tâm đối xứng.
D

Đoạn thẳng có hai tâm đối xứng.

Đáp án : D

Lời giải chi tiết :

+ Theo định nghĩa hai điểm đối xứng qua một điểm: Hai điểm $A$ , $B$ gọi là đối xứng với nhau qua điểm $O$ nếu $O$ là trung điểm của đoạn thẳng nối hai điểm đó nên B đúng.

+ Trung điểm của đoạn thẳng là tâm đối xứng duy nhất của đoạn thẳng đó nên D sai.

+ Hình bình hành có một tâm đối xứng là giao hai đường chéo, nên C đúng.

+ Điểm đối xứng của một điểm $M$ qua $M$ chính là $M$ nên A đúng.

Câu 2 :

Hãy chọn câu sai:

A

Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo.
B

Đường tròn có tâm đối xứng chính là tâm của đường tròn.
C

Hình thang có tâm đối xứng là giao điểm của hai đường chéo.
D

Hình vuông có tâm đối xứng là giao điểm hai đường chéo.

Đáp án : C

Lời giải chi tiết :

+ Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó nên A đúng.

+ Đường tròn là hình có tâm đối xứng là tâm của đường tròn nên B đúng.

+ Giao điểm hai đường chéo của hình vuông là tâm đối xứng của hình vuông đó nên D đúng.

+ Hình thang không có tâm đối xứng nên C sai.

Câu 3 :

Cho hình bình hành $ABEF$ . Gọi $O$ là giao điểm của $AE$ và $BF$ . Trong các khẳng định sau:

1. $E$ và $A$ đối xứng nhau qua $O$ .

2. $B$ và $F$ đối xứng nhau qua $O$ .

3. $E$ và $F$ đối xứng nhau qua $O$ .

4. $AB$ và $EF$ đối xứng nhau qua $O$ .

Có bao nhiêu khẳng định đúng ?

A

$1$
B

$2$
C

$3$
D

$4$

Đáp án : C

Lời giải chi tiết :

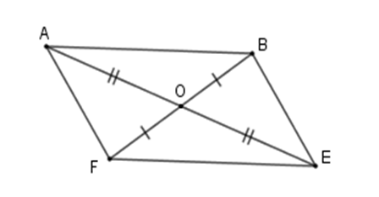Hình bình hành $ABCD$ có $OA = OE;\,OB = OF$ nên

+ $E$ và $A$ đối xứng nhau qua $O$ .

+ $B$ và $F$ đối xứng nhau qua $O$ .

+ $AB$ và $EF$ đối xứng nhau qua $O$ .

Nhưng $E$ và $F$ không đối xứng nhau qua $O$ vì $OE \ne OF;\,O$ không thuộc $EF$ .

Vậy có $3$ khẳng định đúng.

Câu 4 :

Tam giác $ABC$ đối xứng với tam giác $A'B'C'$ qua $O$ . Biết chu vi của tam giác $A'B'C'$ là $32\,cm$ . Chu vi của tam giác $ABC$ là :

A

$32\,dm$ .
B

$64\,cm$ .
C

$16\,cm$ .
D

$32\,cm$ .

Đáp án : D

Phương pháp giải :

Sử dụng chú ý về hai hình đối xứng với nhau qua một điểm.

“Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.”

Lời giải chi tiết :

Vì tam giác $ABC$ đối xứng với tam giác $A'B'C'$ qua $O$ nên $\Delta ABC = \Delta A'B'C'$ $\Rightarrow AB = A'B';\,AC = A'C';\,BC = B'C'$

Nên $AB + AC + BC = A'B' + A'C' + B'C'$ $\Rightarrow {P_{ABC}} = {P_{A'B'C'}}$

Do đó chu vi tam giác $ABC$ là ${P_{ABC}} = 32\,cm$ .

Câu 5 :

Cho tam giác $ABC$ , trong đó $AB = 15cm,\,BC = 12cm$ . Vẽ hình đối xứng với tam giác $ABC$ qua trung điểm của cạnh $AC$ . Chu vi của tứ giác tạo thành là:

A

$54cm$ .
B

$53cm$ .
C

$52cm$ .
D

$51cm$ .

Đáp án : A

Phương pháp giải :

Sử dụng chú ý: “Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.”

để tìm các cặp cạnh bằng nhau từ đó suy ra chu vi tứ giác.

Lời giải chi tiết :

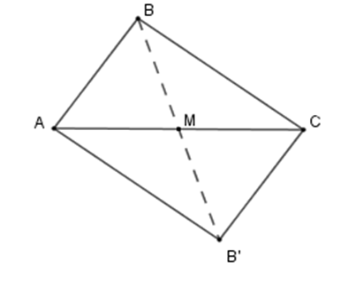Lấy $M$ là trung điểm $AC$ khi đó $A,\,C$ đối xứng nhau qua $M$ . Vẽ $B'$ đối xứng với $B$ qua $O$ . Khi đó tam giác $B'AC$ đối xứng với tam giác $ABC$ qua $M$ . Tứ giác tạo thành là $ABCB'$ .

Vì tam giác $B'AC$ đối xứng với tam giác $BCA$ qua $M$ nên $AB' = BC = 15\,cm;\,B'C= AB = 12\,cm$

Chu vi tứ giác $ABCB'$ là $AB + AC + CB' + AB'$ $= 12 + 15 + 12 + 15 = 54\,cm$ .

Câu 6 :

A

$AC = DB$ .
B

$\hat A = 90^\circ$ .
C

$AC \bot DB$ .
D

$\hat D = 90^\circ$ .

Đáp án : C

Phương pháp giải :

Bước 1: Sử dụng tính chất hình bình hành và đường trung bình của tam giác để suy ra $E$ đối xứng với $F$ qua điểm $B$ .

Bước 2: Để $E$ đối xứng với $F$ qua đường thẳng $BD$ ta cần thêm điều kiện $EF \bot BD$ từ đó suy ra điều kiện của hình bình hành $ABCD$ .

Lời giải chi tiết :

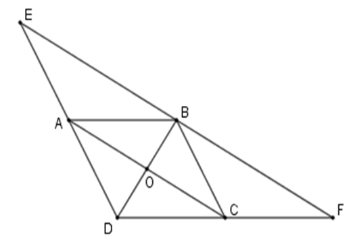Gọi $O$ là giao điểm hai đường chéo của hình bình hành $ABCD$ khi đó $OA = OC;\,OB = OD$

Xét tam giác $DBE$ ta có $OA$ là đường trung bình nên $OA{\rm{//}}EB;\,OA = \dfrac{1}{2}EB \Rightarrow AC{\rm{//}}EB;\,OA = \dfrac{1}{2}EB$ $\left( 1 \right)$

Tương tự $OC$ là đường trung bình của tam giác $BDF$ $\Rightarrow OC{\rm{//}}BF;\,OC = \dfrac{1}{2}FB \Rightarrow AC{\rm{//}}BF;\,OC = \dfrac{1}{2}FB$ $\left( 2 \right)$

Từ $\left( 1 \right);\,\left( 2 \right) \Rightarrow E;\,B;F$ thẳng hàng và $EB = BF$ (vì $OA = OC$ ) hay $E$ đối xứng với $F$ qua điểm $B$ .

Để $E$ đối xứng với $F$ qua đường thẳng $BD$ ta cần thêm điều kiện $EF \bot BD$ .

Mà $AC$ là đường trung bình của tam giác $DEF$ nên $AC{\rm{//}}\,EF$ suy ra $BD \bot AC$ .

Vậy hình bình hành $ABCD$ có thêm điều kiện hai đường chéo vuông góc thì $E$ đối xứng với $F$ qua đường thẳng $DB$ .

Câu 7 :

A

$24\,c{m^2}$ .
B

$54\,c{m^2}$ .
C

$20\,c{m^2}$ .
D

$27\,c{m^2}$ .

Đáp án : D

Phương pháp giải :

Sử dụng chú ý: “Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.”

từ đó suy ra diện tích tam giác.

Lời giải chi tiết :

Gọi tam giác $A'CB$ đối xứng với tam giác $ABC$ qua trung điểm cạnh $BC$ . Khi đó $\Delta ABC = \Delta A'CB$

Nên ${S_{ABC}} = {S_{A'BC}}$ .

Ta có ${S_{ABC}} = \dfrac{1}{2}AH.BC$ $= \dfrac{1}{2}.3.18 = 27\,c{m^2}$ nên ${S_{A'BC}} = 27\,c{m^2}$ .

Chú ý

Một số em nhầm công thức diện tích thành ${S_{ABC}} = AH.BC$ dẫn đến chọn B sai.

Cho tam giác $ABC$ , trọng tâm $G$ . Gọi $N,P$ theo thứ tự là các điểm đối xứng của $B,C$ qua trọng tâm $G$ .

Câu 8

Tứ giác $BPNC$ là hình gì?

A.

Hình thang.
B.

Hình bình hành.
C.

Hình thang cân.
D.

Hình thang vuông.

Đáp án : B

Phương pháp giải :

Sử dụng định nghĩa điểm đối xứng để suy ra tứ giác $BPNC$ có hai đường chéo giao nhau tại trung điểm mỗi đường nên $BPNC$ là hình bình hành.

Lời giải chi tiết :

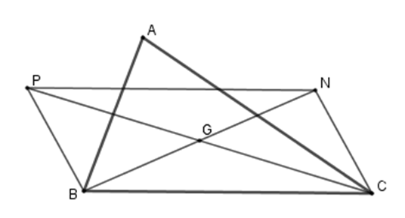Vì $N,P$ theo thứ tự là các điểm đối xứng của $B,C$ qua trọng tâm $G$ nên $G$ là trung điểm của $CP;\,BN$ .

Xét tứ giác $BPNC$ có hai đường chéo $CP$ và $BN$ giao nhau tại trung điểm mỗi đường nên $BPNC$ là hình bình hành (dhnb).

Câu 9

Lấy $M$ là điểm đối xứng với $A$ qua $G.$ Chọn khẳng định đúng.

A.

$\Delta ABC = \Delta MNP$
B.

Tam giác $MNP$ đều
C.

Cả A, B đều sai.
D.

Cả A, B đều đúng.

Đáp án : A

Phương pháp giải :

Bước 1: Chứng minh tương tự câu a) ta có $MNAB;\,PMCA$ là hình bình hành.

Bước 2: Sử dụng tính chất hình bình hành để suy ra các cặp cạnh bằng nhau. Từ đó suy ra các tam giác bằng nhau.

Lời giải chi tiết :

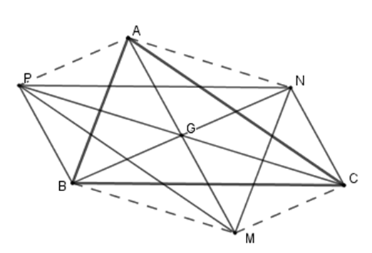Tương tự câu a) ta có tứ giác $MNAB$ là hình bình hành (do hai đường chéo giao nhau tại trung điểm $G$ mỗi đường) suy ra $MN = AB$ $\left( 1 \right)$ (tính chất hình bình hành).

Và tứ giác $PMCA$ là hình bình hành (do hai đường chéo giao nhau tại trung điểm $G$ mỗi đường) suy ra $PM = AC$ $\left( 2 \right)$ (tính chất hình bình hành).

Lại có $PN = BC$ $\left( 3 \right)$ (do $BPNC$ là hình bình hành (cmt))

Từ $\left( 1 \right);\,\left( 2 \right);\,\left( 3 \right)$ suy ra $\Delta ABC = \Delta MNP\,\left( {c - c - c} \right)$ mà tam giác $ABC$ không là tam giác đều (gt) nên $\Delta MNP$ không là tam giác đều.

Cho hình bình hành $ABCD$ có tâm đối xứng là $O$ , $E$ là điểm bất kỳ trên đoạn $OD.$ Gọi $F$ là điểm đối xứng của điểm $C$ qua $E$ .

Câu 10

Tứ giác $ODFA$ là hình gì?

A.

Hình thang.
B.

Hình bình hành.
C.

Hình thang cân.
D.

Hình thang vuông.

Đáp án : A

Phương pháp giải :

Sử dụng tính chất đường trung bình của tam giác để suy ra các cặp cạnh song song, từ đó có $ODFA$ là hình thang

Lời giải chi tiết :

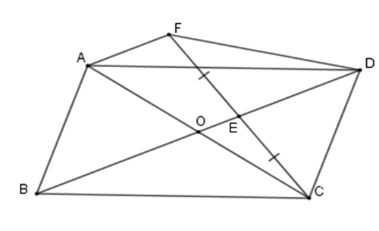+ Xét tam giác $CAF$ có $E$ là trung điểm của $CF$ ( do $F$ là điểm đối xứng của điểm $C$ qua $E$ ); $O$ là trung điểm $AC$ (do $O$ là tâm đối xứng của hình bình hành $ABCD$ ) nên $OE$ là đường trung bình của tam giác $CAF \Rightarrow OE = \dfrac{1}{2}AF;\,OE{\rm{//}}AF$ suy ra $OD\,{\rm{//}}\,AF \Rightarrow ODFA$ là hình thang.

Câu 11

Xác định vị trí điểm $E$ trên $OD$ để hình thang $ODFA$ là hình bình hành.

A.

$E$ là chân đường vuông góc kẻ từ $C$ đến $OD$ .
B.

$E$ là trung điểm của $OD$ .
C.

Cả A, B đều sai.
D.

Cả A, B đều đúng.

Đáp án : B

Phương pháp giải :

Để hình thang $ODFA$ là hình bình hành thì ta cần $OD = AF$ từ đó suy ra vị trí điểm $E$ trên $OD$ .

Lời giải chi tiết :

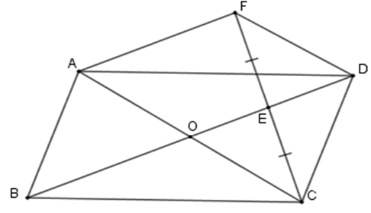Để hình thang $ODFA$ là hình bình hành thì ta cần $OD = AF$ mà $OE = \dfrac{1}{2}AF$ (cmt) nên $OE = \dfrac{1}{2}OD$

Hay $E$ là trung điểm của $OD$ .

Câu 12 :

A

Điểm $M$ đối xứng với điểm $N$ qua $O$ .
B

Điểm $M$ đối xứng với điểm $O$ qua $N$ .
C

Điểm $N$ đối xứng với điểm $O$ qua $M$ .
D

Điểm $A$ đối xứng với điểm $B$ qua $M$ .

Đáp án : A

Phương pháp giải :

Từ hai tam giác bằng nhau suy ra $O$ là trung điểm $MN$ nên $M$ đối xứng với điểm $N$ qua $O$

Lời giải chi tiết :

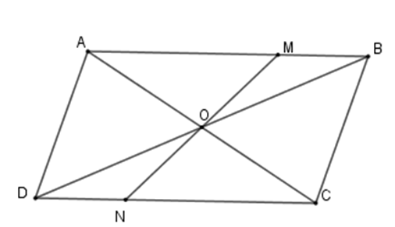Xét tam giác $\Delta OMB$ và $\Delta OND$ có

+ $\widehat {MOB} = \widehat {NOD}$ (đối đỉnh)

+ $OB = OD$ (tính chất hình bình hành)

+ $\widehat {MBO} = \widehat {NDO}$ (so le trong)

Nên $\Delta OMB = \Delta OND\,\left( {g - c - g} \right) \Rightarrow OM = ON$ (hai cạnh tương ứng)

Suy ra điểm $M$ đối xứng với điểm $N$ qua $O$ .

Bài liên quan

Trắc nghiệm Bài 9: Hình chữ nhật Toán 8

Luyện tập và củng cố kiến thức Bài 9: Hình chữ nhật Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 11: Hình thoi Toán 8

Luyện tập và củng cố kiến thức Bài 11: Hình thoi Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 12: Hình vuông Toán 8

Luyện tập và củng cố kiến thức Bài 12: Hình vuông Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài tập ôn tập chương 5 Toán 8

Luyện tập và củng cố kiến thức Bài tập ôn tập chương 5 Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Trắc nghiệm Bài 7: Hình bình hành Toán 8

Luyện tập và củng cố kiến thức Bài 7: Hình bình hành Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Trắc nghiệm Bài 8: Đối xứng tâm Toán 8

Trắc nghiệm Bài 9: Hình chữ nhật Toán 8

Trắc nghiệm Bài 11: Hình thoi Toán 8

Trắc nghiệm Bài 12: Hình vuông Toán 8

Trắc nghiệm Bài tập ôn tập chương 5 Toán 8

Trắc nghiệm Bài 7: Hình bình hành Toán 8