Trắc nghiệm Bài tập ôn tập chương 5 Toán 9Đề bài
Câu 1 :
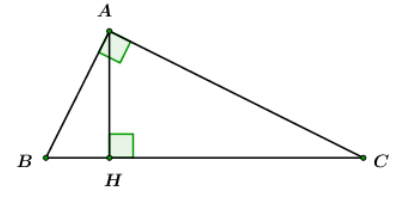
Cho tam giác ABC vuông tại A, chiều cao AH. Chọn câu sai.
Câu 2 :
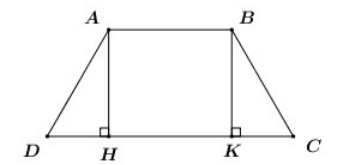
Cho hình vẽ sau: 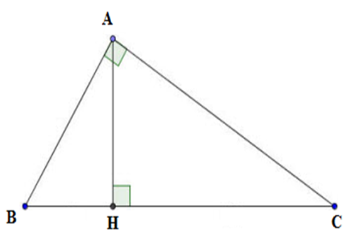 Chọn câu sai.
Câu 3 :
Chọn câu đúng nhất. Nếu α là một góc nhọn bất kỳ, ta có
Câu 4 :
Cho α;β là hai góc nhọn bất kì và α<β. Chọn câu đúng.
Câu 5 :
Tính giá trị của x trên hình vẽ 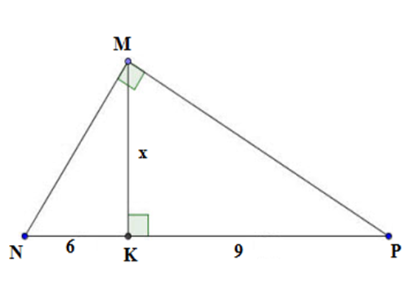
Câu 6 :
Cho tana=3. Khi đó cota bằng
Câu 7 :
Cho tam giác ABC vuông tại A có AB=3cm,BC=5cm.AH là đường cao. Tính BH,CH,AC và AH.
Câu 8 :
Giải tam giác vuông ABC, biết ˆA=90∘ và BC=50cm;ˆB=48o (làm tròn đến chữ số thập phân thứ nhất)
Câu 9 :
Cho tam giác ABC vuông tại A có AB=21cm; ˆC=40∘ , phân giác BD (D thuộc AC ). Độ dài phân giác BD là (Kết quả làm tròn đến chữ số thập phân thứ nhất)
Câu 10 :
Cho tam giác ABC vuông tại A, có AC=14,BC=17. Khi đó tanB bằng:
Câu 11 :
Giá trị biểu thức sin4α+cos4α+2sin2α.cos2α là
Câu 12 :
Cạnh bên của tam giác ABC cân tại A dài 20cm , góc ở đáy là 50∘
Câu 13 :
Cho hình vẽ, tìm x. 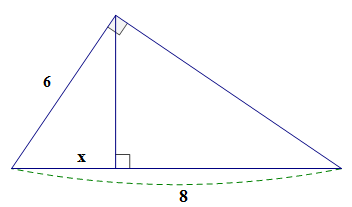
Câu 14 :
Cho tanα=34 . Giá trị biểu thức: M=sinα−2cosαsinα−cosα
Câu 15 :
Tìm x;y trong hình vẽ sau: 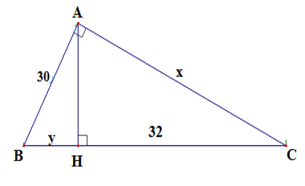
Câu 16 :
Tính số đo góc nhọn x, biết: cos2x−sin2x=12
Câu 17 :
Cho ΔABC vuông tại A. Biết ABAC=57. Đường cao AH=15cm. Tính HC.
Câu 18 :
Cho ΔABC vuông tại A,AB=12cm,AC=16cm, tia phân giác AD, đường cao AH. Tính HD.
Câu 19 :
Tính giá trị C=(3sinα+4cosα)2+(4sinα−3cosα)2
Câu 20 :
Cho biết tanα=23. Tính giá trị biểu thức: M=sin3α+3cos3α27sin3α−25cos3α
Câu 21 :
Sắp xếp theo thứ tự tăng dần cot700,tan330,cot550,tan280,cot400
Câu 22 :
Cho hình thang cân ABCD(AB∥CD); CD=2AD=2AB=8. Tính diện tích của hình thang đó.
Câu 23 :
Cho hình thang vuông ABCD có hai đáy AB=12cm,DC=16cm, cạnh xiên AD=8cm. Tính các góc và cạnh góc vuông của hình thang.
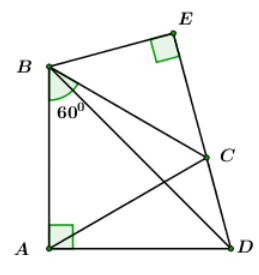
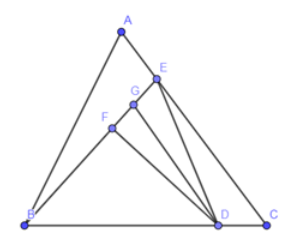
Cho tứ giác ABCD có AB=AC=AD=20cm,∠B=600 và ∠A=900. Kẻ BE⊥DC kéo dài.
Câu 24
Tính BE?
Câu 25
Tính CE.?
Câu 26
Tính CD?
Cho tam giác ABC vuông tại A, AB=15cm;AC=20cm. Phân giác của góc A cắt BC tại E.
Câu 27
Giải tam giác ABC
Câu 28
Tính BE;CE.
Câu 29 :
Bạn An đang học vẽ hình bằng phần mềm máy tính. An vẽ hình một ngôi nhà với phần mái có dạng hình tam giác cân (hình vẽ bên). Biết góc tạo bởi phần mái và mặt phẳng nằm ngang là 300, chiều dài mỗi bên dốc mái là 3,5m. Tính gần đúng bề rộng của mái nhà.
Cho tam giác ABC vuông tại A, AB=6cm,AC=4,5cm.
Câu 30
Tính các góc B, C và đường cao AH của tam giác.
Câu 31
Tính diện tích của tam giác ABC.
Cho tam giác ABC vuông tại A,∠B=350và AB=6cm. Vẽ đường cao AH và trung tuyến AM của tam giác ABC.
Câu 32
Giải tam giác vuông ABC.
Câu 33
Tính diện tích ΔAHM
Câu 34 :
Cho ΔABC vuông tại A có đường cao AHvà đường trung tuyến AM. Biết AH=3cm;HB=4cm. Hãy tính AB,AC,AM và diện tích tam giác ABC.
Câu 35 :
Cho tam giác ABC có AB=4cm,AC=4√3,BC=8cm. Tính số đo ∠B,∠C và độ dài đường cao AH của ΔABC.
Câu 36 :
Cho ΔMNP vuông tạiM có đường cao MH. Gọi I,K lần lượt là hình chiếu vuông góc của H trên MN,MP. Biết HK=9cm,HI=6cm. Khi đó tính độ dài các cạnh của ΔMNP.
Câu 37 :
Cho đoạn thẳng AB=2a và trung điểm O của nó. Trên nửa mặt phẳng bờ AB vẽ các tia Ax,By vuông góc với AB. Qua O vẽ một tia cắt tia Ax tại M sao cho ^AOM=α<900 . Qua O vẽ tia thứ hai cắt tia By tại N sao cho ^MON=90∘ . Khi đó, diện tích tam giác MON là
Câu 38 :
Cho tam giác ABC có diện tích là 900cm2. Điểm D ở giữa BC sao cho BC=5DC, điểm E ở giữa AC sao cho AC=4AE, hai điểm F,G ở giữa BE sao cho BE=6GF=6GE. Tính diện tích tam giác DGF.
Câu 39 :
Cho tam giác ABC vuông tại A. Tính A=sin2B+sin2C−tanB.tanC.
Lời giải và đáp án
Câu 1 :
Cho tam giác ABC vuông tại A, chiều cao AH. Chọn câu sai.
Đáp án : D Lời giải chi tiết :
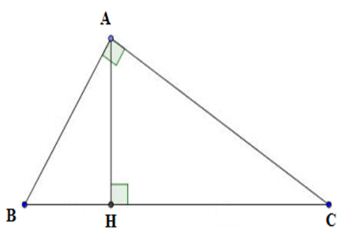 Ta thấy AH.BC=AB.AC nên D sai.
Câu 2 :
Cho hình vẽ sau:  Chọn câu sai.
Đáp án : D Lời giải chi tiết :
+ Xét tam giác AHB vuông tại H có sinB=AHAB nên A đúng. + Xét tam giác ABC vuông tại A có cosC=ACBC nên B đúng. + Xét tam giác ABC vuông tại A có tanB=ACAB nên C đúng. + Xét tam giác AHC vuông tại H có tanC=AHCH nên D sai.
Câu 3 :
Chọn câu đúng nhất. Nếu α là một góc nhọn bất kỳ, ta có
Đáp án : D Lời giải chi tiết :
Nếu α là một góc nhọn bất kỳ thì sin2α+cos2α=1;tanα.cotα=1 tanα=sinαcosα;cotα=cosαsinα nên cả A, B, C đều đúng
Câu 4 :
Cho α;β là hai góc nhọn bất kì và α<β. Chọn câu đúng.
Đáp án : C Lời giải chi tiết :
Với α;β là hai góc nhọn bất kì và α<β thì sinα<sinβ;cosα>cosβ;tanα<tanβ;cotα>cotβ. Vậy A, B, D sai, C đúng.
Câu 5 :
Tính giá trị của x trên hình vẽ 
Đáp án : C Phương pháp giải :
Sử dụng hệ thức lượng trong tam giác vuông: “ Bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông lên cạnh huyền” Lời giải chi tiết :
Xét tam giác MNP vuông tại M, có MK⊥NP ta có MK2=NK.PK (hệ thức lượng trong tam giác vuông) Hay x2=6.9⇔x2=54⇒x=3√6.
Câu 6 :
Cho tana=3. Khi đó cota bằng
Đáp án : A Phương pháp giải :
Sử dụng tana.cota=1 để tìm cota. Lời giải chi tiết :
Ta có tana.cota=1 nên cota=1tana=13.
Câu 7 :
Cho tam giác ABC vuông tại A có AB=3cm,BC=5cm.AH là đường cao. Tính BH,CH,AC và AH.
Đáp án : B Lời giải chi tiết :
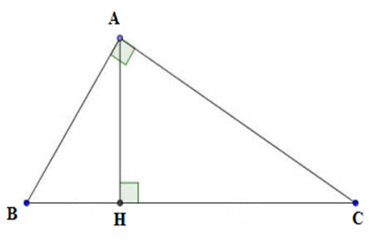 Xét tam giác ABC vuông tại A. + Theo định lý Pytago ta có A{B^2} + A{C^2} = B{C^2} \Leftrightarrow A{C^2} = {5^2} - {3^2} \Rightarrow AC = 4cm + Theo hệ thức lượng trong tam giác vuông ta có A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{3^2}}}{5} = \dfrac{9}{5} = 1,8cm Mà BH + CH = BC \Rightarrow CH = BC - BH = 5 - 1,8 = 3,2\,cm. Lại có AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{3.4}}{5} = 2,4cm Vậy BH = 1,8\,cm, CH = 3,2\,cm, AC = 4\,cm, AH = 2,4\,cm
Câu 8 :
Giải tam giác vuông ABC, biết \widehat A = 90^\circ \; và BC = 50cm;\widehat B = {48^o} (làm tròn đến chữ số thập phân thứ nhất)
Đáp án : D Phương pháp giải :
Giải tam giác vuông là tìm tất cả các cạnh và góc của tam giác vuông đó Sử dụng các tỉ số lượng giác, định lý về góc trong tam giác, hệ thức liên hệ giữa cạnh và góc trong tam giác vuông. Lời giải chi tiết :
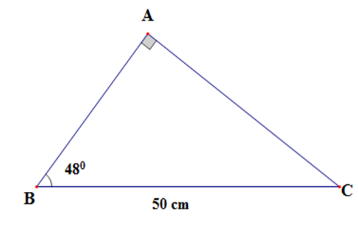 Xét \Delta ABC có: \widehat A = {90^o} AC = BC.\sin B = 50.\sin 48^\circ \approx 37,2cm AB = BC.\cos B = 50.\cos 48^\circ \approx 33,5cm Vậy AC \approx 37,2\,cm;\,AB \approx 33,5\,cm;\,\widehat C = 42^\circ .
Câu 9 :
Cho tam giác ABC vuông tại A có AB = 21\,cm; \widehat C = 40^\circ , phân giác BD (D thuộc AC ). Độ dài phân giác BD là (Kết quả làm tròn đến chữ số thập phân thứ nhất)
Đáp án : D Phương pháp giải :
+ Tính góc ABC từ đó suy ra góc ABD + Sử dụng hệ thức về cạnh và góc trong tam giác vuông ABD để tính BD. Lời giải chi tiết :
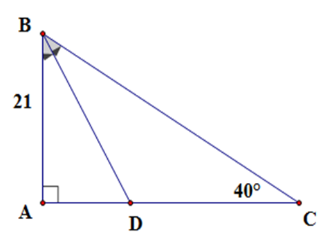 Xét tam giác ABC vuông tại A có \widehat {ABC} + \widehat C = 90^\circ \Rightarrow \widehat {ABC} = 50^\circ Mà BD là phân giác góc ABC nên \widehat {ABD} = \dfrac{1}{2}\widehat {ABC} = 25^\circ Xét tam giác ABD vuông tại A ta có BD = \dfrac{{AB}}{{\cos \widehat {ABD}}} = \dfrac{{21}}{{\cos 25^\circ }} \approx 23,2\,cm
Câu 10 :
Cho tam giác ABC vuông tại A, có AC = 14,BC = 17. Khi đó \tan B bằng:
Đáp án : C Phương pháp giải :
+ Tính AB theo định lý Pytago + Tính \tan B theo định nghĩa tỉ số lượng giác của góc nhọn. Lời giải chi tiết :
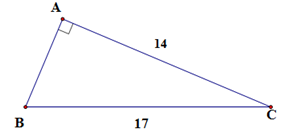 Xét tam giác ABC vuông tại A, theo định lý Pytago ta có A{B^2} + A{C^2} = B{C^2} \Rightarrow A{B^2} = {17^2} - {14^2} \Rightarrow AB = \sqrt {93} Lại có \tan B = \dfrac{{AC}}{{AB}} = \dfrac{{14}}{{\sqrt {93} }} = \dfrac{{14\sqrt {93} }}{{93}}
Câu 11 :
Giá trị biểu thức {\sin ^4}\alpha + {\cos ^4}\alpha + 2{\sin ^2}\alpha .{\cos ^2}\alpha là
Đáp án : A Phương pháp giải :
Biến đổi biểu thức đã cho thành hằng đẳng thức thứ nhất Sử dụng {\sin ^2}\alpha + {\cos ^2}\alpha = 1 để tính giá trị biểu thức Lời giải chi tiết :
Ta có {\sin ^4}\alpha + {\cos ^4}\alpha + 2{\sin ^2}\alpha .{\cos ^2}\alpha = {\left( {{{\sin }^2}\alpha } \right)^2} + 2{\sin ^2}\alpha .{\cos ^2}\alpha + {\left( {{{\cos }^2}\alpha } \right)^2} = {\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)^2} = {1^2} = 1 (vì {\sin ^2}\alpha + {\cos ^2}\alpha = 1)
Câu 12 :
Cạnh bên của tam giác ABC cân tại A dài 20cm , góc ở đáy là 50^\circ
Đáp án : B Phương pháp giải :
+ Kẻ đường cao AH. + Tính HB dựa vào quan hệ giữa cạnh và góc trong tam giác vuông + Lập luận dựa vào tính chất tam giác cân để tính cạnh đáy BC. Lời giải chi tiết :
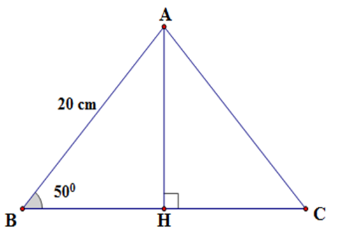 Kẻ AH \bot BC tại H. Suy ra H là trung điểm của BC (do tam giác ABC cân tại A có AH vừa là đường cao vừa là đường trung tuyến) Xét tam giác AHB vuông tại H có \cos \widehat {ABH} = \dfrac{{BH}}{{AB}} \Rightarrow BH = AB.\cos \widehat {ABH} = 20.\cos 50^\circ Mà H là trung điểm của BC nên BC = 2BH = 2.2.\cos 50^0\approx 25,7\,cm Vậy BC \approx 25,7\,cm.
Câu 13 :
Cho hình vẽ, tìm x. 
Đáp án : B Phương pháp giải :
Sử dụng hệ thức lượng trong tam giác vuông: “ bình phương cạnh góc vuông bằng tích hình chiếu của nó lên cạnh huyền với cạnh huyền” Lời giải chi tiết :
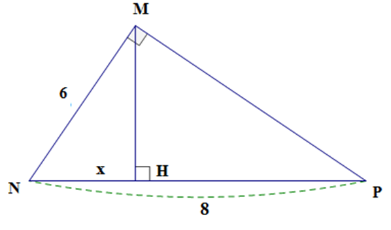 Đặt tên như hình vẽ trên. Tam giác MNP vuông tại M có MH \bot NP Theo hệ thức lượng trong tam giác vuông ta có M{N^2} = N{H^2}.NP \Rightarrow {6^2} = x.8 \Rightarrow x = 36:8 = 4,5. Vậy x = 4,5.
Câu 14 :
Cho \tan \alpha = \dfrac{3}{4} . Giá trị biểu thức: M = \dfrac{{\sin \alpha - 2\cos \alpha }}{{\sin \alpha - \cos \alpha }}
Đáp án : A Phương pháp giải :
Chia cả tử và mẫu của M cho \cos \alpha để xuất hiện \tan \alpha Thay \tan \alpha = \dfrac{3}{4} vào để tính M. Lời giải chi tiết :
Vì \tan \alpha = \dfrac{3}{4} nên \cos \alpha \ne 0. Chia cả tử và mẫu của M cho \cos \alpha ta được M = \dfrac{{\left( {\sin \alpha - 2\cos \alpha } \right):\cos \alpha }}{{\left( {\sin \alpha - \cos \alpha } \right):\cos \alpha }} = \dfrac{{\dfrac{{\sin \alpha }}{{\cos \alpha }} - 2}}{{\dfrac{{\sin \alpha }}{{\cos \alpha }} - 1}} = \dfrac{{\tan \alpha - 2}}{{\tan \alpha - 1}} Thay \tan \alpha = \dfrac{3}{4} vào M ta được M = \dfrac{{\dfrac{3}{4} - 2}}{{\dfrac{3}{4} - 1}} = 5.
Câu 15 :
Tìm x;y trong hình vẽ sau: 
Đáp án : D Phương pháp giải :
Áp dụng hệ thức lượng trong tam giác vuông A{B^2} = BH.BC;A{C^2} = CH.BC Lời giải chi tiết :
Ta có BC = BH + HC = y + 32 Áp dụng hệ thức lượng A{B^2} = BH.BC trong tam giác vuông ABC ta có \begin{array}{l}{30^2} = y\left( {y + 32} \right)\\ \Leftrightarrow {y^2} + 32y - 900 = 0\\ \Leftrightarrow {y^2} + 50y - 18y - 90 = 0\\ \Leftrightarrow y\left( {y + 50} \right) - 18\left( {y + 50} \right) = 0\\ \Leftrightarrow \left( {y - 18} \right)\left( {y + 50} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}y - 18 = 0\\y + 50 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}y = 18\left( N \right)\\y = - 50\,\left( L \right)\end{array} \right.\end{array} Suy ra y = 18 \Rightarrow BC = 18 + 32 = 50 Áp dụng hệ thức lượng A{C^2} = CH.BC ta có {x^2} = 32.50 \Leftrightarrow {x^2} = 1600 \Rightarrow x = 40. Vậy x = 40;y = 18.
Câu 16 :
Tính số đo góc nhọn x, biết: {\cos ^2}x - {\sin ^2}x = \dfrac{1}{2}
Đáp án : B Phương pháp giải :
Áp dụng hệ thức {\sin ^2}x + {\cos ^2}x = 1 để biến đổi giả thiết Lời giải chi tiết :
Ta có {\sin ^2}x + {\cos ^2}x = 1 \Rightarrow {\sin ^2}x = 1 - {\cos ^2}x Từ đó {\cos ^2}x - {\sin ^2}x = \dfrac{1}{2} \Leftrightarrow {\cos ^2}x - \left( {1 - {{\cos }^2}x} \right) = \dfrac{1}{2} \Leftrightarrow 2{\cos ^2}x = \dfrac{3}{2} \Leftrightarrow {\cos ^2}x = \dfrac{3}{4} \Rightarrow \cos x = \dfrac{{\sqrt 3 }}{2} (do x là góc nhọn nên \cos x > 0 ) Suy ra x = 30^\circ .
Câu 17 :
Cho \Delta ABC vuông tại A. Biết \dfrac{{AB}}{{AC}} = \dfrac{5}{7}. Đường cao AH = 15cm. Tính {\rm{ }}HC.
Đáp án : D Phương pháp giải :
Đặt AB = 5a;AC = 7a \left( {a > 0} \right) Sử dụng hệ thức lượng trong tam giác vuông một cách thích hợp để tìm HC. Lời giải chi tiết :
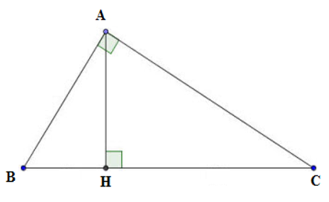 Vì \dfrac{{AB}}{{AC}} = \dfrac{5}{7} \Rightarrow AB = 5a;AC = 7a với a > 0. Theo hệ thức lượng trong tam giác ABC vuông tại A ta có \dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} \Leftrightarrow \dfrac{1}{{{{15}^2}}} = \dfrac{1}{{{{\left( {5a} \right)}^2}}} + \dfrac{1}{{{{\left( {7a} \right)}^2}}} \Leftrightarrow \dfrac{1}{{225}} = \dfrac{1}{{25{a^2}}} + \dfrac{1}{{49{a^2}}} \Leftrightarrow \dfrac{1}{{225}} = \dfrac{{74}}{{1225{a^2}}} \Rightarrow {a^2} = \dfrac{{666}}{{49}} \Rightarrow a = \dfrac{{3\sqrt {74} }}{7} Suy ra AB = \dfrac{{15\sqrt {74} }}{7};AC = 3\sqrt {74} Lại có AH.BC = AB.AC \Rightarrow BC = \dfrac{{AB.AC}}{{AH}} = \dfrac{{222}}{7} Mà A{C^2} = CH.BC \Rightarrow HC = \dfrac{{A{C^2}}}{{BC}} = 21\,cm.
Câu 18 :
Cho \Delta ABC vuông tại A,{\rm{ }}AB = {\rm{1}}2cm,{\rm{ }}AC = 16cm, tia phân giác AD, đường cao AH. Tính HD.
Đáp án : A Phương pháp giải :
Áp dụng tính chất đường phân giác của tam giác để tính BD. Áp dụng hệ thức lượng trong tam giác vuông để tính BH Từ đó tính HD. Lời giải chi tiết :
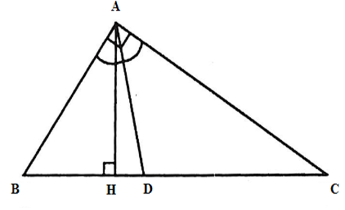 Xét tam giác vuông ABC ta có B{C^2} = A{B^2} + A{C^2} (định lý Pytago) Hay B{C^2} = {12^2} + {16^2} \Rightarrow B{C^2} = 400 \Rightarrow BC = 20\,cm Vì AD là phân giác góc A nên theo tính chất đường phân giác trong tam giác ta có \dfrac{{BD}}{{AB}} = \dfrac{{DC}}{{AC}} \Leftrightarrow \dfrac{{BD}}{{12}} = \dfrac{{DC}}{{16}} = \dfrac{{BD + DC}}{{12 + 16}} = \dfrac{{BC}}{{28}} = \dfrac{{20}}{{28}} = \dfrac{5}{7} Suy ra BD = 12.\dfrac{5}{7} = \dfrac{{60}}{7}\,cm Theo hệ thức lượng trong tam giác vuông ABC ta có A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{{12}^2}}}{{20}} = 7,2\,cm Lại có HD = BD - BH = \dfrac{{60}}{7} - 7,2 = \dfrac{{48}}{{35}}\,\,cm
Câu 19 :
Tính giá trị C = {(3\sin \alpha + 4\cos \alpha )^2} + {\left( {4\sin \alpha - 3\cos \alpha } \right)^2}
Đáp án : A Phương pháp giải :
Áp dụng hằng đẳng thức và đẳng thức {\sin ^2}\alpha + {\cos ^2}\alpha = 1 Lời giải chi tiết :
Ta có C = {(3\sin \alpha + 4\cos \alpha )^2} + {\left( {4\sin \alpha - 3\cos \alpha } \right)^2} = 9{\sin ^2}\alpha + 24\sin \alpha .\cos \alpha + 16{\cos ^2}\alpha + 16{\sin ^2}\alpha - 24\sin \alpha \cos \alpha + 9{\cos ^2}\alpha = 25{\sin ^2}\alpha + 25{\cos ^2}\alpha = 25\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) = 25.1 = 25 Vậy C = 25.
Câu 20 :
Cho biết \tan \alpha = \dfrac{2}{3}. Tính giá trị biểu thức: M = \dfrac{{{{\sin }^3}\alpha + 3{{\cos }^3}\alpha }}{{27{{\sin }^3}\alpha - 25{{\cos }^3}\alpha }}
Đáp án : D Phương pháp giải :
Chia cả tử và mẫu của M cho {\cos ^3}\alpha Thay \tan \alpha = \dfrac{2}{3} để tính M. Lời giải chi tiết :
Vì \tan \alpha = \dfrac{2}{3} nên \cos \alpha \ne 0. Chia cả tử và mẫu của M cho \cos^3 \alpha ta được M = \dfrac{{{{\sin }^3}\alpha + 3{{\cos }^3}\alpha }}{{27{{\sin }^3}\alpha - 25{{\cos }^3}\alpha }} = \dfrac{{\dfrac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} + 3\dfrac{{{{\cos }^3}\alpha }}{{{{\cos }^3}\alpha }}}}{{27\dfrac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} - 25\dfrac{{{{\cos }^3}\alpha }}{{{{\cos }^3}\alpha }}}} = \dfrac{{{{\tan }^3}\alpha + 3}}{{27{{\tan }^3}\alpha - 25}} Thay \tan \alpha = \dfrac{2}{3} ta được M = \dfrac{{{{\left( {\dfrac{2}{3}} \right)}^3} + 3}}{{27.{{\left( {\dfrac{2}{3}} \right)}^3} - 25}} = \dfrac{{ - 89}}{{459}}.
Câu 21 :
Sắp xếp theo thứ tự tăng dần \cot {70^0},{\rm{ tan}}\,{33^0},\cot {55^0},{\rm{ tan}}{28^0},{\rm{ cot}}{40^0}
Đáp án : C Phương pháp giải :
+ Sử dụng mối quan hệ: “Hai góc phụ nhau thì cotang góc này bằng tan góc kia” để đưa về cùng giá trị lượng giác \tan . + So sánh: Với \alpha ;\beta là hai góc nhọn bất kì và thì \tan \alpha < \tan \beta . Lời giải chi tiết :
Ta có \cot 70^\circ = \tan 20^\circ vì 70^\circ + 20^\circ = 90^\circ ; \cot \,55^\circ = \tan 35^\circ \,\, vì 55^\circ + 35^\circ = 90^\circ \cot 40^\circ = \tan 50^\circ vì 40^\circ + 50^\circ = 90^\circ Lại có 20^\circ < 28^\circ < 33^\circ < 35^\circ < 50^\circ hay \tan 20^\circ < \tan 28^\circ < \tan 33^\circ < \tan 35^\circ < \tan 50^\circ Suy ra \cot 70^\circ < \tan 28^\circ < \tan 33^\circ < \cot 55^\circ < \cot 40^\circ
Câu 22 :
Cho hình thang cân ABCD\,\,\,\left( {AB\parallel CD} \right); CD = 2AD = 2AB = 8. Tính diện tích của hình thang đó.
Đáp án : B Phương pháp giải :
- Kẻ AH,\,\,BK cùng vuông góc với CD \left( {H,\,\,K \in CD} \right). Chứng minh ABKH là hình chữ nhật. - Tính DH,\,\,CK. - Áp dụng định lí Pytago tính AH. - Tính diện tích hình thang: {S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AH}}{2}. Lời giải chi tiết :
Kẻ AH,\,\,BK cùng vuông góc với CD \left( {H,\,\,K \in CD} \right). Xét tứ giác ABKH có: \left\{ \begin{array}{l}AB\parallel HK\\AH\parallel BK\end{array} \right., suy ra ABKH là hình bình hành. Lại có \angle AHK = {90^0} nên ABKH là hình chữ nhật, do đó HK = AB = 4. Xét \Delta ADH và \Delta BCK có: \angle AHD = \angle BKC = {90^0}; AD = BC (tính chất hình thang cân); \angle ADH = \angle ACK (tính chất hình thang cân). \Rightarrow \Delta ADH = \Delta BCK (cạnh huyền – góc nhọn) \Rightarrow DH = CK (hai cạnh tương ứng). Mà DH + CK = CD - HK = 8 - 4 = 4. Do đó DH = CK = 2. Áp dụng định lí Pytago trong tam giác vuông ADH ta có: A{H^2} = A{D^2} - D{H^2} \Leftrightarrow A{H^2} = {4^2} - {2^2} = 12 \Leftrightarrow AH = 2\sqrt 3 . Vậy diện tích hình thang ABCD là: {S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AH}}{2} = \dfrac{{\left( {4 + 8} \right).2\sqrt 3 }}{2} = 12\sqrt 3 .
Câu 23 :
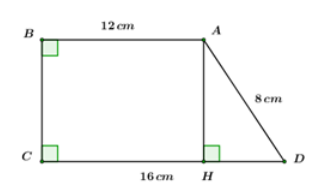
Cho hình thang vuông ABCD có hai đáy AB = 12\,cm,\,\,DC = 16\,\,cm, cạnh xiên AD = 8\,cm. Tính các góc và cạnh góc vuông của hình thang.
Đáp án : B Phương pháp giải :
Kẻ AH \bot CD = \left\{ H \right\},\,\,H \in CD. Sử dụng tính chất hình thang vuông, hình chữ nhật; định lý Pitago và hệ thức lượng giác trong tam giác vuông để tính. Lời giải chi tiết :
Kẻ AH \bot CD = \left\{ H \right\},\,\,H \in CD. Có hình thang vuông ABCD cạnh xiên AD \Rightarrow \angle ABC = \angle BCD = {90^o}. Dễ thấy ABCH là hình chữ nhật (có 3 góc vuông) \Rightarrow HC = AB = 12\,cm \Rightarrow HD = DC - HC = 16 - 12 = 4\,\,(cm) Áp dụng định lý Pitago cho \Delta AHD vuông tại H ta có: \begin{array}{l}A{H^2} = A{D^2} - H{D^2} \Rightarrow AH = \sqrt {A{D^2} - H{D^2}} = \sqrt {{8^2} - {4^2}} = 4\sqrt 3 \,\,\left( {cm} \right).\\ \Rightarrow BC = AH \approx 6,93\,\,cm\end{array} Xét \Delta AHD vuông tại H ta có: \cos \angle D = \dfrac{{HD}}{{AD}} = \dfrac{1}{2} \Rightarrow \angle D = {60^o} \begin{array}{l} \Rightarrow \angle DAH = {90^o} - \angle D = {30^o}\\ \Rightarrow \angle BAD = \angle BAH + \angle DAH = {90^o} + {30^o} = {120^o}.\end{array} Cho tứ giác ABCD có AB = AC = AD = 20\,\,cm,\,\,\angle B = {60^0} và \angle A = {90^0}. Kẻ BE \bot DC kéo dài.
Câu 24
Tính BE?
Đáp án : A Phương pháp giải :
Áp dụng định lý Pitago và các tỉ số lượng giác của góc nhọn để làm bài toán. Lời giải chi tiết :
Áp dụng định lý Pitago cho \Delta ABD vuông tại A ta có: DB = \sqrt {A{B^2} + A{D^2}} = \sqrt {{{20}^2} + {{20}^2}} = 20\sqrt 2 \,\,cm. Mà \Delta ABD có AB = AD = 20\,cm \Rightarrow \Delta ABD vuông cân tạiA. \Rightarrow \angle ABD = \angle ADB = {45^0} (tính chất tam giác cân). Theo đề bài ta có: \left\{ \begin{array}{l}AB = AC = 20\,cm\\\angle ABC = {60^0}\end{array} \right. \Rightarrow \Delta ABC là tam giác đều. \Rightarrow BC = 20\,cm;\,\,\,\angle BAC = \angle BCA = {60^0}. Lại có: AC = AD = 20\,\,cm \Rightarrow \Delta ACD cân tại A \begin{array}{l} \Rightarrow \angle ACD = \angle ADC = \dfrac{{{{180}^0} - \angle CAD}}{2} = \dfrac{{{{180}^0} - \left( {{{90}^0} - \angle BAC} \right)}}{2} = \dfrac{{{{180}^0} - \left( {{{90}^0} - {{60}^0}} \right)}}{2} = {75^0}.\\ \Rightarrow \angle EDB = \angle ADC - \angle ADB = {75^0} - {45^0} = {30^0}.\end{array} Xét \Delta BED vuông tại E ta có: \left\{ \begin{array}{l}BE = BD.\sin \angle EDB = 20\sqrt 2 .\sin {30^0} = 20\sqrt 2 .\dfrac{1}{2} = 10\sqrt 2 \,\,cm.\\ED = BD.cos\angle EDB = 20\sqrt 2 .cos{30^0} = 20\sqrt 2 .\dfrac{{\sqrt 3 }}{2} = 10\sqrt 6 \,\,cm.\end{array} \right. Câu 25
Tính CE.?
Đáp án : D Phương pháp giải :
Áp dụng định lý Pitago và các tỉ số lượng giác của góc nhọn để làm bài toán. Lời giải chi tiết :
Áp dụng định lý Pitago cho\Delta BEC vuông tại E ta có: \begin{array}{l}EC = \sqrt {B{C^2} - B{E^2}} = \sqrt {{{20}^2} - {{\left( {10\sqrt 2 } \right)}^2}} \\ = 10\sqrt 2 \,\,cm.\end{array} Câu 26
Tính CD?
Đáp án : C Phương pháp giải :
Áp dụng định lý Pitago và các tỉ số lượng giác của góc nhọn để làm bài toán. Lời giải chi tiết :
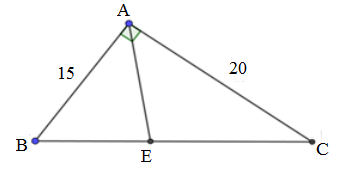
Ta có: CD = ED - EC = 10\sqrt 6 - 10\sqrt 2 = 10\sqrt 2 \left( {\sqrt 3 - 1} \right)\,\,\,cm \approx 10,35\,\,cm Cho tam giác ABC vuông tại A, AB{\rm{ }} = {\rm{ 15}}cm;AC = 20cm. Phân giác của góc A cắt BC tại E.
Câu 27
Giải tam giác ABC
Đáp án : B Phương pháp giải :
Sử dụng định lý Py-ta-go, tỉ số lượng giác của góc nhọn trong tam giác vuông. Lời giải chi tiết :
Áp dụng định lý Pytago cho \Delta ABC vuông tại A có: A{B^2} + A{C^2} = B{C^2} \Leftrightarrow B{C^2} = {15^2} + {20^2} = 625 \Rightarrow BC = 25 Xét \Delta ABC vuông tại A ta có: sinB = \dfrac{{AC}}{{BC}} = \dfrac{{20}}{{25}} \Rightarrow \angle B \approx {53^0}8' Vì \Delta ABC vuông tại A ta có: \angle B + \angle C = {90^0} \Leftrightarrow {53^0}8' + \angle C = {90^0} \Leftrightarrow \angle C \approx {36^0}52' Câu 28
Tính BE;CE.
Đáp án : C Phương pháp giải :
Sử dụng tính chất tia phân giác. Lời giải chi tiết :
Vì AE là tia phân giác góc A nên ta có: \Rightarrow \dfrac{{BE}}{{AB}} = \dfrac{{EC}}{{AC}} = \dfrac{{BE + EC}}{{AB + AC}} = \dfrac{{BC}}{{AB + AC}} = \dfrac{{25}}{{15 + 20}} = \dfrac{5}{7} \Rightarrow \left\{ \begin{array}{l}BE = \dfrac{5}{7}AB = \dfrac{5}{7}.15 = \dfrac{{75}}{7}\\EC = \dfrac{5}{7}AC = \dfrac{5}{7}.20 = \dfrac{{100}}{7}\end{array} \right..
Câu 29 :
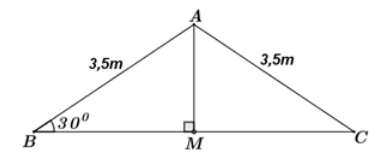
Bạn An đang học vẽ hình bằng phần mềm máy tính. An vẽ hình một ngôi nhà với phần mái có dạng hình tam giác cân (hình vẽ bên). Biết góc tạo bởi phần mái và mặt phẳng nằm ngang là {30^0}, chiều dài mỗi bên dốc mái là 3,5\,\,m. Tính gần đúng bề rộng của mái nhà.
Đáp án : B Phương pháp giải :
Áp dụng phương pháp tính cạnh trong tam giác vuông khi biết 1 góc và cạnh huyền. Lời giải chi tiết :
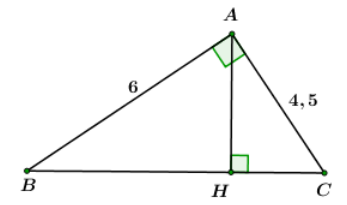
Ta vẽ lại mô hình mái nhà như hình vẽ bên. Theo đề bài cho ta có: \Delta ABC cân tại A AB = AC = 3,5m và \angle B = \angle C = {30^0} Thì khi đó bề rộng mái nhà chính là độ dài cạnh BC. Gọi M là trung điểm của BC. \Rightarrow AM là đường trung tuyến đồng thời là đường cao của \Delta ABC (tính chất). Xét \Delta ABM vuông tại M ta có: \cos B = \dfrac{{BM}}{{AB}} \Rightarrow cos\,{30^0} = \dfrac{{BM}}{{3,5}} \Rightarrow BM = \cos \,{30^0}.3,5 = \dfrac{{\sqrt 3 }}{2}.3,5 = \dfrac{{7\sqrt 3 }}{4}\,\,\,\left( m \right). \Rightarrow BC = 2BM\dfrac{{7\sqrt 3 }}{2}\,\,\left( m \right) \approx 6,06\,\,m. Vậy bề rộng mái nhà là 6,06\,m. Cho tam giác ABC vuông tại A, AB{\rm{ }} = {\rm{ 6}}cm,{\rm{ }}AC{\rm{ }} = 4,5cm.
Câu 30
Tính các góc B, C và đường cao AH của tam giác.
Đáp án : B Phương pháp giải :
Sử dụng định lý Pitago. Sử dụng định nghĩa tỉ số lượng giác Từ tỉ số lượng giác suy ra số đo góc Sử dụng hệ thức lượng trong tam giác vuông : AH.BC = AB.AC Lời giải chi tiết :
Áp dụng định lý Pitago cho \Delta ABC vuông tại A có: A{B^2} + A{C^2} = B{C^2} \Leftrightarrow B{C^2} = {6^2} + 4,{5^2} = 56,25 \Rightarrow BC = 7,5\,\,cm. Xét \Delta ABC vuông tại A ta có: sinB = \dfrac{{AC}}{{BC}} = \dfrac{{4,5}}{{7,5}} = \dfrac{3}{5} \Rightarrow \angle B \approx {36^0}52' Vì \Delta ABC vuông tại A ta có: \angle B + \angle C = {90^0} \Leftrightarrow {36^0}52' + \angle C = {90^0} \Leftrightarrow \angle C \approx {53^0}8' Áp dụng hệ thức lượng trong \Delta ABC vuông tại A có đường cao AH ta có: AH.BC = AB.AC \Leftrightarrow AH.7,5 = 4,5.6 \Leftrightarrow AH = 3,6 Câu 31
Tính diện tích của tam giác ABC.
Đáp án : A Phương pháp giải :
Sử dụng công thức tính diện tích tam giác Lời giải chi tiết :
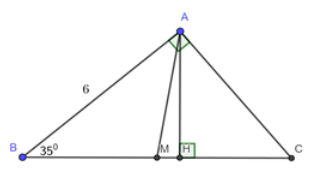
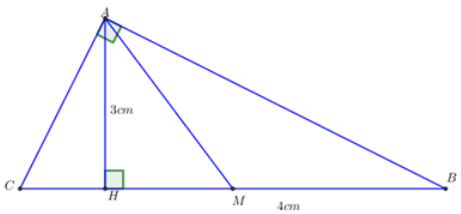
Ta có: {S_{\Delta ABC}} = \dfrac{1}{2}.AH.BC = \dfrac{1}{2}.3,6.7,5 = 13,5\,\,c{m^2}. Cho tam giác ABC vuông tại A,\angle B = {35^0}và AB{\rm{ }} = {\rm{ 6}}cm. Vẽ đường cao AH và trung tuyến AM của tam giác ABC.
Câu 32
Giải tam giác vuông ABC.
Đáp án : C Phương pháp giải :
Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông. Sử dụng tính chất hai góc phụ nhau. Lời giải chi tiết :
Xét \Delta ABC vuông tại A ta có: Câu 33
Tính diện tích \Delta AHM
Đáp án : A Phương pháp giải :
Sử dụng hệ thức lượng trong tam giác vuông. Áp dụng công thức tính diện tích tam giác. Lời giải chi tiết :
Vì AM là trung tuyến của tam giác ABC \Rightarrow M là trung điểm BC \Rightarrow BM = MC = \dfrac{{BC}}{2} \approx 3,66 Áp dụng hệ thức lượng cho \Delta ABC vuông tại A, có đường cao AH ta có: AH.BC = AB.AC \Leftrightarrow AH.7,32 = 6.4,2 \Leftrightarrow AH \approx 3,44 A{B^2} = BH.CB \Leftrightarrow {6^2} = BH.7,32 \Leftrightarrow BH \approx 4,92 Ta có: BM + MH = BH \Leftrightarrow MH = 4,92 - 3,66 \approx 1,26 {S_{\Delta AHM}} = \dfrac{1}{2}AH.MH \approx \dfrac{1}{2}.3,44.1,26 \approx 2,17\,\,\,\left( {đvdt} \right)
Câu 34 :
Cho \Delta ABC vuông tại A có đường cao AHvà đường trung tuyến AM. Biết AH = 3cm;\,HB = 4cm. Hãy tính AB,AC,AM và diện tích tam giác ABC.
Đáp án : A Phương pháp giải :
Sử dụng định lý Pytago, hệ thức lượng trong tam giác vuông và công thức tính diện tích tam giác. Lời giải chi tiết :
+) Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
Câu 35 :
Cho tam giác ABC có AB = 4cm,\,\,\,AC = 4\sqrt 3 ,\,\,BC = 8cm. Tính số đo \angle B,\,\,\angle C và độ dài đường cao AH của \Delta ABC.
Đáp án : D Phương pháp giải :
Áp dụng định lý Pitago đảo để chứng minh tam giác ABC vuông. Sử dụng tỉ số lượng giác của góc nhọn và hệ thức lượng trong tam giác vuông để làm bài toán. Lời giải chi tiết :
+) Chứng minh tam giác ABC vuông. Ta có: A{B^2} = {4^2} = 16;\,\,A{C^2} = {\left( {4\sqrt 3 } \right)^2} = 48;\,\,B{C^2} = {8^2} = 64. \Rightarrow A{B^2} + A{C^2} = 16 + 48 = 64 = B{C^2} \Rightarrow \Delta ABC vuông tại A (định lý Pitago đảo). +) Tính số đo \angle B,\,\,\angle C và độ dài đường cao AH của \Delta ABC. Áp dụng tỉ số lượng giác của góc nhọn trong \Delta ABC ta có: \begin{array}{l}\cos \angle B = \dfrac{{AB}}{{BC}} = \dfrac{4}{8} = \dfrac{1}{2} \Rightarrow \angle B = {60^0}\\ \Rightarrow \angle C = {180^0} - \angle B - \angle A = {180^0} - {60^0} - {90^0} = {30^0}.\end{array} Áp dụng hệ thức lượng trong \Delta ABC vuông tạiA và có đường cao AH ta có: AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{4.4\sqrt 3 }}{8} = 2\sqrt 3 \,\,cm. Vậy \angle B = {60^0},\,\,\,\angle C = {30^0},\,\,\,AH = 2\sqrt 3 \,\,cm.
Câu 36 :
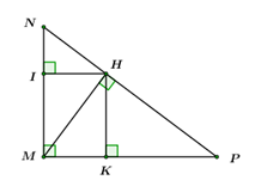
Cho \Delta MNP vuông tạiM có đường cao MH. Gọi I,\,\,K lần lượt là hình chiếu vuông góc của H trên MN,\,\,MP. Biết HK = 9\,cm,\,\,\,HI = 6\,cm. Khi đó tính độ dài các cạnh của \Delta MNP.
Đáp án : B Phương pháp giải :
Chứng minh tứ giác MKHI là hình chữ nhật từ đó ta tính được độ dài AH theo định lý Pitago. Sử dụng các công thức hệ thức lượng trong tam giác vuông điểm tìm các cạnh đề bài yêu cầu. Lời giải chi tiết :
Xét tứ giác MIHK ta có: \angle M = \angle I = \angle K = {90^0} \Rightarrow MIHK là hình chữ nhật (dhnb). \Rightarrow HI = MK = 6\,cm. Áp dụng định lý Pitago cho \Delta MHK vuông tại K ta có: M{H^2} = H{K^2} + M{K^2} = {6^2} + {9^2} = 117 \Rightarrow MH = \sqrt {117} . Áp dụng hệ thức lượng trong \Delta MHP vuông tại H có đường cao HK ta có: M{H^2} = MK.MP \Rightarrow MP = \dfrac{{M{H^2}}}{{MK}} = \dfrac{{117}}{6} = 19,5\,cm. Áp dụng hệ thức lượng trong \Delta MHN vuông tại H có đường cao HI ta có: M{H^2} = MI.MN \Rightarrow MN = \dfrac{{M{H^2}}}{{MI}} = \dfrac{{117}}{9} = 13\,cm. Áp dụng định lý Pitago cho \Delta MNP vuông tại N ta có: NP = \sqrt {M{N^2} + M{P^2}} = \sqrt {{{13}^2} + 19,{5^2}} = \dfrac{{13\sqrt {13} }}{2}\,\,cm. VậyMN = 13\,\,cm,\,\,MP = 19,5\,\,cm,\,\,NP = \dfrac{{13\sqrt {13} }}{2}\,\,cm.
Câu 37 :
Cho đoạn thẳng AB = 2a và trung điểm O của nó. Trên nửa mặt phẳng bờ AB vẽ các tia Ax,By\; vuông góc với AB. Qua O vẽ một tia cắt tia Ax tại M sao cho \widehat {AOM} = \alpha < {90^0} . Qua O vẽ tia thứ hai cắt tia By tại N sao cho \widehat {MON} = 90^\circ . Khi đó, diện tích tam giác MON là
Đáp án : A Phương pháp giải :
Áp dụng hệ thức về cạnh và góc trong tam giác vuông Áp dụng công thức tính diện tích tam giác vuông Lời giải chi tiết :
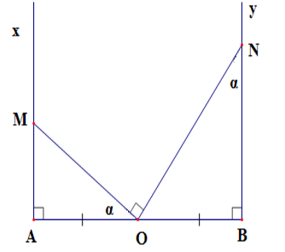 Theo đề bài ta có: AB = 2a \Rightarrow OA = OB = a Ta có: \widehat {ONB} = \widehat {AOM} = \alpha (cùng phụ với \widehat {BON} ) Xét \Delta AOM có \widehat A = 90^\circ OA = OM.\cos \alpha \Rightarrow OM = \dfrac{a}{{\cos \alpha }} OB = ON.\sin \alpha \Rightarrow ON = \dfrac{a}{{\sin \alpha }}
Câu 38 :
Cho tam giác ABC có diện tích là 900\,c{m^2}. Điểm D ở giữa BC sao cho BC = 5DC, điểm E ở giữa AC sao cho AC = 4AE, hai điểm F,G ở giữa BE sao cho BE = 6GF = 6GE. Tính diện tích tam giác DGF.
Đáp án : B Phương pháp giải :
Sử dụng tỉ số diện tích giữa hai tam giác. Lời giải chi tiết :
Ta kí hiệu: d(A;BC) là khoảng cách từ A đến đường thẳng BC (nghĩa là độ dài đoạn vuông góc kẻ từ A đến BC), tương tự với những kí hiệu khác trong bài. Ta có: \left\{ \begin{array}{l}{S_{\Delta DFG}} = \dfrac{1}{2}d\left( {D;\,\,FG} \right).FG\\{S_{\Delta DEB}} = \dfrac{1}{2}d\left( {D;\,\,FG} \right).BE\end{array} \right. \Rightarrow \dfrac{{{S_{\Delta DFG}}}}{{{S_{\Delta DEB}}}} = \dfrac{{FG}}{{BE}} = \dfrac{1}{6} \Rightarrow {S_{\Delta DFG}} = \dfrac{1}{6}{S_{\Delta DEB}}. \left\{ \begin{array}{l}{S_{\Delta DEB}} = \dfrac{1}{2}d\left( {D;\,\,BE} \right).BE\\{S_{\Delta BEC}} = \dfrac{1}{2}d\left( {C;\,\,BE} \right).BE\end{array} \right. \Rightarrow \dfrac{{{S_{\Delta DEB}}}}{{{S_{\Delta BEC}}}} = \dfrac{{d\left( {D;\,\,BE} \right)}}{{d\left( {C;\,\,BE} \right)}} = \dfrac{{BD}}{{BC}} = \dfrac{4}{5} \Rightarrow {S_{\Delta DEB}} = \dfrac{4}{5}{S_{\Delta BEC}}. \left\{ \begin{array}{l}{S_{\Delta BEC}} = \dfrac{1}{2}d\left( {B;\,\,EC} \right).EC\\{S_{\Delta ABC}} = \dfrac{1}{2}d\left( {B;\,\,AC} \right).AC\end{array} \right. \Rightarrow \dfrac{{{S_{\Delta BEC}}}}{{{S_{\Delta ABC}}}} = \dfrac{{EC}}{{AC}} = \dfrac{3}{4} \Rightarrow {S_{\Delta BEC}} = \dfrac{3}{4}{S_{\Delta ABC}}. \Rightarrow {S_{\Delta DFG}} = \dfrac{1}{6}.\dfrac{4}{5}.\dfrac{3}{4}.{S_{\Delta ABC}} = \dfrac{1}{{10}}.900 = 90\,c{m^2}.
Câu 39 :
Cho tam giác ABC vuông tại A. Tính A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C.
Đáp án : A Lời giải chi tiết :
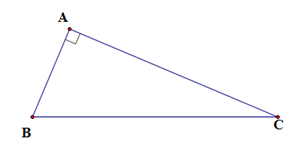 Ta có: \sin B = \dfrac{{AC}}{{BC}} \Rightarrow {\sin ^2}B = \dfrac{{A{C^2}}}{{B{C^2}}} \sin C = \dfrac{{AB}}{{BC}} \Rightarrow {\sin ^2}C = \dfrac{{A{B^2}}}{{B{C^2}}}\;\; \tan B = \dfrac{{AC}}{{AB}} ; \tan C = \dfrac{{AB}}{{AC}} Vậy A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\; = \dfrac{{A{C^2}}}{{B{C^2}}} + \dfrac{{A{B^2}}}{{B{C^2}}} - \dfrac{{AC}}{{AB}}.\dfrac{{AB}}{{AC}} = \dfrac{{A{C^2} + A{B^2}}}{{B{C^2}}} - 1 = \dfrac{{B{C^2}}}{{B{C^2}}} - 1 = 0 (vì theo định lý Pytago thì A{C^2} + A{B^2} = B{C^2} )
|