Bài tập trắc nghiệm Toán 9

Trắc nghiệm Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông Toán 9

Làm đề thi

Đề bài

Câu 1 :

Cho tam giác $MNP$ vuông tại $N$. Hệ thức nào sau đây là đúng?

  • A

    $MN = MP.\sin P$

  • B

    $MN = MP.\cos P$

  • C

    $MN = MP.\tan P$

  • D

    $MN = MP.\cot P$

Câu 2 :

Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c.\) Chọn khẳng định sai?

  • A

    \(b = a.\sin B = a.\cos C\)

  • B

    $a = c.\tan B = c.\cot C$

  • C

    ${a^2} = {b^2} + {c^2}$

  • D

    \(c = a.\sin C = a.\cos B\)

Câu 3 :

Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 10\,cm,\widehat C = 30^\circ .\) Tính $AB;BC$

  • A

    $AB = \dfrac{{5\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$

  • B

    $AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{14\sqrt 3 }}{3}$

  • C

    $AB = \dfrac{{10\sqrt 3 }}{3};BC = 20\sqrt 3 $

  • D

    $AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$

Câu 4 :

Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 12\,cm,\widehat B = 40^\circ .\) Tính $AC;\widehat C$ . (làm tròn đến chữ số thập phân thứ hai)

  • A

    $AC \approx 7,71;\widehat C = 40^\circ $

  • B

     $AC \approx 7,72;\widehat C = 50^\circ $

  • C

    $AC \approx 7,71;\widehat C = 50^\circ $

  • D

    $AC \approx 7,73;\widehat C = 50^\circ $

Câu 5 :

Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 15\,cm,AB = 12\,cm\) . Tính $AC;\widehat B$ .

  • A

    $AC = 8 (cm);\widehat B \approx 36^\circ 52'$

  • B

    $AC = 9(cm);\widehat B \approx 36^\circ 52'$

  • C

    $AC = 9(cm);\widehat B \approx 37^\circ 52'$     

  • D

    $AC = 9(cm);\widehat B \approx 36^\circ 55'$

Câu 6 :

Cho tam giác \(ABC\) có \(AB = 16,AC = 14\) và \(\widehat B = {60^0}\). Tính $BC$

  • A

    $BC = 10$

  • B

    $BC = 11$

  • C

    $BC = 9$

  • D

     $BC = 12$

Câu 7 :

Cho tam giác $ABC$ có $\widehat B = {60^0},\widehat C = {50^0},AC = 3,5cm.$ Diện tích tam giác $ABC$ gần nhất với giá trị nào dưới đây?

  • A

    $4$

  • B

    $5$

  • C

    $7$

  • D

    $8$

Câu 8 :

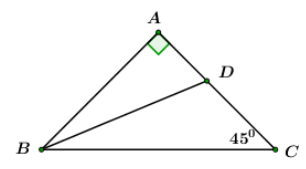
Cho tứ giác $ABCD$ có $\widehat A = \widehat D = {90^0},\widehat C = {40^0},AB = 4cm,AD = 3cm.$ Tính diện tích tứ giác $ABCD.$ (làm tròn đến chữ số thập phân thứ hai)

  • A

    $17,36\,\,c{m^2}$

  • B

    $17,4\,\,c{m^2}$

  • C

    $17,58\,\,c{m^2}$

  • D

    $17,54\,\,c{m^2}$

Câu 9 :

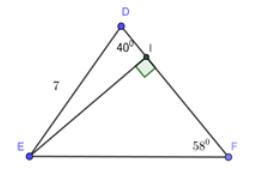
Cho tam giác \(DEF\) có \(DE = 7cm;\angle D = {40^0};\angle F = {58^0}\). Kẻ đường cao \(EI\) của tam giác đó.

Hãy tính:  (Kết quả làm tròn đến chữ số thập phân thứ 1)

Câu 9.1

Đường cao \(EI\)

  • A.
    \(EI = 4,5cm\)
  • B.
    \(EI = 5,4cm\)
  • C.
    \(EI = 5,9cm\)
  • D.
    \(EI = 5,6cm\)
Câu 9.2

Cạnh \(EF\)

  • A.
    \(EF = 4,5cm\)
  • B.
    \(EF = 5,3cm\)
  • C.
    \(EF = 5,9cm\)
  • D.
    \(EF = 6,2cm\)
Câu 10 :

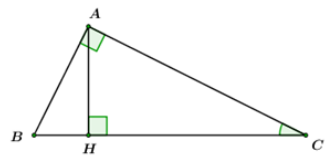
Cho tam giác $ABC$ có $BC = 11cm,\widehat {ABC} = 40^\circ $ và $\widehat {ACB} = {30^0}.$ Gọi $N$ là chân đường vuông góc hạ từ $A$ xuống cạnh $BC$.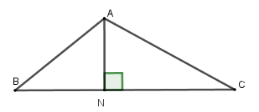 

Câu 10.1

Độ dài $AN$ gần nhất với giá trị nào dưới đây ?

  • A.

    $5$

  • B.

    $4$

  • C.

    $6$

  • D.

    $7$

Câu 10.2

Độ dài $AC$ gần nhất với giá trị nào dưới đây ?

  • A.

    $7$

  • B.

    $6$

  • C.

     $5$

  • D.

    $4$

Câu 10.3

Diện tích tam giác $ABC$ gần với giá trị nào dưới đây ?

  • A.

    $27$

  • B.

    $23$

  • C.

    $22$

  • D.

    $21$

Câu 11 :

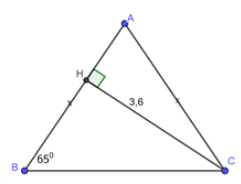
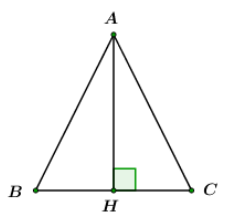
Cho tam giác \(ABC\) cân tại \(A,\,\,\angle B = {65^0},\)  đường cao \(CH = 3,6\).  Hãy giải tam giác \(ABC\).

  • A
    \(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 5,6\,\,;\,\,BC = 8,52\)
  • B
    \(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 5,6\,\,;\,\,BC = 4,42\)
  • C
    \(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 4,7\,\,;\,\,BC = 4,24\)
  • D
    \(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 4,7\,\,;\,\,BC = 3,97\)
Câu 12 :

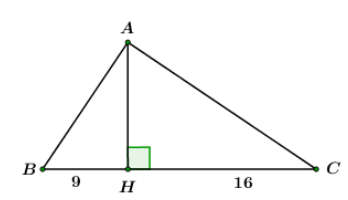
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\), biết \(HB = 9;HC = 16\). Tính góc \(B\) và góc \(C.\) 

  • A
    \(\angle B = {53^0}8'\,\,\,;\,\,\,\angle C = {36^0}52'\)
  • B
    \(\angle B = {36^0}52'\,\,\,;\,\,\,\angle C = {53^0}8'\)
  • C
    \(\angle B = {48^0}35'\,\,\,;\,\,\,\angle C = {41^0}25'\)
  • D
    \(\angle B = {41^0}25'\,\,\,;\,\,\,\angle C = {48^0}35'\)
Câu 13 :

Một tam giác cân có đường cao ứng với đáy đúng bằng độ dài đáy. Tính các góc của tam giác đó.

  • A
    \(\angle A = {45^0}\,\,;\,\,\,\angle B = \angle C = {67^0}30'\)
  • B
    \(\angle A = {30^0}\,\,;\,\,\,\angle B = \angle C = {75^0}\)
  • C
    \(\angle A = {48^0}6'\,\,;\,\,\,\angle B = \angle C = {65^0}57'\)
  • D
    \(\angle A = {53^0}8'\,\,;\,\,\,\angle B = \angle C = {63^0}26'\)
Câu 14 :

Cho tam giác \(ABC\) vuông cân tại \(A\left( {AB = AC = a} \right)\) . Phân giác của góc \(B\) cắt \(AC\) tại \(D\).

Tính \(DA;DC\) theo \(a\).

  • A
    \(AD = a.\cos 22,{5^0}\,\,;\,\,DC = a - a.\cos 22,{5^0}\)
  • B
    \(AD = a.\sin 22,{5^0}\,\,;\,\,DC = a - a.\sin 22,{5^0}\)
  • C
    \(AD = a.\tan 22,{5^0}\,\,;\,\,DC = a - a.\tan 22,{5^0}\)
  • D
    \(AD = a.\cot 22,{5^0}\,\,;\,\,DC = a - a.cot22,{5^0}\)
Câu 15 :

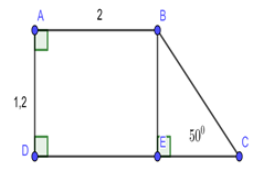
Cho hình thang \(ABCD\) vuông tại \(A\) và \(D;\)\(\angle C = {50^0}\). Biết \(AB = 2;AD = 1,2\). Tính diện tích hình thang \(ABCD.\)

  • A

    \({S_{ABCD}} = 2\,\,\,\left( {đvdt} \right)\)

  • B

    \({S_{ABCD}} = 3\,\,\,\left( {đvdt} \right)\)

  • C

    \({S_{ABCD}} = 4\,\,\,\left( {đvdt} \right)\)

  • D

    \({S_{ABCD}} = \dfrac{5}{2}\,\,\,\left( {đvdt} \right)\)

Câu 16 :

Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(AB = 3cm,\,\,AC = 4cm.\) Tính độ dài đường cao \(AH,\) tính \(\cos \angle ACB\).

  • A

    \(AH = 2,8cm\,\,\,;\,\,\,\cos \angle ACB = \dfrac{3}{5}\)

  • B

    \(AH = 2,4cm\,\,\,;\,\,\,\cos \angle ACB = \dfrac{4}{5}\)

  • C

    \(AH = 2,5cm\,\,\,;\,\,\,\cos \angle ACB = \dfrac{3}{4}\)

  • D

    \(AH = 1,8cm\,\,\,;\,\,\,\cos \angle ACB = \dfrac{2}{3}\)

Câu 17 :

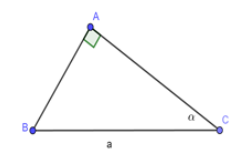
Cho tam giác \(ABC\) vuông tại \(A\); \(BC = a\) không đổi, \(\angle C = \alpha \,\,\,\left( {{0^0} < \alpha  < {{90}^0}} \right)\)

Câu 17.1

Lập công thức để tính diện tích tam giác ABC theo \(a\) và \(\alpha\) .

  • A.

    \(\dfrac{1}{2}{a^2}\sin \alpha .\cos \alpha \)

  • B.
    \({a^2}\sin \alpha .\cos \alpha \)
  • C.
    \(2{a^2}\sin \alpha .\cos \alpha \)
  • D.
    \(3{a^2}\sin \alpha .\cos \alpha \)
Câu 17.2

Tìm góc  để diện tích tam giác ABC là lớn nhất. Tính giá trị lớn nhất ấy.

  • A.

    \(\alpha  = {45^0}\,\,;\,\,\max {S_{\Delta ABC}} = \dfrac{1}{2}{a^2}\)

  • B.

    \(\alpha  = {30^0}\,\,;\,\,\max {S_{\Delta ABC}} = \dfrac{{\sqrt 3 }}{4}{a^2}\)

  • C.

    \(\alpha  = {60^0}\,\,;\,\,\max {S_{\Delta ABC}} = \dfrac{{\sqrt 3 }}{4}{a^2}\)

  • D.

    \(\alpha  = {45^0}\,\,;\,\,\max {S_{\Delta ABC}} = \dfrac{1}{4}{a^2}\)

Lời giải và đáp án

Câu 1 :

Cho tam giác $MNP$ vuông tại $N$. Hệ thức nào sau đây là đúng?

  • A

    $MN = MP.\sin P$

  • B

    $MN = MP.\cos P$

  • C

    $MN = MP.\tan P$

  • D

    $MN = MP.\cot P$

Đáp án : A

Lời giải chi tiết :

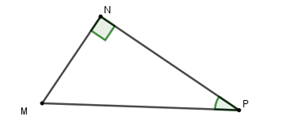Ta có $\sin P = \dfrac{{MN}}{{MP}} \Rightarrow MN = MP.\sin P$.

Câu 2 :

Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c.\) Chọn khẳng định sai?

  • A

    \(b = a.\sin B = a.\cos C\)

  • B

    $a = c.\tan B = c.\cot C$

  • C

    ${a^2} = {b^2} + {c^2}$

  • D

    \(c = a.\sin C = a.\cos B\)

Đáp án : B

Lời giải chi tiết :

Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c.\) Ta có :

+) Theo định lý Py-ta-go ta có ${a^2} = {b^2} + {c^2}$ nên C đúng

+) Theo hệ thức về cạnh và góc trong tam giác vuông ta có

\(b = a.\sin B = a.\cos C\); \(c = a.\sin C = a.\cos B\); \(b = c.\tan B = c.\cot C\); \(c = b.\tan C = b.\cot B\).

Nên A,D đúng.

Câu 3 :

Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 10\,cm,\widehat C = 30^\circ .\) Tính $AB;BC$

  • A

    $AB = \dfrac{{5\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$

  • B

    $AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{14\sqrt 3 }}{3}$

  • C

    $AB = \dfrac{{10\sqrt 3 }}{3};BC = 20\sqrt 3 $

  • D

    $AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$

Đáp án : D

Lời giải chi tiết :

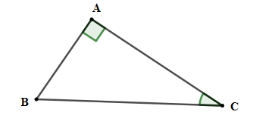Xét tam giác  \(ABC\) vuông tại \(A\) có

$\tan C = \dfrac{{AB}}{{AC}} \Rightarrow AB = AC.\tan C = 10.\tan 30^\circ  = \dfrac{{10\sqrt 3 }}{3}$; $\cos C = \dfrac{{AC}}{{BC}} \Rightarrow BC = \dfrac{{AC}}{{\cos C}} = \dfrac{{10}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{20\sqrt 3 }}{3}$

Vậy $AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$.

Câu 4 :

Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 12\,cm,\widehat B = 40^\circ .\) Tính $AC;\widehat C$ . (làm tròn đến chữ số thập phân thứ hai)

  • A

    $AC \approx 7,71;\widehat C = 40^\circ $

  • B

     $AC \approx 7,72;\widehat C = 50^\circ $

  • C

    $AC \approx 7,71;\widehat C = 50^\circ $

  • D

    $AC \approx 7,73;\widehat C = 50^\circ $

Đáp án : C

Phương pháp giải :

+Tính góc còn lại theo định lý về tổng ba góc trong tam giác

+) Sử dụng hệ thức về cạnh và góc trong tam giác vuông để tìm các cạnh .

Lời giải chi tiết :

Xét tam giác  \(ABC\) vuông tại \(A\) có

+) $\sin B = \dfrac{{AC}}{{BC}} \Rightarrow AC = BC.\sin B = 12.\sin 40^\circ  \approx 7,71$

+) $\widehat A + \widehat B + \widehat C = 180^\circ  \Rightarrow \widehat C = 180^\circ  - 40^\circ  - 90^\circ  = 50^\circ $

Vậy $AC \approx 7,71;\widehat C = 50^\circ $.

Câu 5 :

Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 15\,cm,AB = 12\,cm\) . Tính $AC;\widehat B$ .

  • A

    $AC = 8 (cm);\widehat B \approx 36^\circ 52'$

  • B

    $AC = 9(cm);\widehat B \approx 36^\circ 52'$

  • C

    $AC = 9(cm);\widehat B \approx 37^\circ 52'$     

  • D

    $AC = 9(cm);\widehat B \approx 36^\circ 55'$

Đáp án : B

Phương pháp giải :

+Tính cạnh còn lại theo định lý Py-ta-go

+) Tìm tỉ số lượng giác của góc từ đó suy ra góc.

Lời giải chi tiết :

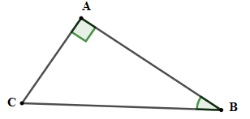Xét tam giác  \(ABC\) vuông tại \(A\) có

+) $B{C^2} = A{B^2} + A{C^2} \Rightarrow AC = \sqrt {B{C^2} - A{B^2}}  = \sqrt {{{15}^2} - {{12}^2}}  = 9 (cm)$

+) $\sin B = \dfrac{{AC}}{{BC}} = \dfrac{9}{{15}} = \dfrac{3}{5}$

$\Rightarrow \widehat B \approx 36^\circ 52'$

Vậy $AC = 9 (cm);\widehat B \approx 36^\circ 52'$.

Câu 6 :

Cho tam giác \(ABC\) có \(AB = 16,AC = 14\) và \(\widehat B = {60^0}\). Tính $BC$

  • A

    $BC = 10$

  • B

    $BC = 11$

  • C

    $BC = 9$

  • D

     $BC = 12$

Đáp án : A

Phương pháp giải :

+) Kẻ đường cao $AH$

+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông thích hợp  và định lý Py-ta-go để tính cạnh.

Lời giải chi tiết :

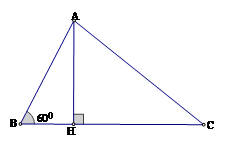Kẻ đường cao \(AH\).

Xét tam giác vuông \(ABH\), ta có: \(BH = AB.\cos B = AB.\cos {60^0} = 16.\dfrac{1}{2} = 8\)\(AH = AB.\sin B = AB.\sin {60^0} = 16.\dfrac{{\sqrt 3 }}{2} = 8\sqrt 3 \).

 Áp dụng định lý Pythago vào tam giác vuông \(AHC\) ta có:

\(H{C^2} = A{C^2} - A{H^2} = {14^2} - {\left( {8\sqrt 3 } \right)^2} = 196 - 192 = 4\). Suy ra \(HC = 2\). Vậy \(BC = CH + HB = 2 + 8 = 10\).

Câu 7 :

Cho tam giác $ABC$ có $\widehat B = {60^0},\widehat C = {50^0},AC = 3,5cm.$ Diện tích tam giác $ABC$ gần nhất với giá trị nào dưới đây?

  • A

    $4$

  • B

    $5$

  • C

    $7$

  • D

    $8$

Đáp án : B

Phương pháp giải :

+) Kẻ đường cao $AD$

+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông thích hợp  và định lý Py-ta-go để tính cạnh.

+) Sử dụng công thức tính diện tích tam giác.

Lời giải chi tiết :

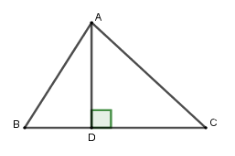Kẻ đường cao \(AD\).

Xét tam giác vuông \(ACD\), có $AD = AC.\sin C = 3,5.\sin 50^\circ  \approx 2,68\,cm$; $CD = AC.\cos C = 3,5.\cos 50^\circ  \approx 2,25\,\,cm$

Xét tam giác vuông \(ABD\), có $BD = AD.\cot B \approx 2,68.\cot 60^\circ  \approx 1,55\,\,cm$

Suy ra $BC = BD + CD = 3,8$

Do đó ${S_{ABC}} = \dfrac{{AD.BC}}{2} \approx 5,09$$c{m^2}$.

Câu 8 :

Cho tứ giác $ABCD$ có $\widehat A = \widehat D = {90^0},\widehat C = {40^0},AB = 4cm,AD = 3cm.$ Tính diện tích tứ giác $ABCD.$ (làm tròn đến chữ số thập phân thứ hai)

  • A

    $17,36\,\,c{m^2}$

  • B

    $17,4\,\,c{m^2}$

  • C

    $17,58\,\,c{m^2}$

  • D

    $17,54\,\,c{m^2}$

Đáp án : A

Phương pháp giải :

+) Kẻ đường cao $BE$

+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông thích hợp để tính $EC$.

+) Sử dụng công thức tính diện tích hình thang

Lời giải chi tiết :

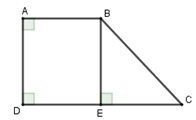Vì $\widehat A = \widehat D = {90^0} \Rightarrow AD{\rm{//}}BC$ hay $ABCD$ là hình thang vuông tại $A,D$

Kẻ $BE \bot DC$ tại $E$.

Tứ giác $ABED$ có ba góc vuông $\widehat A = \widehat D = \widehat E = 90^\circ $ nên $ABED$ là hình chữ nhật

Suy ra $DE = AB = 4\,\,cm;BE = AD = 3\,cm$

Xét tam giác $BEC$ vuông tại $E$ có $EC = BE.\cot 40^\circ=3.\cot40^0 $ $\Rightarrow DC = DE + EC =4+3.\cot40^0$

Do đó ${S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AD}}{2}$\(=\dfrac{(4+4+3.\cot40^0).3}{2}\)

$\approx 17,36\,\,c{m^2}$.

Câu 9 :

Cho tam giác \(DEF\) có \(DE = 7cm;\angle D = {40^0};\angle F = {58^0}\). Kẻ đường cao \(EI\) của tam giác đó.

Hãy tính:  (Kết quả làm tròn đến chữ số thập phân thứ 1)

Câu 9.1

Đường cao \(EI\)

  • A.
    \(EI = 4,5cm\)
  • B.
    \(EI = 5,4cm\)
  • C.
    \(EI = 5,9cm\)
  • D.
    \(EI = 5,6cm\)

Đáp án : A

Phương pháp giải :

Sử dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông.

Lời giải chi tiết :

Xét \(\Delta DEI\) vuông tại \(I\)  ta có:  \(EI = ED.\sin D = 7.\sin {40^0}\)\( \approx 4,5\,\,cm.\)

Câu 9.2

Cạnh \(EF\)

  • A.
    \(EF = 4,5cm\)
  • B.
    \(EF = 5,3cm\)
  • C.
    \(EF = 5,9cm\)
  • D.
    \(EF = 6,2cm\)

Đáp án : B

Phương pháp giải :

Sử dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông.

Lời giải chi tiết :

Xét \(\Delta EIF\) vuông tại \(I\)  ta có: 

\(EI = EF.\sin F \Leftrightarrow EF = \dfrac{{EI}}{{\sin F}} \approx \dfrac{{4,5}}{{\sin {{58}^0}}} \approx 5,3\,cm.\)

Câu 10 :

Cho tam giác $ABC$ có $BC = 11cm,\widehat {ABC} = 40^\circ $ và $\widehat {ACB} = {30^0}.$ Gọi $N$ là chân đường vuông góc hạ từ $A$ xuống cạnh $BC$. 

Câu 10.1

Độ dài $AN$ gần nhất với giá trị nào dưới đây ?

  • A.

    $5$

  • B.

    $4$

  • C.

    $6$

  • D.

    $7$

Đáp án : B

Lời giải chi tiết :

Đặt $BN = x\,\left( {0 < x < 11} \right)$$ \Rightarrow NC = 11 - x$

Xét tam giác $ABN$ vuông tại $N$ có $AN = BN.\tan B = x.\tan 40^\circ $

Xét tam giác $ACN$ vuông tại $N$ có $AN = CN.\tan C = \left( {11 - x} \right).\tan 30^\circ $

Nên $x\tan 40^\circ  = \left( {11 - x} \right)\tan 30^\circ $

$\Rightarrow x \approx 4,48 $ (thoả mãn)

Khi đó $AN = BN.\tan B = 4,48.\tan 40^\circ  \approx 3,76(cm).$

Câu 10.2

Độ dài $AC$ gần nhất với giá trị nào dưới đây ?

  • A.

    $7$

  • B.

    $6$

  • C.

     $5$

  • D.

    $4$

Đáp án : A

Lời giải chi tiết :

Theo câu trước ta có $AN \approx 3,76$;

Xét tam giác $ACN$ vuông tại $N$ có $\sin C = \dfrac{{AN}}{{AC}} \Rightarrow AC = \dfrac{{AN}}{{\sin C}} = 7,52$

Câu 10.3

Diện tích tam giác $ABC$ gần với giá trị nào dưới đây ?

  • A.

    $27$

  • B.

    $23$

  • C.

    $22$

  • D.

    $21$

Đáp án : D

Phương pháp giải :

+) Sử dụng công thức diện tích tam giác $S = \dfrac{{ah}}{2}$ với $h$ là chiều cao ứng với cạnh đáy $a$.

Lời giải chi tiết :

Theo kết quả các câu trước ta có $AN \approx 3,76$ nên ${S_{ABC}} = \dfrac{{AN.BC}}{2} = 20,68\,c{m^2}$.

Câu 11 :

Cho tam giác \(ABC\) cân tại \(A,\,\,\angle B = {65^0},\)  đường cao \(CH = 3,6\).  Hãy giải tam giác \(ABC\).

  • A
    \(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 5,6\,\,;\,\,BC = 8,52\)
  • B
    \(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 5,6\,\,;\,\,BC = 4,42\)
  • C
    \(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 4,7\,\,;\,\,BC = 4,24\)
  • D
    \(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 4,7\,\,;\,\,BC = 3,97\)

Đáp án : D

Phương pháp giải :

Áp dụng hệ thức về cạnh và góc trong tam giác vuông.

Sử dụng tính chất tam giác cân.

Sử dụng định lý tổng ba góc trong một tam giác.

Lời giải chi tiết :

Vì \(\Delta ABC\) là tam giác cân tại \(A\)\( \Rightarrow \angle C = \angle B = {65^0}\)

Ta có \(\angle A + \angle B + \angle C = {180^0}\)(định lý tổng ba góc trong một tam giác)

\( \Rightarrow \angle A = {180^0} - 2\angle C = {180^0} - {2.65^0} = {50^0}\)

Xét \(\Delta ACH\) vuông tại \(H\) ta có:

\(\sin A = \dfrac{{CH}}{{AC}}\) \( \Leftrightarrow \sin {50^0} = \dfrac{{3,6}}{{AC}}\)\( \Rightarrow AC = \dfrac{{3,6}}{{\sin {{50}^0}}} \approx 4,7\)

Vì \(\Delta ABC\) là tam giác cân tại \(A\)\( \Rightarrow AC = AB \approx 4,7\)

Xét \(\Delta BCH\) vuông tại \(H\) ta có:

\(\sin B = \dfrac{{CH}}{{BC}} \Leftrightarrow \sin {65^0} = \dfrac{{3,6}}{{BC}} \)\(\Rightarrow BC = \dfrac{{3,6}}{{\sin {{65}^0}}} \approx 3,97\)

Câu 12 :

Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\), biết \(HB = 9;HC = 16\). Tính góc \(B\) và góc \(C.\) 

  • A
    \(\angle B = {53^0}8'\,\,\,;\,\,\,\angle C = {36^0}52'\)
  • B
    \(\angle B = {36^0}52'\,\,\,;\,\,\,\angle C = {53^0}8'\)
  • C
    \(\angle B = {48^0}35'\,\,\,;\,\,\,\angle C = {41^0}25'\)
  • D
    \(\angle B = {41^0}25'\,\,\,;\,\,\,\angle C = {48^0}35'\)

Đáp án : A

Phương pháp giải :

Áp dụng hệ thức về cạnh và góc trong tam giác vuông

Từ tỉ số lượng giác suy ra số đo góc

Sử dụng hệ thức lượng trong tam giác vuông: \(A{B^2} = BH.BC\); \(A{C^2} = CH.BC\)

Lời giải chi tiết :

Ta có: \(BC = BH + CH = 9 + 16 = 25\)

Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:

\(A{B^2} = BH.BC\)\( \Leftrightarrow A{B^2} = 9.25 \Rightarrow AB = 15\)

\(A{C^2} = CH.BC\)\( \Leftrightarrow A{C^2} = 16.25 \Rightarrow AC = 20\)

Xét \(\Delta ABC\) vuông tại \(A\) ta có

\(\sin B = \dfrac{{AC}}{{BC}} = \dfrac{{20}}{{25}} = \dfrac{4}{5} \Rightarrow \angle B \approx {53^0}8'\)

\(\sin C = \dfrac{{AB}}{{BC}} = \dfrac{{15}}{{25}} = \dfrac{3}{5} \Rightarrow \angle C \approx {36^0}52'\)

Câu 13 :

Một tam giác cân có đường cao ứng với đáy đúng bằng độ dài đáy. Tính các góc của tam giác đó.

  • A
    \(\angle A = {45^0}\,\,;\,\,\,\angle B = \angle C = {67^0}30'\)
  • B
    \(\angle A = {30^0}\,\,;\,\,\,\angle B = \angle C = {75^0}\)
  • C
    \(\angle A = {48^0}6'\,\,;\,\,\,\angle B = \angle C = {65^0}57'\)
  • D
    \(\angle A = {53^0}8'\,\,;\,\,\,\angle B = \angle C = {63^0}26'\)

Đáp án : D

Phương pháp giải :

Áp dụng hệ thức về cạnh và góc trong tam giác vuông.

Tính chất tam giác cân.

Sử dụng định lý tổng ba góc trong một tam giác.

Lời giải chi tiết :

Giả sử \(BC = AH = a.\) 

Vì \(\Delta ABC\) là tam giác cân nên \(AH\) là đường cao đồng thời là đường trung tuyến

\( \Rightarrow H\) là trung điểm \(BC\) \( \Rightarrow HB = HC = \dfrac{{BC}}{2} = \dfrac{a}{2}\)

Xét \(\Delta ABH\) vuông tại \(H\) ta có:  \(tan\angle B = \dfrac{{AH}}{{BH}} = \dfrac{a}{{\dfrac{a}{2}}} = 2\) \( \Rightarrow \angle B \approx {63^0}26'\)

Vì \(\Delta ABC\) là tam giác cân\( \Rightarrow \angle C = \angle B \approx {63^0}26'\)

Ta có \(\angle A + \angle B + \angle C = {180^0}\) (định lý tổng ba góc trong một tam giác)

\( \Rightarrow \angle A = {180^0} - 2\angle C \approx {180^0} - {2.63^0}26' \approx {53^0}8'\)

Câu 14 :

Cho tam giác \(ABC\) vuông cân tại \(A\left( {AB = AC = a} \right)\) . Phân giác của góc \(B\) cắt \(AC\) tại \(D\).

Tính \(DA;DC\) theo \(a\).

  • A
    \(AD = a.\cos 22,{5^0}\,\,;\,\,DC = a - a.\cos 22,{5^0}\)
  • B
    \(AD = a.\sin 22,{5^0}\,\,;\,\,DC = a - a.\sin 22,{5^0}\)
  • C
    \(AD = a.\tan 22,{5^0}\,\,;\,\,DC = a - a.\tan 22,{5^0}\)
  • D
    \(AD = a.\cot 22,{5^0}\,\,;\,\,DC = a - a.cot22,{5^0}\)

Đáp án : C

Phương pháp giải :

Áp dụng hệ thức về cạnh và góc trong tam giác vuông

Sử dụng tính chất tam giác vuông cân và tia phân giác.

Lời giải chi tiết :

Vì tam giác \(ABC\) vuông cân tại \( \Rightarrow \angle B = \angle C = {45^0}\)

Vì \(BD\) là tia phân giác \(B\)

\( \Rightarrow \angle ABD = \angle DBC = \dfrac{1}{2}\angle B = \dfrac{{{{45}^0}}}{2} = 22,{5^0}\)

Xét \(\Delta ABD\) vuông tại \(A\) ta có 

\(AD = AB.\tan \angle ABD = a.\tan 22,{5^0}\)

Ta có: \(AD + DC = AC\)\( \Rightarrow DC = AC - AD = a - a\tan 22,{5^0}\)

Câu 15 :

Cho hình thang \(ABCD\) vuông tại \(A\) và \(D;\)\(\angle C = {50^0}\). Biết \(AB = 2;AD = 1,2\). Tính diện tích hình thang \(ABCD.\)

  • A

    \({S_{ABCD}} = 2\,\,\,\left( {đvdt} \right)\)

  • B

    \({S_{ABCD}} = 3\,\,\,\left( {đvdt} \right)\)

  • C

    \({S_{ABCD}} = 4\,\,\,\left( {đvdt} \right)\)

  • D

    \({S_{ABCD}} = \dfrac{5}{2}\,\,\,\left( {đvdt} \right)\)

Đáp án : B

Phương pháp giải :

Áp dụng hệ thức về cạnh và góc trong tam giác vuông.

Sử dụng tính chất hình chữ nhật.

Công thức tính diện tích hình thang vuông: \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AD}}{2}.\)

Lời giải chi tiết :

Kẻ \(BE \bot DC,\,\,\,E \in CD.\)

Xét tứ giác \(ABED\) có \(\angle A = \angle D = \angle E = {90^0}\)

\( \Rightarrow ABED\) là hình chữ nhật \( \Rightarrow \left\{ \begin{array}{l}AB = ED = 2\\AD = BE = 1,2\end{array} \right.\)

Xét \(\Delta BCE\) vuông tại \(E\) ta có: \(EC = BE.cot\angle C = 1,2.cot{50^0}\)

\( \Rightarrow DC = DE + EC = 2 + 1,2.\cot {50^0}\) 

\( \Rightarrow {S_{ABCD}} = \dfrac{{\left( {AB + CD} \right)AD}}{2}\)\( = \dfrac{{\left( {2 + 2 + 1,2.\cot {{50}^0}} \right).1,2}}{2} \approx 3\,\,\,\,\left( {đvdt} \right).\)

Câu 16 :

Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(AB = 3cm,\,\,AC = 4cm.\) Tính độ dài đường cao \(AH,\) tính \(\cos \angle ACB\).

  • A

    \(AH = 2,8cm\,\,\,;\,\,\,\cos \angle ACB = \dfrac{3}{5}\)

  • B

    \(AH = 2,4cm\,\,\,;\,\,\,\cos \angle ACB = \dfrac{4}{5}\)

  • C

    \(AH = 2,5cm\,\,\,;\,\,\,\cos \angle ACB = \dfrac{3}{4}\)

  • D

    \(AH = 1,8cm\,\,\,;\,\,\,\cos \angle ACB = \dfrac{2}{3}\)

Đáp án : B

Phương pháp giải :

Sử dụng hệ thức lượng trong tam giác vuông và công thức tỉ số lượng giác để làm bài toán.

Lời giải chi tiết :

Áp dụng định lý Pitago trong \(\Delta ABC\) vuông tại \(A\) ta có: \(B{C^2} = A{C^2} + A{B^2} = {3^2} + {4^2} = {5^2} \Rightarrow BC = 5\,\,cm.\)

Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:

\(AH.BC = AB.AC \Leftrightarrow AH = \dfrac{{AB.AC}}{{BC}} \)\(= \dfrac{{3.4}}{5} = 2,4cm.\) 

Ta có: \(\cos \angle ACB = \dfrac{{AC}}{{BC}} = \dfrac{4}{5}.\)

Câu 17 :

Cho tam giác \(ABC\) vuông tại \(A\); \(BC = a\) không đổi, \(\angle C = \alpha \,\,\,\left( {{0^0} < \alpha  < {{90}^0}} \right)\)

Câu 17.1

Lập công thức để tính diện tích tam giác ABC theo \(a\) và \(\alpha\) .

  • A.

    \(\dfrac{1}{2}{a^2}\sin \alpha .\cos \alpha \)

  • B.
    \({a^2}\sin \alpha .\cos \alpha \)
  • C.
    \(2{a^2}\sin \alpha .\cos \alpha \)
  • D.
    \(3{a^2}\sin \alpha .\cos \alpha \)

Đáp án : A

Phương pháp giải :

Áp dụng hệ thức về cạnh và góc trong tam giác vuông.

Sử dụng công thức tính diện tích tam giác \({S_{ABC}} = \dfrac{1}{2}AB.AC.\)

Lời giải chi tiết :

Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\left\{ \begin{array}{l}AB = BC.\sin \alpha  = a.\sin \alpha \\AC = BC.cos\alpha  = a.cos\alpha \end{array} \right.\)

\({S_{ABC}} = \dfrac{1}{2}.AB.AC = \dfrac{1}{2}a.\sin \alpha .a.cos\alpha  \)\(= \dfrac{1}{2}{a^2}.\sin \alpha .cos\alpha \)

Câu 17.2

Tìm góc  để diện tích tam giác ABC là lớn nhất. Tính giá trị lớn nhất ấy.

  • A.

    \(\alpha  = {45^0}\,\,;\,\,\max {S_{\Delta ABC}} = \dfrac{1}{2}{a^2}\)

  • B.

    \(\alpha  = {30^0}\,\,;\,\,\max {S_{\Delta ABC}} = \dfrac{{\sqrt 3 }}{4}{a^2}\)

  • C.

    \(\alpha  = {60^0}\,\,;\,\,\max {S_{\Delta ABC}} = \dfrac{{\sqrt 3 }}{4}{a^2}\)

  • D.

    \(\alpha  = {45^0}\,\,;\,\,\max {S_{\Delta ABC}} = \dfrac{1}{4}{a^2}\)

Đáp án : D

Phương pháp giải :

Sử dụng định lý Pytago.

Áp dụng bất đẳng thức Cô-si

Lời giải chi tiết :

Áp dụng bất đẳng thức Cô-si ta có:

\({S_{ABC}} = \dfrac{1}{2}.AB.AC \le \dfrac{1}{2}.\dfrac{{\left( {A{B^2} + A{C^2}} \right)}}{2}\)\( = \dfrac{1}{4}.\left( {A{B^2} + A{C^2}} \right)\)

Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) ta có: \(A{B^2} + A{C^2} = B{C^2}\)

\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}.AB.AC \le \dfrac{1}{4}.\left( {A{B^2} + A{C^2}} \right) = \dfrac{1}{4}B{C^2} = \dfrac{1}{4}{a^2}\)

Dấu “=” xảy ra \( \Leftrightarrow AC = AB\)\( \Leftrightarrow \Delta ABC\) vuông cân  \( \Rightarrow \angle B = \angle C = {45^0}\) hay \(\alpha  = {45^0}\).

Vậy \({S_{ABCmax}} = \dfrac{1}{4}{a^2}\) khi \(\alpha  = {45^0}.\)

Bài liên quan
close

Tiện ích | Blog

Nội dung từ Loigiaihay.Com