Trắc nghiệm Bài 1,2: Hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2 Toán 9Đề bài
Câu 1 :
Cho hàm số y=ax2 với a≠0. Kết luận nào sau đây là đúng?
Câu 2 :
Kết luận nào sau đây là sai khi nói về đồ thị của hàm số y=ax2 với a≠0.
Câu 3 :
Giá trị của hàm số y=f(x)=−7x2 tại x0=−2 là
Câu 4 :
Cho hàm số y=f(x)=(−2m+1)x2. Tìm giá trị của m để đồ thị đi qua điểm A(−2;4).
Câu 5 :
Cho hàm số y=f(x)=−2x2 . Tổng các giá trị của a thỏa mãn f(a)=−8+4√3 là
Câu 6 :
Cho hàm số y=(5m+2)x2 với m≠−25. Tìm m để hàm số nghịch biến với mọi x>0.
Câu 7 :
Cho hàm số y=(4−3m)x2 với m≠43. Tìm m để hàm số đồng biến với mọi x>0
Câu 8 :
Trong các điểm A(1;2);B(−1;−1);C(10;−200);D(√10;−10) có bao nhiêu điểm thuộc đồ thị hàm số (P):y=−x2
Câu 9 :
Cho hàm số y=f(x)=3x2. Tìm b biết f(b)≥6b+9.
Câu 10 :
Cho hàm số y=(2m+2)x2. Tìm m để đồ thị hàm số đi qua điểm A(x;y) với (x;y) là nghiệm của hệ phương trình {x−y=12x−y=3
Câu 11 :
Cho hàm số y=(−m2+4m−5)x2 . Kết luận nào sau đây là đúng
Câu 12 :
Hình vẽ dưới đây là của đồ thị hàm số nào? 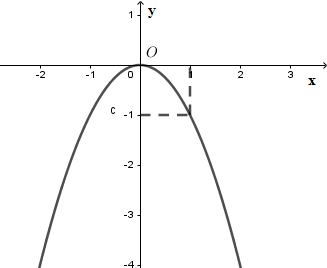
Câu 13 :
Cho hàm số y=√3x2có đồ thị là (P). Có bao nhiêu điểm trên (P) có tung độ gấp đôi hoành độ.
Câu 14 :
Cho (P):y=12x2;(d):y=x−12. Tìm toạ độ giao điểm của (P) và (d).
Câu 15 :
Cho parabol y=14x2. Xác định m để điểm A(√2;m) nằm trên parabol.
Câu 16 :
Cho parabol(P):y=2x2 và đường thẳng (d):y=x+1. Số giao điểm của đường thẳng d và parabol (P) là:
Câu 17 :
Cho parabol (P):y=(m−1)x2 và đường thẳng (d):y=3−2x. Tìm m để đường thẳng d cắt (P) tại điểm có tung độ y=5.
Câu 18 :
Cho parabol (P):y=(1−2m2)x2 và đường thẳng (d):y=2x+2. Biết đường thẳng d cắt (P) tại một điểm có tung độ y=4. Tìm hoành độ giao điểm còn lại của d và parabol (P).
Câu 19 :
Cho đồ thị hàm số y=2x2(P) như hình vẽ. Dựa vào đồ thị, tìm m để phương trình 2x2−m−5=0 có hai nghiệm phân biệt. 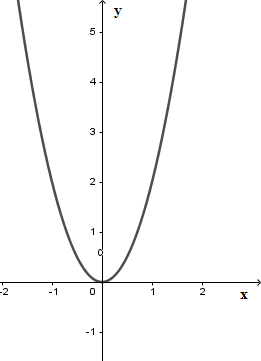
Câu 20 :
Lực F của gió thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương vận tốc v của gió tức là: F=av2 với a là hằng số. Biết rằng khi vận tốc của gió là 2,5m/s thì lực tác động lên cánh buồm là 150N. Biết thuyền buồm vẫn có thể đi được nếu vận tốc gió lớn nhất là 90km/h. Tính áp lực lớn nhất mà cánh buồm có thể chịu được.
Câu 21 :
Giá trị nhỏ nhất của hàm số y=−2x2 khi x∈[−3;5] là:
Câu 22 :
Tìm tất cả các giá trị của tham số m để đường thẳng y=x+3−m cắt parabol y=x2 tại hai điểm phân biệt.
Câu 23 :
Cổng vào một ngôi biệt thự có hình dạng là một parabol được biểu diễn bởi đồ thị hàm số y=−x2. Biết khoảng cách giữa hai chân cổng là 4m. Một chiếc ô tô tải có thùng xe là một hình hộp chữ nhật có chiều rộng là 2,4m. Hỏi chiều cao lớn nhất có thể của ô tô là bao nhiêu để ô tô có thể đi qua cổng?
Câu 24 :
Cho parabol y=−x2. Vẽ đường thẳng song song với trục hoành cắt trục tung tại điểm −5 và cắt parabol tại M và N. Diện tích tam giác OMN là
Câu 25 :
Cho parabol (P):y=f(x)=x2 . Đường thẳng d:y=m cắt (P) tại hai điểm A và B sao cho tam giác OAB đều.
Lời giải và đáp án
Câu 1 :
Cho hàm số y=ax2 với a≠0. Kết luận nào sau đây là đúng?
Đáp án : C Lời giải chi tiết :
Cho hàm số y=ax2(a≠0). a) Nếu a>0 thì hàm số nghịch biến khi x<0 và đồng biến khi x>0. b) Nếu a<0 thì hàm số đồng biến khi x<0 và nghịch biến khi x>0.
Câu 2 :
Kết luận nào sau đây là sai khi nói về đồ thị của hàm số y=ax2 với a≠0.
Đáp án : B Lời giải chi tiết :
Đồ thị của hàm số y=ax2(a≠0) là một parabol đi qua gốc tọa độ O, nhận Oy là trục đối xứng (O là đỉnh của parabol). - Nếu a>0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị. - Nếu a<0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Câu 3 :
Giá trị của hàm số y=f(x)=−7x2 tại x0=−2 là
Đáp án : D Phương pháp giải :
Giá trị của hàm số y=ax2(a≠0) tại điểm x=x0 là y0=axo2. Lời giải chi tiết :
Thay x0=−2 vào hàm số y=f(x)=−7x2 ta được f(−2)=−7.(−2)2=−28
Câu 4 :
Cho hàm số y=f(x)=(−2m+1)x2. Tìm giá trị của m để đồ thị đi qua điểm A(−2;4).
Đáp án : A Phương pháp giải :
Đồ thị hàm số y=ax2(a≠0) đi qua điểm A(x0;y0) khi y0=axo2. Lời giải chi tiết :
Thay tọa độ điểm A(−2;4) vào hàm số y=f(x)=(−2m+1)x2 ta được (−2m+1).(−2)2=4−2m+1=1m=0 Vậy m=0 là giá trị cần tìm.
Câu 5 :
Cho hàm số y=f(x)=−2x2 . Tổng các giá trị của a thỏa mãn f(a)=−8+4√3 là
Đáp án : B Phương pháp giải :
Giá trị của hàm số y=ax2(a≠0) tại điểm x=x0 là y0=axo2. Sử dụng hằng đẳng thức bình phương của một hiệu để tính. Lời giải chi tiết :
Ta có f(a)=−8+4√3 hay −2a2=−8+4√3 a2=4−2√3 a2=3−2√3+1 a2=(√3−1)2 Suy ra a=√3−1 hoặc a=1−√3 Vậy tổng các giá trị của a là (√3−1)+(1−√3)=0
Câu 6 :
Cho hàm số y=(5m+2)x2 với m≠−25. Tìm m để hàm số nghịch biến với mọi x>0.
Đáp án : A Phương pháp giải :
Xét hàm số y=ax2(a≠0). Ta có: +) Nếu a>0 thì hàm số nghịch biến khi x<0 và đồng biến khi x>0. +) Nếu a<0 thì hàm số đồng biến khi x<0 và nghịch biến khi x>0. Lời giải chi tiết :
Để hàm số nghịch biến với mọi x>0 thì a<0 nên 5m+2<0⇔m<−25. Vậy m<−25 thỏa mãn điều kiện đề bài.
Câu 7 :
Cho hàm số y=(4−3m)x2 với m≠43. Tìm m để hàm số đồng biến với mọi x>0
Đáp án : C Phương pháp giải :
Xét hàm số y=ax2(a≠0). Ta có: +) Nếu a>0 thì hàm số nghịch biến khi x<0 và đồng biến khi x>0. +) Nếu a<0 thì hàm số đồng biến khi x<0 và nghịch biến khi x>0. Lời giải chi tiết :
Để hàm số đồng biến với mọi x>0 thì a>0 nên 4−3m>0⇔4>3m⇔3m<4⇔m<43. Vậy m<43 thỏa mãn điều kiện đề bài
Câu 8 :
Trong các điểm A(1;2);B(−1;−1);C(10;−200);D(√10;−10) có bao nhiêu điểm thuộc đồ thị hàm số (P):y=−x2
Đáp án : D Phương pháp giải :
Điểm M(x0;y0) thuộc đồ thị hàm số y=ax2(a≠0) khi y0=ax20 Lời giải chi tiết :
+) Thay tọa độ điểm A(1;2) vào hàm số y=−x2 ta được 2=−12( vô lý) nên A∉(P) +) Thay tọa độ điểm C(10;−200) vào hàm số y=−x2 ta được −200=−(10)2 hay −200=−100( vô lý) nên loại C∉(P) +) Thay tọa độ điểm D(√10;−10) vào hàm số y=−x2 ta được −10=−(√10)2 hay −10=−10( luôn đúng) nên D∈(P) +) Thay tọa độ điểm B(−1;−1) vào hàm số y=−x2 ta được −1=−(−1)2⇔−1=−1 (luôn đúng) B∈(P).
Câu 9 :
Cho hàm số y=f(x)=3x2. Tìm b biết f(b)≥6b+9.
Đáp án : C Phương pháp giải :
Sử dụng : Giá trị của hàm số y=ax2(a≠0) tại điểm x=x0 là y0=axo2 Sau đó giải bất bất phương trình thu được Lời giải chi tiết :
Ta có f(b)≥6b+9 ⇔3b2≥6b+9⇔b2−2b−3≥0⇔(b+1)(b−3)≥0 TH1:{b+1≥0b−3≥0⇔{b≥−1b≥3⇒b≥3TH2:{b+1≤0b−3≤0⇔{b≤−1b≤3⇒b≤−1 Vậy [b≤−1b≥3 là giá trị cần tìm.
Câu 10 :
Cho hàm số y=(2m+2)x2. Tìm m để đồ thị hàm số đi qua điểm A(x;y) với (x;y) là nghiệm của hệ phương trình {x−y=12x−y=3
Đáp án : D Phương pháp giải :
Bước 1: Giải hệ phương trình cho trước bằng phương pháp thế hoặc cộng đại số ta tìm được (x;y) Bước 2: Đồ thị hàm số y=ax2(a≠0) đi qua điểm A(x0;y0) khi y0=axo2 từ đó tìm được m Lời giải chi tiết :
Ta có: {x−y=1(1)2x−y=3(2) Từ phương trình (1) suy ra x=y+1. Thay vào phương trình (2), ta được: 2(y+1)−y=3 suy ra y=1 Thay vào x=y+1 ta được x=1+1=2. Ta được điểm A(2;1) thuộc đồ thị hàm số. Thay x=2;y=1 vào hàm số y=(2m+2)x2 ta được 1=(2m+2).222m+2=142m=−74m=−78 Vậy m=−78 là giá trị cần tìm.
Câu 11 :
Cho hàm số y=(−m2+4m−5)x2 . Kết luận nào sau đây là đúng
Đáp án : B Phương pháp giải :
Bước 1: Đánh giá hệ số a của x2 Bước 2: Ta sử dụng các kiến thức sau để kết luận * Xét hàm số y=ax2(a≠0). Ta có: - Nếu a>0 thì hàm số nghịch biến khi x<0 và đồng biến khi x>0. - Nếu a<0 thì hàm số đồng biến khi x<0 và nghịch biến khi x>0. * Đồ thị của hàm số y=ax2(a≠0) là một đường cong (parabol) đi qua gốc tọa độ O. - Nếu a>0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị. - Nếu a<0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị. Lời giải chi tiết :
Ta thấy hàm số y=(−m2+4m−5)x2 có a=−m2+4m−5=−(m2−4m+4)−1=−(m−2)2−1 Vì (m−2)2≥0 với mọi m nên −(m−2)2≤0 với mọi m Suy ra −(m−2)2−1≤0−1⇒−(m−2)2−1≤−1<0 với mọi m Hay a<0 với mọi m Nên hàm số đồng biến khi x<0 và nghịch biến khi x>0. Suy ra C,D sai. Và đồ thị hàm số nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị. Suy ra A sai.
Câu 12 :
Hình vẽ dưới đây là của đồ thị hàm số nào? 
Đáp án : A Phương pháp giải :
Ta sử dụng các kiến thức sau: * Đồ thị của hàm số y=ax2(a≠0) là một đường cong (parabol) đi qua gốc tọa độ O. - Nếu a>0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị. - Nếu a<0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị. * Đồ thị hàm số y=ax2(a≠0) đi qua điểm A(x0;y0) khi y0=axo2 Lời giải chi tiết :
Từ hình vẽ suy ra a<0 nên loại B,C Vì đồ thị đi qua điểm có tọa độ (1;−1) nên loại D.
Câu 13 :
Cho hàm số y=√3x2có đồ thị là (P). Có bao nhiêu điểm trên (P) có tung độ gấp đôi hoành độ.
Đáp án : D Phương pháp giải :
Bước 1: Gọi điểm M(x;y) thỏa mãn điều kiện đề bài. Biểu diễn x theo y hoặc y theo x . Bước 2: Thay tọa độ điểm M vào hàm số ta tìm được x từ đó suy ra M . Lời giải chi tiết :
Gọi điểm M(x;y) là điểm cần tìm. Vì M có tung độ gấp đôi hoành độ nên M(x;2x). Thay tọa độ điểm M vào hàm số ta được 2x=√3x2√3x2−2x=0x.(√3x−2)=0 Suy ra x=0 hoặc √3x−2=0 hay x=0 hoặc x=2√33 + Với x=0 thì y=0 là điểm O(0;0). + Với x=2√33 thì y=22√33=4√33 Vậy có hai điểm thỏa mãn điều kiện là O(0;0),M(2√33;4√33).
Câu 14 :
Cho (P):y=12x2;(d):y=x−12. Tìm toạ độ giao điểm của (P) và (d).
Đáp án : A Phương pháp giải :
Cho parabol (P):y=ax2(a≠0) và đường thẳng d:y=mx+n. Để tìm tọa độ giao điểm (nếu có) của (d) và (P), ta làm như sau: Bước 1. Xét phương trình hoành độ giao điểm của (d) và (P): ax2=mx+n Bước 2. Giải phương trình (*) ta tìm được nghiệm (nếu có). Từ đó ta tìm được tọa độ giao điểm của (d) và (P) Lời giải chi tiết :
Xét phương trình hoành độ giao điểm của parabol (P) và đường thẳng d 12x2=x−12x2−2x+1=0(x−1)2=0x−1=0x=1 Thay x=1 vào hàm số y=12x2 ta được y=12.12=12 Nên tọa độ giao điểm cần tìm là (1;12).
Câu 15 :
Cho parabol y=14x2. Xác định m để điểm A(√2;m) nằm trên parabol.
Đáp án : A Phương pháp giải :
Đồ thị hàm số y=ax2(a≠0) đi qua điểm A(x0;y0) khi y0=axo2 từ đó tìm được m Lời giải chi tiết :
Thay x=√2;y=m vào hàm số y=14x2 ta được m=14.(√2)2=12. Vậy m=12.
Câu 16 :
Cho parabol(P):y=2x2 và đường thẳng (d):y=x+1. Số giao điểm của đường thẳng d và parabol (P) là:
Đáp án : D Phương pháp giải :
Cho parabol (P):y=ax2(a≠0) và đường thẳng d:y=mx+n. Để tìm tọa độ giao điểm (nếu có) của (d) và (P), ta làm như sau: Bước 1. Xét phương trình hoành độ giao điểm của (d) và (P): ax2=mx+n Bước 2. Giải phương trình (*) ta tìm được nghiệm (nếu có). Từ đó suy ra số giao điểm của parabol và đường thẳng. Lời giải chi tiết :
Xét phương trình hoành độ giao điểm của parabol (P) và đường thẳng d 2x2=x+12x2−x−1=02x2−2x+x−1=02x(x−1)+(x−1)=0(2x+1)(x−1)=0 Suy ra x=−12 hoặc x=1 Vậy có hai giao điểm của đường thẳng d và parabol (P).
Câu 17 :
Cho parabol (P):y=(m−1)x2 và đường thẳng (d):y=3−2x. Tìm m để đường thẳng d cắt (P) tại điểm có tung độ y=5.
Đáp án : C Phương pháp giải :
Bước 1: Thay tung độ giao điểm vào phương trình đường thẳng d để tìm hoành độ giao điểm. Bước 2: Thay tọa độ giao điểm vào phương trình parabol ta tìm được m. Lời giải chi tiết :
Thay y=5 vào phương trình đường thẳng d ta được 5=3−2x suy ra x=−1 Nên tọa độ giao điểm của đường thẳng d và parabol (P) là (−1;5) Thay x=−1;y=5 vào hàm số y=(m−1)x2 ta được (m−1).(−1)2=5m−1=5m=6 Vậy m=6 là giá trị cần tìm.
Câu 18 :
Cho parabol (P):y=(1−2m2)x2 và đường thẳng (d):y=2x+2. Biết đường thẳng d cắt (P) tại một điểm có tung độ y=4. Tìm hoành độ giao điểm còn lại của d và parabol (P).
Đáp án : A Phương pháp giải :
Bước 1: Thay tung độ giao điểm vào phương trình đường thẳng d để tìm hoành độ giao điểm. Bước 2: Thay tọa độ giao điểm vào phương trình parabol ta tìm được m. Bước 3: Giải phương trình hoành độ giao điểm của d và parabol (P) ta tìm được hoành độ giao điểm còn lại. Lời giải chi tiết :
Thay y=4 vào phương trình đường thẳng d ta được 2x+2=4 suy ra x=1 Nên tọa độ giao điểm của đường thẳng d và parabol (P) là (1;4) Thay x=1;y=4 vào hàm số y=(1−2m2)x2 ta được 1−2m2.12=41−2m=8m=−72(P):y=4x2 Xét phương trình hoành độ giao điểm của d và (P) : 4x2=2x+22x2−x−1=0(2x+1)(x−1)=0 Suy ra x=−12 hoặc x=1. Vậy hoành độ giao điểm còn lại là x=−12.
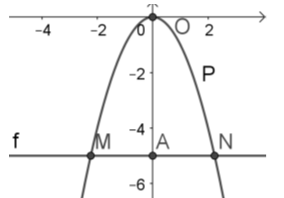
Câu 19 :
Cho đồ thị hàm số y=2x2(P) như hình vẽ. Dựa vào đồ thị, tìm m để phương trình 2x2−m−5=0 có hai nghiệm phân biệt. 
Đáp án : D Phương pháp giải :
Đưa phương trình về dạng ax2=mx+n (*) Gọi parabol (P):y=ax2 và đường thẳng d:y=mx+n Số nghiệm của (*) bằng đúng số giao điểm của . - Nếu (d) không cắt (P) thì (*) vô nghiệm - Nếu (d) tiếp xúc với (P) thì (*) có nghiệm kép - Nếu (d) cắt (P) tại hai điểm phân biệt thì (*) có 2 nghiệm phân biệt . Lời giải chi tiết :
Ta có 2x2−m−5=0 (*) ⇔2x2=m+5 Số nghiệm của phương trình (*) là số giao điểm của parabol (P):y=2x2 và đường thẳng d:y=m+5. Để (*) có hai nghiệm phân biệt thì d cắt (P) tại hai điểm phân biệt. Từ đồ thị hàm số ta thấy Với m+5>0⇔m>−5 thì d cắt (P) tại hai điểm phân biệt hay phương trình (*) có hai nghiệm phân biệt khi m > - 5.
Câu 20 :
Lực F của gió thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương vận tốc v của gió tức là: F = a{v^2} với a là hằng số. Biết rằng khi vận tốc của gió là 2,5m/s thì lực tác động lên cánh buồm là 150N. Biết thuyền buồm vẫn có thể đi được nếu vận tốc gió lớn nhất là 90km/h. Tính áp lực lớn nhất mà cánh buồm có thể chịu được.
Đáp án : A Phương pháp giải :
Tính hằng số a. Khi đó ta có biểu thức F = a{v^2} và có vận tốc gió lớn nhất mà thuyền buồm có thể chịu được thì {F_{\max }} = a.v_{\max }^2. Chú ý đổi đơn vị vận tốc của gió. Lời giải chi tiết :
Theo đề bài ta có: vận tốc của gió là 2,5m/s thì lực tác động lên cánh buồm là 150N Suy ra 150 = a.2,{5^2} hay a = 24\,\,\left( {N{s^2}/{m^2}} \right). Khi đó ta có: F = 24{v^2}. Đổi: {v_{\max }} = 90km/h = \dfrac{{90.1000}}{{3600}} = 25\,\,m/s. Như vậy áp lực lớn nhất mà thuyền buồm có thể chịu được là: {F_{\max }} = 24v_{\max }^2 = {24.25^2} = 15000\,\,N.
Câu 21 :
Giá trị nhỏ nhất của hàm số y = - 2{x^2} khi x \in \left[ { - 3;\,\,5} \right] là:
Đáp án : B Phương pháp giải :
Xét hàm số: y = a{x^2}\,\,\,\left( {a \ne 0} \right) ta có: +) TH1: a > 0 thì hàm số đồng biến khi x > 0 và nghịch biến khi x < 0. +) TH2: a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0. Lời giải chi tiết :
Ta có: y = - 2{x^2} có a = - 2 < 0 \Rightarrow đồ thị hàm số có bề lõm hướng xuống dưới. Và hàm số đồng biến khi x > 0, hàm số nghịch biến khi x < 0. +) Với - 3 \le x < 0 ta có: y\left( { - 3} \right) \le y\left( x \right) < y\left( 0 \right) \Leftrightarrow - 18 \le y\left( x \right) < 0. +) Với 0 \le x \le 5 ta có: y\left( 0 \right) \ge y\left( x \right) \ge y\left( 5 \right) \Leftrightarrow 0 \ge y\left( x \right) \ge - 50 \Rightarrow Với mọi x \in \left[ { - 3;\,\,5} \right] ta có: - 50 \le y\left( x \right) \le 0 Vậy \mathop {Min}\limits_{\left[ { - 3;\,\,5} \right]} y = y\left( { - 5} \right) = - 50.
Câu 22 :
Tìm tất cả các giá trị của tham số m để đường thẳng y = x + 3 - m cắt parabol y = {x^2} tại hai điểm phân biệt.
Đáp án : A Phương pháp giải :
Xét phương trình hoành độ giao điểm (*) của hai đồ thị hàm số. Đường thẳng d cắt parabol \left( P \right) tại hai điểm phân biệt thì phương trình \left( * \right) có hai nghiệm phân biệt hay \Delta > 0. Lời giải chi tiết :
Xét phương trình hoành độ giao điểm của đường thẳng d:\,\,\,y = x + 3 - m và parabol \left( P \right):\,\,y = {x^2} ta có: {x^2} = x + 3 - m {x^2} - x + m - 3 = 0\,\,\,\,\left( * \right) Đường thẳng \left( d \right) cắt \left( P \right) tại hai điểm phân biệt thì phương trình \left( * \right) có hai nghiệm phân biệt hay \Delta > 0 Ta có: \Delta = 1 - 4\left( {m - 3} \right) > 0 hay 1 - 4m + 12 > 0 4m < 13 \\ m < \dfrac{{13}}{4} Vậy m < \dfrac{{13}}{4} thỏa mãn bài toán.
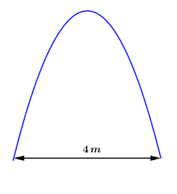
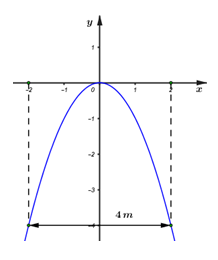
Câu 23 :
Cổng vào một ngôi biệt thự có hình dạng là một parabol được biểu diễn bởi đồ thị hàm số y = - {x^2}. Biết khoảng cách giữa hai chân cổng là 4\,m. Một chiếc ô tô tải có thùng xe là một hình hộp chữ nhật có chiều rộng là 2,4\,m. Hỏi chiều cao lớn nhất có thể của ô tô là bao nhiêu để ô tô có thể đi qua cổng?
Đáp án : B Phương pháp giải :
Sử dụng phương pháp tọa độ hóa tức gắn vào hệ trục tọa độ để tính toán. Lời giải chi tiết :
Ta có đồ thị hàm số của cổng biệt thự như hình vẽ. Khi đó cổng biệt thự có chiều cao h = 4\,m. Chiều rộng của thùng xe ô tô tải là 2,4\,m \Rightarrow {x_0} = \dfrac{1}{2}.2,4 = 1,2m. \Rightarrow Chiều cao lớn nhất của ô tô tải là: {h_0} = 1,{2^2} = 1,44m.
Câu 24 :
Cho parabol y=-{{x}^{2}}. Vẽ đường thẳng song song với trục hoành cắt trục tung tại điểm -5 và cắt parabol tại M và N. Diện tích tam giác OMN là
Đáp án : B Phương pháp giải :
Hoành độ giao điểm hai đồ thị y={{f}_{1}}\left( x \right) và y={{f}_{2}}\left( x \right) là nghiệm của phương trình {{f}_{1}}\left( x \right)-{{f}_{2}}\left( x \right)=0 Công thức tính diện tích tam giác: S=\frac{1}{2}a.h (a là độ dài đáy, h là chiều cao tương ứng) Lời giải chi tiết :
Đường thẳng song song với Ox cắt Oy tại -5 là đường thẳng f:y=-5. Hoành độ giao điểm của \left( P \right) và f là nghiệm của phương trình -{{x}^{2}}=-5 suy ra x=\sqrt{5} hoặc x=-\sqrt{5}. Vậy M(-\sqrt{5};-5);N(\sqrt{5};-5). Ta có: MN=AM+AN=\left| -\sqrt{5} \right|+\left| \sqrt{5} \right|=2\sqrt{5} OA=\left| -5 \right|=5 Vậy {{S}_{OMN}}=\dfrac{1}{2}MN.OA=\dfrac{1}{2}.2\sqrt{5}.5=5\sqrt{5}.
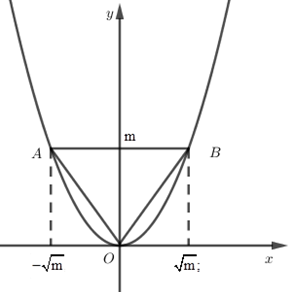
Câu 25 :
Cho parabol \left( P \right):y=f\left( x \right)={{x}^{2}} . Đường thẳng d:y=m cắt \left( P \right) tại hai điểm A và B sao cho tam giác OAB đều.
Đáp án : B Phương pháp giải :
Hoành độ giao điểm hai đồ thị y={{f}_{1}}\left( x \right) và y={{f}_{2}}\left( x \right) là nghiệm của phương trình {{f}_{1}}\left( x \right)-\text{ }{{f}_{2}}\left( x \right)=0 Hai đồ thị hàm số cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình hoành độ giao điểm có 2 nghiệm phân biệt. Lời giải chi tiết :
\left( P \right) cắt d tại 2 điểm phân biệt thì phương trình hoành độ giao điểm {{x}^{2}}-m=0 phải có hai nghiệm phân biệt suy ra m>0. Ta có hoành độ của A và B là nghiệm của phương trình {{x}^{2}}=m suy ra x=\sqrt{m} hoặc x=-\sqrt{m}. Vậy A\left( -\sqrt{m};m \right),B\left( \sqrt{m},m \right). Để OAB là tam giác đều thì OA=OB=AB Mà OA=\sqrt{{{\left( -\sqrt{m} \right)}^{2}}+{{m}^{2}}}, OB=\sqrt{{{\left( \sqrt{m} \right)}^{2}}+{{m}^{2}}}, AB=\left| -\sqrt{m} \right|+\left| \sqrt{m} \right|=2\sqrt{m} Nên ta có \sqrt{{{\left( \sqrt{m} \right)}^{2}}+{{m}^{2}}}=2\sqrt{m} hay m+{{m}^{2}}=4m. Suy ra {{m}^{2}}-3m=0 hay m(m - 3) = 0 Suy ra m=0 hoặc m=3 Kết hợp điều kiện m>0 ta được m=3.
|