Bài tập trắc nghiệm Toán 9

Trắc nghiệm Bài 2: Tỉ số lượng giác của góc nhọn Toán 9

Làm đề thi

Đề bài

Câu 1 :

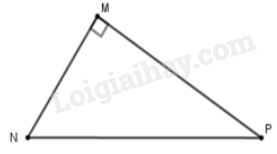
Cho tam giác $MNP$ vuông tại $M$. Khi đó $\cos \widehat {MNP}$ bằng

  • A

    $\dfrac{{MN}}{{NP}}$

  • B

    $\dfrac{{MP}}{{NP}}$

  • C

    $\dfrac{{MN}}{{MP}}$

  • D

    $\dfrac{{MP}}{{MN}}$

Câu 2 :

Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.

  • A

    $\sin \alpha  + \cos \alpha  = 1$

  • B

    ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$

  • C

    ${\sin ^3}\alpha  + {\cos ^3}\alpha  = 1$

  • D

    $\sin \alpha  - cos\alpha  = 1$

Câu 3 :

Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định sai.

  • A

    $\tan \alpha  = \dfrac{{\sin \alpha }}{{\cos \alpha }}\,\,$

  • B

    $\cot \alpha  = \dfrac{{\cos \alpha }}{{\sin \alpha }}\,\,$

  • C

    $\tan \alpha .\cot \alpha  = 1$

  • D

    ${\tan ^2}\alpha  - 1 = {\cos ^2}\alpha $

Câu 4 :

Cho $\alpha $ và $\beta $ là hai góc nhọn bất kỳ thỏa mãn $\alpha  + \beta  = 90^\circ $. Khẳng định nào sau đây là đúng?

  • A

    $\tan \alpha  = \sin \beta $

  • B

    $\tan \alpha  = \cot \beta $

  • C

    $\tan \alpha  = \cos \alpha $

  • D

    $\tan \alpha  = \tan \beta $

Câu 5 :

Cho tam giác $ABC$ vuông tại  $C$ có \(BC = 1,2\,cm,\,\,AC = 0,9\,cm.\) Tính các tỉ số lượng giác $\sin B;\cos B$ .

  • A

    $\sin B = 0,6;\cos B = 0,8$

  • B

    $\sin B = 0,8;\cos B = 0,6$

  • C

    $\sin B = 0,4;\cos B = 0,8$

  • D

    $\sin B = 0,6;\cos B = 0,4$

Câu 6 :

Cho tam giác $ABC$ vuông tại  $A$ có \(BC = 8\,cm,\,\,AC = 6cm.\) Tính tỉ số lượng giác $\tan C$ (làm tròn đến chữ số thập phân thứ $2$ ).

  • A

    $\tan C \approx 0,87$

  • B

    $\tan C \approx 0,86$

  • C

    $\tan C \approx 0,88$

  • D

    $\tan C \approx 0,89$

Câu 7 :

Trong một hộp thưởng có chứa 5 quả bóng xanh, 20 quả bóng trắng, n quả bóng màu cầu vồng, các quả bóng cùng kích thước. Lấy ngẫu nhiên một quả bóng. Biết xác suất lấy được quả bóng màu cầu vồng là \(\frac{3}{4}\). Tính số quả bóng màu cầu vồng.

Đáp án:

Câu 8 :

Cho tam giác $ABC$ vuông tại  $A$, đường cao $AH$ có \(CH = 4\,cm,\,BH = 3\,cm.\) Tính tỉ số lượng giác $\cos C$ (làm tròn đến chữ số thập phân thứ $2$ )

  • A

    $\cos C \approx 0,76$

  • B

    $\cos C \approx 0,77$

  • C

    $\cos C \approx 0,75$

  • D

    $\cos C \approx 0,78$

Câu 9 :

Cho tam giác $ABC$ vuông tại  $A$. Hãy tính $\tan C$ biết rằng \(\cot B = 2\).

  • A

    $\tan C = \dfrac{1}{4}$

  • B

    $\tan C = 4$

  • C

    $\tan C = 2$

  • D

    $\tan C = \dfrac{1}{2}$

Câu 10 :

Cho tam giác $ABC$ vuông tại  $A$ có \(AB = 5\,cm,\,\,\cot C = \dfrac{7}{8}\) . Tính độ dài các đoạn thẳng $AC$ và $BC$ . (làm tròn đến chữ số thập phân thứ $2$ )

  • A

    $AC \approx 4,39 (cm);BC \approx 6,66 (cm)$

  • B

    $AC \approx 4,38(cm);BC \approx 6,64(cm)$

  • C

    $AC \approx 4,38(cm);BC \approx 6,67(cm)$

  • D

    $AC \approx 4,37(cm);BC \approx 6,67(cm)$

Câu 11 :

Cho $\alpha$ là góc nhọn. Tính \(\sin \alpha,\,\cot \alpha \) biết \(\cos \alpha  = \dfrac{2}{5}\).

  • A

    $\sin \alpha  = \dfrac{{\sqrt {21} }}{{25}};\cot \alpha  = \dfrac{{3\sqrt {21} }}{{21}}$

  • B

    $\sin \alpha  = \dfrac{{\sqrt {21} }}{5};\cot \alpha  = \dfrac{5}{{\sqrt {21} }}$

  • C

    $\sin \alpha  = \dfrac{{\sqrt {21} }}{3};\cot \alpha  = \dfrac{3}{{\sqrt {21} }}$

  • D

    $\sin \alpha  = \dfrac{{\sqrt {21} }}{5};\cot \alpha  = \dfrac{2}{{\sqrt {21} }}$

Câu 12 :

Không dùng bảng số và máy tính, hãy so sánh \(\sin 20^\circ \) và \(\sin 70^\circ \)

  • A

    $\sin 20^\circ  < \sin 70^\circ $

  • B

    $\sin 20^\circ  > \sin 70^\circ $

  • C

    $\sin 20^\circ  = \sin 70^\circ $

  • D

    $\sin 20^\circ  \ge \sin 70^\circ $

Câu 13 :

Sắp xếp các tỉ số lượng giác \(\tan 43^\circ ,\,\,\cot 71^\circ ,\,\,\tan 38^\circ ,\,\,\cot 69^\circ 15',\,\tan 28^\circ \) theo thứ tự tăng dần.

  • A

    $\cot 71^\circ  < \cot 69^\circ 15' < \tan 28^\circ  < \tan 38^\circ  < \tan 43^\circ $

  • B

    $\cot 69^\circ 15' < \cot 71^\circ  < \tan 28^\circ  < \tan 38^\circ  < \tan 43^\circ $

  • C

    $\tan 28^\circ  < \tan 38^\circ  < \tan 43^\circ  < \cot 69^\circ 15' < \cot 71^\circ $

  • D

    $\cot 69^\circ 15' < \tan 28^\circ  < \tan 38^\circ  < \tan 43^\circ  < \cot 71^\circ $

Câu 14 :

Tính giá trị biểu thức $A = {\sin ^2}1^\circ  + {\sin ^2}2^\circ  + ... + {\sin ^2}88^\circ  + {\sin ^2}89^\circ  + {\sin ^2}90^\circ $

  • A

    $A = 46$

  • B

    $A = \dfrac{{93}}{2}$

  • C

    $A = \dfrac{{91}}{2}$

  • D

    $A = 45$

Câu 15 :

Cho $\alpha $ là góc nhọn bất kỳ. Khi đó $C = {\sin ^4}\alpha  + {\cos ^4}\alpha $ bằng

  • A

    $C = 1 - 2{\sin ^2}\alpha .{\cos ^2}\alpha $

  • B

    $C = 1$

  • C

    $C = {\sin ^2}\alpha .{\cos ^2}\alpha $

  • D

    $C = 1 + 2{\sin ^2}\alpha .{\cos ^2}\alpha $

Câu 16 :

Cho $\alpha $ là góc nhọn bất kỳ. Rút gọn $P = \left( {1 - {{\sin }^2}\alpha } \right).{\cot ^2}\alpha  + 1 - {\cot ^2}\alpha $ ta được

  • A

    $P = {\sin ^2}\alpha $

  • B

    $P = {\cos ^2}\alpha $

  • C

    $P = {\tan ^2}\alpha $

  • D

    $P = 2{\sin ^2}\alpha $

Câu 17 :

Cho $\alpha $ là góc nhọn bất kỳ. Biểu thức $Q = \dfrac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }}$ bằng

  • A

    $Q = 1 + {\tan ^2}\alpha $

  • B

    $Q = 1 + 2{\tan ^2}\alpha $

  • C

    $Q = 1 - 2{\tan ^2}\alpha $

  • D

    $Q = 2{\tan ^2}\alpha $

Câu 18 :

Cho $\tan \alpha  = 2$. Tính giá trị của biểu thức $G = \dfrac{{2\sin \alpha  + \cos \alpha }}{{\cos \alpha  - 3\sin \alpha }}$

  • A

    $G =1$

  • B

    $G =  - \dfrac{4}{5}$

  • C

    $G =  - \dfrac{6}{5}$

  • D

    $G =  - 1$

Câu 19 :

Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 1:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng

  • A

    $2$

  • B

    $3$

  • C

    $1$

  • D

    $4$

Câu 20 :

Cho $ \alpha $ là góc nhọn. Tính \(\cot \alpha \) biết \(\sin \alpha  = \dfrac{5}{{13}}\).

  • A

    $\cot \alpha  = \dfrac{{12}}{5}$

  • B

    $\cot \alpha  = \dfrac{{11}}{5}$

  • C

    $\cot \alpha  = \dfrac{5}{{12}}$

  • D

    $\cot \alpha  = \dfrac{{13}}{5}$

Câu 21 :

Tính giá trị biểu thức $B = \tan 1^\circ .\tan 2^\circ .\tan 3^\circ .....\tan88^\circ .\tan89^\circ $

  • A

    $B = 44$

  • B

    $B = 1$

  • C

    $B = 45$

  • D

    $B = 2$

Câu 22 :

Chọn kết luận đúng về giá trị biểu thức \(B = \dfrac{{{{\cos }^2}\alpha  - 3{{\sin }^2}\alpha }}{{3 - {{\sin }^2}\alpha }}\)  biết \(\tan \alpha  = 3.\)

  • A

    \(B > 0\)

  • B

    \(B < 0\)          

  • C

    \(0 < B < 1\)

  • D

    \(B = 1\)

Câu 23 :

Cho tam giác \(ABC\) cân tại \(A\) có  \(AB = AC = 13cm\); \(BC = 10cm\). Tính \(sinA\).

  • A

    \(\sin A = \dfrac{{120}}{{169}}\)

  • B

    \(\sin A = \dfrac{{60}}{{169}}\)

  • C

    \(\sin A = \dfrac{5}{6}\)

  • D

    \(\sin A = \dfrac{{10}}{{13}}\)

Câu 24 :

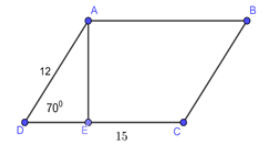
Tính diện tích hình bình hành \(ABCD\) biết \(AD = 12cm;DC = 15cm;\angle ADC = {70^0}\).

  • A

    \(169,1c{m^2}\)

  • B
    \(129,6c{m^2}\)
  • C
    \(116,5c{m^2}\)
  • D
    \(115,8c{m^2}\)
Câu 25 :

Tính số đo góc nhọn \(\alpha \) biết \(10{\sin ^2}\alpha  + 6{\cos ^2}\alpha  = 8\).

  • A
    \(\alpha  = {30^0}.\)
  • B
    \(\alpha  = {45^0}.\)

     

  • C
    \(\alpha  = {60^0}.\)
  • D
    \(\alpha  = {120^0}.\)

Tính giá trị của các biểu thức sau:

Câu 26

\(A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}{55^0} + {\sin ^2}{65^0} + {\sin ^2}{75^0}\) 

  • A.
    \(A=0\)
  • B.

    \(A = \dfrac{7}{2}\)

  • C.

    \(A = -\dfrac{7}{2}\)

  • D.

    \(A = \dfrac{5}{2}\)

Câu 27

\(B = \tan {10^0}.\tan {80^0} - \tan {20^0}.\tan {70^0}.\)

  • A.
    \(B=0\)
  • B.
    \(B=1\)
  • C.

    \(B = \dfrac{7}{2}\)

  • D.

    \(B =- \dfrac{7}{2}\)

Câu 28 :

Biết \({0^0} < \alpha  < {90^0}\). Giá trị bủa biểu thức \(\left[ {\sin \alpha  + 3\,\cos \left( {{{90}^0} - \alpha } \right)} \right]:\left[ {\sin \alpha  - 2\cos \left( {{{90}^0} - \alpha } \right)} \right]\) bằng:

  • A
    \( - 4\)              
  • B
    \(4\)      
  • C

    \(\dfrac{{ - 3}}{2}\)     

  • D

    \(\dfrac{3}{2}\).

Lời giải và đáp án

Câu 1 :

Cho tam giác $MNP$ vuông tại $M$. Khi đó $\cos \widehat {MNP}$ bằng

  • A

    $\dfrac{{MN}}{{NP}}$

  • B

    $\dfrac{{MP}}{{NP}}$

  • C

    $\dfrac{{MN}}{{MP}}$

  • D

    $\dfrac{{MP}}{{MN}}$

Đáp án : A

Lời giải chi tiết :

Ta có $\cos \widehat {MNP} = \dfrac{{MN}}{{NP}}$

Câu 2 :

Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.

  • A

    $\sin \alpha  + \cos \alpha  = 1$

  • B

    ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$

  • C

    ${\sin ^3}\alpha  + {\cos ^3}\alpha  = 1$

  • D

    $\sin \alpha  - cos\alpha  = 1$

Đáp án : B

Phương pháp giải :

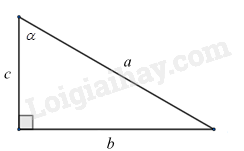
Từ tỉ số lượng giác sin, cos để chứng minh.

Lời giải chi tiết :

Giả sử ta có tam giác vuông có các cạnh và góc $\alpha $ như hình vẽ.

Áp dụng tỉ số lượng giác của góc nhọn, ta có:

$\sin \alpha =\frac{b}{a},\cos \alpha =\frac{c}{a},\tan \alpha =\frac{b}{c},\cot \alpha =\frac{c}{b}$.

Ta có: ${{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha ={{\left( \frac{b}{a} \right)}^{2}}+{{\left( \frac{c}{a} \right)}^{2}}=\frac{{{b}^{2}}+{{c}^{2}}}{{{a}^{2}}}=\frac{{{a}^{2}}}{{{a}^{2}}}=1$

Vậy ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$

Câu 3 :

Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định sai.

  • A

    $\tan \alpha  = \dfrac{{\sin \alpha }}{{\cos \alpha }}\,\,$

  • B

    $\cot \alpha  = \dfrac{{\cos \alpha }}{{\sin \alpha }}\,\,$

  • C

    $\tan \alpha .\cot \alpha  = 1$

  • D

    ${\tan ^2}\alpha  - 1 = {\cos ^2}\alpha $

Đáp án : D

Phương pháp giải :

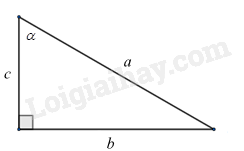
Dựa vào khái niệm tỉ số lượng giác của góc nhọn trong tam giác vuông.

Lời giải chi tiết :

Giả sử ta có tam giác vuông có các cạnh và góc $\alpha $ như hình vẽ.

Áp dụng tỉ số lượng giác của góc nhọn, ta có:

$\sin \alpha =\frac{b}{a},\cos \alpha =\frac{c}{a},\tan \alpha =\frac{b}{c},\cot \alpha =\frac{c}{b}$.

Ta có:

$\tan \alpha =\frac{b}{c}=\frac{b}{a}.\frac{a}{c}=\frac{b}{a}:\frac{c}{a}=\frac{\sin \alpha }{\cos \alpha }$ nên A đúng.

$\cot \alpha =\frac{c}{b}=\frac{c}{a}.\frac{a}{b}=\frac{c}{a}:\frac{b}{a}=\frac{\cos \alpha }{\sin \alpha }$ nên B đúng.

$\tan \alpha .\cot \alpha =\tan \alpha .\frac{1}{\tan \alpha }=1$ nên C đúng.

${{\tan }^{2}}\alpha -1={{\left( \frac{b}{c} \right)}^{2}}-1=\frac{{{b}^{2}}-{{c}^{2}}}{{{c}^{2}}}\ne {{\left( \frac{c}{a} \right)}^{2}}={{\cos }^{2}}\alpha $ nên D sai.

Từ đây, ta có các công thức lượng giác mở rộng sau:

$\tan \alpha =\frac{\sin \alpha }{\cos \alpha };\cot \alpha =\frac{\cos \alpha }{\sin \alpha };\tan \alpha .\cot \alpha =1$

Câu 4 :

Cho $\alpha $ và $\beta $ là hai góc nhọn bất kỳ thỏa mãn $\alpha  + \beta  = 90^\circ $. Khẳng định nào sau đây là đúng?

  • A

    $\tan \alpha  = \sin \beta $

  • B

    $\tan \alpha  = \cot \beta $

  • C

    $\tan \alpha  = \cos \alpha $

  • D

    $\tan \alpha  = \tan \beta $

Đáp án : B

Lời giải chi tiết :

Với hai góc \(\alpha ,\beta \) mà \(\alpha  + \beta  = {90^0}\).

Ta có: \(\sin \alpha  = \cos \beta ;\cos \alpha  = \sin \beta ;\)

\(\tan \alpha  = \cot \beta ;\cot \alpha  = \tan \beta \).

Câu 5 :

Cho tam giác $ABC$ vuông tại  $C$ có \(BC = 1,2\,cm,\,\,AC = 0,9\,cm.\) Tính các tỉ số lượng giác $\sin B;\cos B$ .

  • A

    $\sin B = 0,6;\cos B = 0,8$

  • B

    $\sin B = 0,8;\cos B = 0,6$

  • C

    $\sin B = 0,4;\cos B = 0,8$

  • D

    $\sin B = 0,6;\cos B = 0,4$

Đáp án : A

Phương pháp giải :

Bước 1: Tính cạnh còn lại theo định lý Pytago

Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn

Lời giải chi tiết :

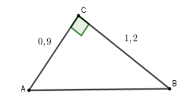Theo định lý Py-ta-go ta có: $A{B^2} = A{C^2} + B{C^2} \Rightarrow AB = \sqrt {0,{9^2} + 1,{2^2}}  = 1,5$

Xét tam giác $ABC$ vuông tại $C$ có $\sin B = \dfrac{{AC}}{{AB}} = \dfrac{{0,9}}{{1,5}} = \dfrac{3}{5} = 0,6$ và $\cos B = \dfrac{{BC}}{{AB}} = \dfrac{{1,2}}{{1,5}} = \dfrac{4}{5} = 0,8$

Câu 6 :

Cho tam giác $ABC$ vuông tại  $A$ có \(BC = 8\,cm,\,\,AC = 6cm.\) Tính tỉ số lượng giác $\tan C$ (làm tròn đến chữ số thập phân thứ $2$ ).

  • A

    $\tan C \approx 0,87$

  • B

    $\tan C \approx 0,86$

  • C

    $\tan C \approx 0,88$

  • D

    $\tan C \approx 0,89$

Đáp án : C

Phương pháp giải :

Bước 1: Tính cạnh còn lại theo định lý Pytago

Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn

Lời giải chi tiết :

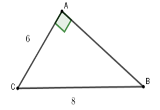Theo định lý Py-ta-go ta có: $B{C^2} = A{C^2} + A{B^2} \Rightarrow AB = \sqrt {{8^2} - {6^2}}  \approx 5,29$

Xét tam giác $ABC$ vuông tại $C$ có $\tan C = \dfrac{{AB}}{{AC}} \approx \dfrac{{5,29}}{6} \approx 0,88.$

Câu 7 :

Trong một hộp thưởng có chứa 5 quả bóng xanh, 20 quả bóng trắng, n quả bóng màu cầu vồng, các quả bóng cùng kích thước. Lấy ngẫu nhiên một quả bóng. Biết xác suất lấy được quả bóng màu cầu vồng là \(\frac{3}{4}\). Tính số quả bóng màu cầu vồng.

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Dựa vào công thức tính xác suất suy ra n:

Xác suất P(E) của biến cố E bằng tỉ số giữa số kết quả thuận lợi cho biến cố E và số phần tử của tập \(\Omega \):

\(P\left( E \right) = \frac{{n\left( E \right)}}{{n\left( \Omega  \right)}}\),

trong đó \(\Omega \) là không gian mẫu của T; n(E) là số kết quả thuận lợi cho biến cố E và \(n\left( \Omega  \right)\) là số phần tử của tập \(\Omega \).

Lời giải chi tiết :

Tổng số quả bóng trong hộp là: \(n + 25\).

Xác suất lấy được quả bóng màu cầu vồng là:

\(\frac{n}{{n + 25}} = \frac{3}{4}\)

Suy ra

\(\begin{array}{l}4n = 3\left( {n + 25} \right)\\4n = 3n + 75\\n = 75\end{array}\)

Đáp án: 75

Câu 8 :

Cho tam giác $ABC$ vuông tại  $A$, đường cao $AH$ có \(CH = 4\,cm,\,BH = 3\,cm.\) Tính tỉ số lượng giác $\cos C$ (làm tròn đến chữ số thập phân thứ $2$ )

  • A

    $\cos C \approx 0,76$

  • B

    $\cos C \approx 0,77$

  • C

    $\cos C \approx 0,75$

  • D

    $\cos C \approx 0,78$

Đáp án : A

Phương pháp giải :

Bước 1: Tính cạnh cần thiết lại theo định lý Pytago hoặc hệ thức lượng trong tam giác vuông.

Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn

Lời giải chi tiết :

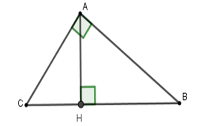Xét tam giác $ABC$ vuông tại $A$ có $BC = BH + CH = 7\,\,cm$

 theo hệ thức lượng trong tam giác vuông ta có $A{C^2} = CH.BC \Rightarrow A{C^2} = 4.7 \Rightarrow AC \approx 5,29\,\,cm$

$ \Rightarrow \cos C = \dfrac{{AC}}{{BC}} = \dfrac{{5,29}}{7} \approx 0,76$.

Câu 9 :

Cho tam giác $ABC$ vuông tại  $A$. Hãy tính $\tan C$ biết rằng \(\cot B = 2\).

  • A

    $\tan C = \dfrac{1}{4}$

  • B

    $\tan C = 4$

  • C

    $\tan C = 2$

  • D

    $\tan C = \dfrac{1}{2}$

Đáp án : C

Phương pháp giải :

Sử dụng nhận xét: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Lời giải chi tiết :

Vì tam giác $ABC$ vuông tại  $A$ nên $\widehat B + \widehat C = 90^\circ $$ \Rightarrow \tan C = \cot B = 2$

Câu 10 :

Cho tam giác $ABC$ vuông tại  $A$ có \(AB = 5\,cm,\,\,\cot C = \dfrac{7}{8}\) . Tính độ dài các đoạn thẳng $AC$ và $BC$ . (làm tròn đến chữ số thập phân thứ $2$ )

  • A

    $AC \approx 4,39 (cm);BC \approx 6,66 (cm)$

  • B

    $AC \approx 4,38(cm);BC \approx 6,64(cm)$

  • C

    $AC \approx 4,38(cm);BC \approx 6,67(cm)$

  • D

    $AC \approx 4,37(cm);BC \approx 6,67(cm)$

Đáp án : B

Phương pháp giải :

Sử dụng tỉ số lương giác của góc nhọn, định lý Pytago để tính cạnh.

Lời giải chi tiết :

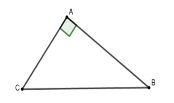Vì tam giác $ABC$ vuông tại  $A$ nên $\cot C = \dfrac{{AC}}{{AB}} \Rightarrow AC = AB.\cot C = 5.\dfrac{7}{8} = \dfrac{{35}}{8} \approx 4,38\,\,cm$

Theo định lý Pytago ta có \(B{C^2} = A{B^2} + A{C^2} = {5^2} + {\left( {\dfrac{{35}}{8}} \right)^2} \Rightarrow BC \approx 6,64\)

Vậy $AC \approx 4,38(cm);BC \approx 6,64(cm)$.

Câu 11 :

Cho $\alpha$ là góc nhọn. Tính \(\sin \alpha,\,\cot \alpha \) biết \(\cos \alpha  = \dfrac{2}{5}\).

  • A

    $\sin \alpha  = \dfrac{{\sqrt {21} }}{{25}};\cot \alpha  = \dfrac{{3\sqrt {21} }}{{21}}$

  • B

    $\sin \alpha  = \dfrac{{\sqrt {21} }}{5};\cot \alpha  = \dfrac{5}{{\sqrt {21} }}$

  • C

    $\sin \alpha  = \dfrac{{\sqrt {21} }}{3};\cot \alpha  = \dfrac{3}{{\sqrt {21} }}$

  • D

    $\sin \alpha  = \dfrac{{\sqrt {21} }}{5};\cot \alpha  = \dfrac{2}{{\sqrt {21} }}$

Đáp án : D

Phương pháp giải :

Sử dụng các hệ thức lượng giác thích hợp

+ Nếu \(\alpha \) là một góc nhọn bất kỳ  thì

\(0 < \sin \alpha  < 1;0 < \cos \alpha  < 1\), \(\tan \alpha  > 0;\cot \alpha  > 0\),  \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\); $\cot \alpha  = \dfrac{{\cos \alpha }}{{\sin \alpha }}$

Lời giải chi tiết :

Ta có ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1 \Rightarrow {\sin ^2}\alpha  = 1 - {\cos ^2}\alpha  = 1 - \dfrac{4}{{25}} = \dfrac{{21}}{{25}}$

$\Rightarrow \sin \alpha  = \dfrac{\sqrt {21}}{5}$

Lại có $\cot \alpha  = \dfrac{{\cos \alpha }}{{\sin \alpha }} = \dfrac{{\dfrac{2}{5}}}{{\dfrac{{\sqrt {21} }}{5}}} = \dfrac{2}{{\sqrt {21} }}$.

Vậy $\sin \alpha  = \dfrac{{\sqrt {21} }}{5};\cot \alpha  = \dfrac{2}{{\sqrt {21} }}$.

Câu 12 :

Không dùng bảng số và máy tính, hãy so sánh \(\sin 20^\circ \) và \(\sin 70^\circ \)

  • A

    $\sin 20^\circ  < \sin 70^\circ $

  • B

    $\sin 20^\circ  > \sin 70^\circ $

  • C

    $\sin 20^\circ  = \sin 70^\circ $

  • D

    $\sin 20^\circ  \ge \sin 70^\circ $

Đáp án : A

Phương pháp giải :

Sử dụng nhận xét : Với góc nhọn \(\alpha ,\,\beta ,\) ta có: $\sin \alpha  < \sin \beta  \Leftrightarrow \alpha  < \beta $

Lời giải chi tiết :

Vì $20^\circ  < 70^\circ  \Leftrightarrow \sin 20^\circ  < \sin 70^\circ $.

Câu 13 :

Sắp xếp các tỉ số lượng giác \(\tan 43^\circ ,\,\,\cot 71^\circ ,\,\,\tan 38^\circ ,\,\,\cot 69^\circ 15',\,\tan 28^\circ \) theo thứ tự tăng dần.

  • A

    $\cot 71^\circ  < \cot 69^\circ 15' < \tan 28^\circ  < \tan 38^\circ  < \tan 43^\circ $

  • B

    $\cot 69^\circ 15' < \cot 71^\circ  < \tan 28^\circ  < \tan 38^\circ  < \tan 43^\circ $

  • C

    $\tan 28^\circ  < \tan 38^\circ  < \tan 43^\circ  < \cot 69^\circ 15' < \cot 71^\circ $

  • D

    $\cot 69^\circ 15' < \tan 28^\circ  < \tan 38^\circ  < \tan 43^\circ  < \cot 71^\circ $

Đáp án : A

Phương pháp giải :

Bước 1 : Đưa các tỉ số lượng giác về cùng loại (sử dụng tính chất "Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia")

Bước 2 : Với góc nhọn \(\alpha ,\,\beta \) ta có: $\tan \alpha  < \tan \beta  \Leftrightarrow \alpha  < \beta $ ; $\cot \alpha  < \cot \beta  \Leftrightarrow \alpha  > \beta $

Lời giải chi tiết :

Ta có $\cot 71^\circ  = \tan 19^\circ \,$ vì $71^\circ  + 19^\circ  = 90^\circ $;  $\cot 69^\circ 15' = \tan 20^\circ 45'$ vì $69^\circ 15' + 20^\circ 45' = 90^\circ $

Mà $ 19^\circ <20^\circ 45'  < 28^\circ  < 38^\circ  < 43^\circ $ nên $ \tan 19^\circ  < \tan 20^\circ 45' <\tan 28^\circ  < \tan 38^\circ  < \tan 43^\circ $

$ \Leftrightarrow  \cot 71^\circ  <\cot 69^\circ 15' < \tan 28^\circ  < \tan 38^\circ  < \tan 43^\circ $

Câu 14 :

Tính giá trị biểu thức $A = {\sin ^2}1^\circ  + {\sin ^2}2^\circ  + ... + {\sin ^2}88^\circ  + {\sin ^2}89^\circ  + {\sin ^2}90^\circ $

  • A

    $A = 46$

  • B

    $A = \dfrac{{93}}{2}$

  • C

    $A = \dfrac{{91}}{2}$

  • D

    $A = 45$

Đáp án : C

Phương pháp giải :

Bước 1 : Đưa các tỉ số lượng giác về cùng một góc hoặc cùng loại  (sử dụng tính chất "Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia")

Bước 2 : Sử dụng đẳng thức lượng giác ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$.

Lời giải chi tiết :

Ta có ${\sin ^2}89^\circ  = {\cos ^2}1^\circ ;{\sin ^2}88^\circ  = {\cos ^2}2^\circ ;...;{\sin ^2}46^\circ  = {\cos ^2}44^\circ $ và ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$

Nên $A = \left( {{{\sin }^2}1^\circ  + {{\sin }^2}89^\circ } \right) + \left( {{{\sin }^2}2^\circ  + {{\sin }^2}88^\circ } \right) + ... + \left( {{{\sin }^2}44^\circ  + {{\sin }^2}46^\circ } \right) + {\sin ^2}45^\circ  + {\sin ^2}90^\circ $

$ = \left( {{{\sin }^2}1^\circ  + {{\cos }^2}1^\circ } \right) + \left( {{{\sin }^2}2^\circ  + {{\cos }^2}2^\circ } \right) + ... + \left( {{{\sin }^2}44^\circ  + {{\cos }^2}44^\circ } \right) + {\sin ^2}45^\circ  + {\sin ^2}90^\circ $

$ = \underbrace {1 + 1 + ... + 1}_{44\,\,so\,1} + \dfrac{1}{2} + 1$$ = 44.1 + \dfrac{3}{2} = \dfrac{{91}}{2}$.

Vậy $A = \dfrac{{91}}{2}.$

Câu 15 :

Cho $\alpha $ là góc nhọn bất kỳ. Khi đó $C = {\sin ^4}\alpha  + {\cos ^4}\alpha $ bằng

  • A

    $C = 1 - 2{\sin ^2}\alpha .{\cos ^2}\alpha $

  • B

    $C = 1$

  • C

    $C = {\sin ^2}\alpha .{\cos ^2}\alpha $

  • D

    $C = 1 + 2{\sin ^2}\alpha .{\cos ^2}\alpha $

Đáp án : A

Phương pháp giải :

Biến đổi để sử dụng các đẳng thức lượng giác thích hợp.

Lời giải chi tiết :

Ta có $C = {\sin ^4}\alpha  + {\cos ^4}\alpha  = {\sin ^4}\alpha  + {\cos ^4}\alpha  + 2{\sin ^2}\alpha .{\cos ^2}\alpha  - 2{\sin ^2}\alpha .{\cos ^2}\alpha $

$ = {\left( {{{\sin }^2}\alpha  + {{\cos }^2}\alpha } \right)^2} - 2{\sin ^2}\alpha .{\cos ^2}\alpha  = 1 - 2{\sin ^2}\alpha .{\cos ^2}\alpha $ (vì ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$)

Vậy $C = 1 - 2{\sin ^2}\alpha .{\cos ^2}\alpha $.

Câu 16 :

Cho $\alpha $ là góc nhọn bất kỳ. Rút gọn $P = \left( {1 - {{\sin }^2}\alpha } \right).{\cot ^2}\alpha  + 1 - {\cot ^2}\alpha $ ta được

  • A

    $P = {\sin ^2}\alpha $

  • B

    $P = {\cos ^2}\alpha $

  • C

    $P = {\tan ^2}\alpha $

  • D

    $P = 2{\sin ^2}\alpha $

Đáp án : A

Phương pháp giải :

Biến đổi để sử dụng các đẳng thức lượng giác thích hợp.

Lời giải chi tiết :

Với $\cot \alpha  = \dfrac{{\cos \alpha }}{{\sin \alpha }};{\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$.

$A = \left( {1 - {{\sin }^2}\alpha } \right).{\cot ^2}\alpha  + 1 - {\cot ^2}\alpha $$ = {\cot ^2}\alpha  - {\sin ^2}\alpha .{\cot ^2}\alpha  + 1 - {\cot ^2}\alpha $

$ = 1 - {\sin ^2}\alpha .\dfrac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = 1 - {\cos ^2}\alpha  = {\sin ^2}\alpha $

Vậy $P = {\sin ^2}\alpha $.

Câu 17 :

Cho $\alpha $ là góc nhọn bất kỳ. Biểu thức $Q = \dfrac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }}$ bằng

  • A

    $Q = 1 + {\tan ^2}\alpha $

  • B

    $Q = 1 + 2{\tan ^2}\alpha $

  • C

    $Q = 1 - 2{\tan ^2}\alpha $

  • D

    $Q = 2{\tan ^2}\alpha $

Đáp án : B

Phương pháp giải :

Biến đổi để sử dụng các đẳng thức lượng giác thích hợp.

Lời giải chi tiết :

Với $\tan \alpha  = \dfrac{{sin\alpha }}{{\cos \alpha }};{\cos ^2}\alpha  = 1 - {\sin ^2}\alpha $.

$Q = \dfrac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }}$$ = \dfrac{{1 - {{\sin }^2}\alpha  + 2{{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }} = \dfrac{{1 - {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }} + \dfrac{{2{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}$

$ = 1 + 2.{\left( {\dfrac{{\sin \alpha }}{{\cos \alpha }}} \right)^2} = 1 + 2{\tan ^2}\alpha $

Vậy $Q = 1 + 2{\tan ^2}\alpha $.

Câu 18 :

Cho $\tan \alpha  = 2$. Tính giá trị của biểu thức $G = \dfrac{{2\sin \alpha  + \cos \alpha }}{{\cos \alpha  - 3\sin \alpha }}$

  • A

    $G =1$

  • B

    $G =  - \dfrac{4}{5}$

  • C

    $G =  - \dfrac{6}{5}$

  • D

    $G =  - 1$

Đáp án : D

Phương pháp giải :

Biến đổi biểu thức đã cho về tỉ số lượng giác cho trước. (sử dụng công thức $\tan \alpha  = \dfrac{{\sin \alpha }}{{\cos \alpha }}$)

Lời giải chi tiết :

Vì $\tan \alpha  = 2$ nên $\cos \alpha  \ne 0$

Ta có $G = \dfrac{{2\sin \alpha  + \cos \alpha }}{{\cos \alpha  - 3\sin \alpha }}$$ = \dfrac{{2\dfrac{{\sin \alpha }}{{\cos \alpha }} + \dfrac{{\cos \alpha }}{{\cos \alpha }}}}{{\dfrac{{\cos \alpha }}{{\cos \alpha }} - 3.\dfrac{{\sin \alpha }}{{\cos \alpha }}}}$$ = \dfrac{{2.\tan \alpha  + 1}}{{1 - 3\tan \alpha }}$

Thay $\tan \alpha  = 2$ ta được $G = \dfrac{{2.2 + 1}}{{1 - 3.2}} =  - \dfrac{5}{5}=-1$.

Vậy $G =  - 1$.

Câu 19 :

Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 1:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng

  • A

    $2$

  • B

    $3$

  • C

    $1$

  • D

    $4$

Đáp án : B

Phương pháp giải :

Sử dụng định nghĩa tỉ số lượng giác của góc nhọn và tam giác đồng dạng.

Lời giải chi tiết :

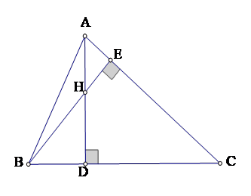Xét tam giác vuông $ABD$ và $ADC$, ta có: \(\tan B = \dfrac{{AD}}{{BD}};tanC = \dfrac{{AD}}{{CD}}\).

Suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{BD.CD}}\)   (1)

Lại có \(\widehat {HBD} = \widehat {CAD}\) (cùng phụ với \(\widehat {ACB}\)) và \(\widehat {HDB} = \widehat {ADC} = {90^0}\).

Do đó \(\Delta BDH \backsim \Delta ADC\) (g.g), suy ra \(\dfrac{{DH}}{{DC}} = \dfrac{{BD}}{{AD}}\), do đó \(BD.DC = DH.AD\)  (2).

Từ (1) và (2) suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{DH.AD}} = \dfrac{{AD}}{{DH}}\)  (3).

Theo giả thiết \(\dfrac{{HD}}{{AH}} = \dfrac{1}{2}\) suy ra \(\dfrac{{HD}}{{AH + HD}} = \dfrac{1}{{2 + 1}}\) hay \(\dfrac{{HD}}{{AD}} = \dfrac{1}{3}\), suy ra \(AD = 3HD\).

Thay vào (3) ta được: \(\tan B.\tan C = \dfrac{{3HD}}{{DH}} = 3\).

Câu 20 :

Cho $ \alpha $ là góc nhọn. Tính \(\cot \alpha \) biết \(\sin \alpha  = \dfrac{5}{{13}}\).

  • A

    $\cot \alpha  = \dfrac{{12}}{5}$

  • B

    $\cot \alpha  = \dfrac{{11}}{5}$

  • C

    $\cot \alpha  = \dfrac{5}{{12}}$

  • D

    $\cot \alpha  = \dfrac{{13}}{5}$

Đáp án : A

Phương pháp giải :

Sử dụng các hệ thức lượng giác thích hợp

+ Nếu \(\alpha \) là một góc nhọn bất kỳ  thì

\(0 < \sin \alpha  < 1;0 < \cos \alpha  < 1\), \(\tan \alpha  > 0;\cot \alpha  > 0\),  \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\); $\cot \alpha  = \dfrac{{\cos \alpha }}{{\sin \alpha }}$

Lời giải chi tiết :

Ta có \(\sin \alpha  = \dfrac{5}{{13}}\) suy ra \({\sin ^2}\alpha  = \dfrac{{25}}{{169}}\), mà \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\), do đó \({\cos ^2}\alpha  = 1 - {\sin ^2}\alpha  = 1 - \dfrac{{25}}{{169}} = \dfrac{{144}}{{169}}\)

Suy ra \(\cos \alpha  = \dfrac{{12}}{{13}}\).

Do đó \(\cot \alpha  = \dfrac{{\cos \alpha }}{{\sin \alpha }} = \dfrac{{12}}{{13}}:\dfrac{5}{{13}} = \dfrac{{12}}{{13}}.\dfrac{{13}}{5} = \dfrac{{12}}{5}\).

Câu 21 :

Tính giá trị biểu thức $B = \tan 1^\circ .\tan 2^\circ .\tan 3^\circ .....\tan88^\circ .\tan89^\circ $

  • A

    $B = 44$

  • B

    $B = 1$

  • C

    $B = 45$

  • D

    $B = 2$

Đáp án : B

Phương pháp giải :

Bước 1 : Đưa các tỉ số lượng giác về cùng một góc hoặc cùng loại (sử dụng tính chất "Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia")

Bước 2 : Sử dụng đẳng thức lượng giác $\tan \alpha .\cot\alpha  = 1$.

Lời giải chi tiết :

Ta có $\tan 89^\circ  = \cot1^\circ ;\tan 88^\circ  = \cot2^\circ ;..;\tan 46^\circ  = \cot44^\circ $ và $\tan \alpha .\cot\alpha  = 1$

Nên $B = \left( {\tan 1^\circ .\tan 89^\circ } \right).\left( {\tan 2^\circ .\tan 88^\circ } \right)....\left( {\tan 46^\circ .\tan 44^\circ } \right).\tan 45^\circ $

$ = \left( {\tan 1^\circ .\cot 1^\circ } \right).\left( {\tan 2^\circ .\cot 2^\circ } \right).\left( {\tan 3^\circ .\cot 3^\circ } \right)....\left( {\tan 44^\circ .\cot 44^\circ } \right).\tan 45^\circ $

$ = 1.1.1....1.1 = 1$

Vậy $B = 1$.

Câu 22 :

Chọn kết luận đúng về giá trị biểu thức \(B = \dfrac{{{{\cos }^2}\alpha  - 3{{\sin }^2}\alpha }}{{3 - {{\sin }^2}\alpha }}\)  biết \(\tan \alpha  = 3.\)

  • A

    \(B > 0\)

  • B

    \(B < 0\)          

  • C

    \(0 < B < 1\)

  • D

    \(B = 1\)

Đáp án : B

Phương pháp giải :

Chia cả tử và mẫu cho \({\cos ^2}\alpha \) rồi sử dung công thức \(\tan \alpha  = \dfrac{{\sin \alpha }}{{\cos \alpha }};\,1 + {\tan ^2}\alpha  = \dfrac{1}{{{{\cos }^2}\alpha }}\) đề biến đổi và tính toán

Lời giải chi tiết :

Vì \(\tan \alpha  = 3 \ne 0 \Rightarrow \cos \alpha  \ne 0.\) Chia cả tử và mẫu của \(B\) cho \({\cos ^2}\alpha \) ta được

\(B = \dfrac{{\dfrac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} - 3\dfrac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}}}{{\dfrac{3}{{{{\cos }^2}\alpha }} - \dfrac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}}} = \dfrac{{1 - 3{{\tan }^2}\alpha }}{{3.\dfrac{1}{{{{\cos }^2}\alpha }} - {{\tan }^2}\alpha }}\)

\( = \dfrac{{1 - 3{{\tan }^2}\alpha }}{{3\left( {1 + {{\tan }^2}\alpha } \right) - {{\tan }^2}\alpha }} = \dfrac{{1 - 3{{\tan }^2}\alpha }}{{3 + 2{{\tan }^2}\alpha }}\)

\( = \dfrac{{1 - 3.9}}{{3 + 2.9}} =  - \dfrac{{26}}{{21}}\)

Hay \(B =  - \dfrac{{26}}{{21}} < 0\)

Câu 23 :

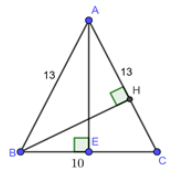
Cho tam giác \(ABC\) cân tại \(A\) có  \(AB = AC = 13cm\); \(BC = 10cm\). Tính \(sinA\).

  • A

    \(\sin A = \dfrac{{120}}{{169}}\)

  • B

    \(\sin A = \dfrac{{60}}{{169}}\)

  • C

    \(\sin A = \dfrac{5}{6}\)

  • D

    \(\sin A = \dfrac{{10}}{{13}}\)

Đáp án : A

Phương pháp giải :

Sử dụng định nghĩa tỉ số lượng giác

Tính chất tam giác cân.

Công thức tính diện tích tam giác

Lời giải chi tiết :

Vì tam giác \(ABC\) cân tại\(A\) nên là \(AE\) đường cao đồng thời là đường trung tuyến

\( \Rightarrow E\) là trung điểm \(BC \Rightarrow EB = EC = 5\)

Xét \(\Delta ABE\) vuông tại \(E\) có:

\(A{E^2} + E{B^2} = A{B^2}\) (Định lý Py-ta-go)

\(A{E^2} + {5^2} = {13^2} \Rightarrow AE = 12\)

\( \Rightarrow {S_{ABC}} = \dfrac{{AE.BC}}{2} = \dfrac{{12.10}}{2} = 60\)

Mặt khác: \({S_{ABC}} = \dfrac{{AC.BH}}{2} \Leftrightarrow 60 = \dfrac{{13.BH}}{2}\)\( \Rightarrow BH = \dfrac{{120}}{{13}}\)

Xét \(\Delta ABH\) vuông tại \(H\) có: \(sinA = \dfrac{{BH}}{{BA}} = \dfrac{{120}}{{13}}:13 = \dfrac{{120}}{{169}}.\)

Câu 24 :

Tính diện tích hình bình hành \(ABCD\) biết \(AD = 12cm;DC = 15cm;\angle ADC = {70^0}\).

  • A

    \(169,1c{m^2}\)

  • B
    \(129,6c{m^2}\)
  • C
    \(116,5c{m^2}\)
  • D
    \(115,8c{m^2}\)

Đáp án : A

Phương pháp giải :

Sử dụng định nghĩa tỉ số lượng giác

Công thức tính diện tích hình bình hành.

Lời giải chi tiết :

Xét \(\Delta ADE\) vuông tại \(E\) có:

\(sinD = \dfrac{{AE}}{{AD}} \Leftrightarrow sin{70^0} = \dfrac{{AE}}{{12}} \Rightarrow AE = 12.sin{70^0}\)

\( \Rightarrow {S_{ABCD}} = AE.DC = 12.\sin {70^0}.15 \approx 169,1\,cm^2\)

Câu 25 :

Tính số đo góc nhọn \(\alpha \) biết \(10{\sin ^2}\alpha  + 6{\cos ^2}\alpha  = 8\).

  • A
    \(\alpha  = {30^0}.\)
  • B
    \(\alpha  = {45^0}.\)

     

  • C
    \(\alpha  = {60^0}.\)
  • D
    \(\alpha  = {120^0}.\)

Đáp án : B

Phương pháp giải :

- Sử dụng công thức \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\) với mọi \( \alpha \).

- Tính \(\sin \alpha \), từ đo suy ra số đo góc \(\alpha \).

Lời giải chi tiết :

Ta có: \(10{\sin ^2}\alpha  + 6{\cos ^2}\alpha  = 8\)

\(\begin{array}{l} \Leftrightarrow 4{\sin ^2}\alpha  + 6\left( {{{\sin }^2}\alpha  + {{\cos }^2}\alpha } \right) = 8\\ \Leftrightarrow 4{\sin ^2}\alpha  + 6 = 8\\ \Leftrightarrow {\sin ^2}\alpha  = \dfrac{1}{2} \Leftrightarrow \sin \alpha  =  \pm \dfrac{{\sqrt 2 }}{2}\end{array}\)

\(Do\,\,\alpha  < {90^0} \Rightarrow \sin \alpha  > 0 \Leftrightarrow \sin \alpha  = \dfrac{{\sqrt 2 }}{2}.\)

Vậy \(\alpha  = {45^0}.\)

Tính giá trị của các biểu thức sau:

Câu 26

\(A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}{55^0} + {\sin ^2}{65^0} + {\sin ^2}{75^0}\) 

  • A.
    \(A=0\)
  • B.

    \(A = \dfrac{7}{2}\)

  • C.

    \(A = -\dfrac{7}{2}\)

  • D.

    \(A = \dfrac{5}{2}\)

Đáp án : B

Phương pháp giải :

Sử dụng các công thức đặc biệt: \(\left\{ \begin{array}{l}\sin \alpha  = \cos \left( {{{90}^0} - \alpha } \right)\\\tan \alpha  = \cot \left( {{{90}^0} - \alpha } \right)\\{\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\\\tan \alpha .\cot \alpha  = 1\end{array} \right..\)

Lời giải chi tiết :

\(\,\,A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}55 + {\sin ^2}{65^0} + {\sin ^2}{75^0}\) 

Ta có:

\(\begin{array}{l}A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}55 + {\sin ^2}{65^0} + {\sin ^2}{75^0}\\\,\,\,\,\, = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\cos ^2}{35^0} + {\cos ^2}{25^0} + {\cos ^2}{15^0}\\\,\,\,\,\, = \left( {{{\sin }^2}{{15}^0} + {{\cos }^2}{{15}^0}} \right) + \left( {{{\sin }^2}{{25}^0} + {{\cos }^2}25} \right) + \left( {{{\sin }^2}{{35}^0} + {{\cos }^2}{{35}^0}} \right) + {\sin ^2}{45^0}\\\,\,\,\, = 1 + 1 + 1 + {\left( {\dfrac{{\sqrt 2 }}{2}} \right)^2} = 3 + \dfrac{1}{2} = \dfrac{7}{2}.\end{array}\) 

Câu 27

\(B = \tan {10^0}.\tan {80^0} - \tan {20^0}.\tan {70^0}.\)

  • A.
    \(B=0\)
  • B.
    \(B=1\)
  • C.

    \(B = \dfrac{7}{2}\)

  • D.

    \(B =- \dfrac{7}{2}\)

Đáp án : A

Phương pháp giải :

Sử dụng các công thức đặc biệt: \(\left\{ \begin{array}{l}\sin \alpha  = \cos \left( {{{90}^0} - \alpha } \right)\\\tan \alpha  = \cot \left( {{{90}^0} - \alpha } \right)\\{\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\\\tan \alpha .\cot \alpha  = 1\end{array} \right..\)

Lời giải chi tiết :

\(\,\,B = \tan {10^0}.\tan {80^0} - \tan {20^0}.\tan {70^0}.\)

Ta có:

\(\begin{array}{l}\,B = \tan {10^0}.\tan {80^0} - \tan {20^0}.\tan {70^0}\\\,\,\,\,\, = \tan {10^0}.\cot{10^0} - \tan {20^0}.\cot {20^0}\\\,\,\,\,\, = 1 - 1 = 0.\end{array}\)

Câu 28 :

Biết \({0^0} < \alpha  < {90^0}\). Giá trị bủa biểu thức \(\left[ {\sin \alpha  + 3\,\cos \left( {{{90}^0} - \alpha } \right)} \right]:\left[ {\sin \alpha  - 2\cos \left( {{{90}^0} - \alpha } \right)} \right]\) bằng:

  • A
    \( - 4\)              
  • B
    \(4\)      
  • C

    \(\dfrac{{ - 3}}{2}\)     

  • D

    \(\dfrac{3}{2}\).

Đáp án : A

Phương pháp giải :

Áp dụng tính chất: \(\sin \alpha  = \cos \left( {{{90}^0} - \alpha } \right);\,\,\,\,\cos \alpha  = \sin \left( {{{90}^0} - \alpha } \right).\)

Lời giải chi tiết :

\(\begin{array}{l}\left[ {\sin \alpha  + 3\,\cos \left( {{{90}^0} - \alpha } \right)} \right]:\left[ {\sin \alpha  - 2\cos \left( {{{90}^0} - \alpha } \right)} \right] \\= \left( {\sin \alpha  + 3\sin \alpha } \right):\left( {\sin \alpha  - 2\sin \alpha } \right)\\ = \left( {4\sin \alpha } \right):\left( { - \sin \alpha } \right) \\=  - 4.\end{array}\)

Bài liên quan
close

Tiện ích | Blog

Nội dung từ Loigiaihay.Com