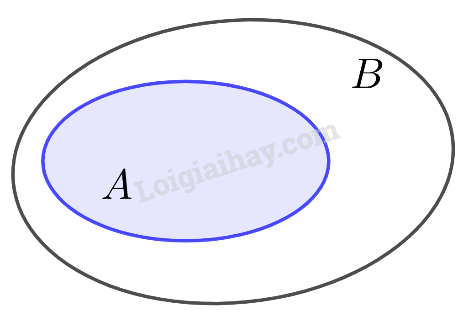
Tập hợp con. Hai tập hợp bằng nhau

1. Lý thuyết

+ Định nghĩa: Tập hợp con

Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con (tập con) của B.

+ Kí hiệu

\(A \subset B\) (đọc là A chứa trong B) hoặc \(B \supset A\)(đọc là B chứa A). 

+ Nhận xét:

    ·  \(A \subset A\) và \(\emptyset  \subset A\) với mọi tập A.

    ·   Nếu A không là tập con của B thì ta viết \(A \not\subset B\)

    ·   Nếu \(A \subset B\) hoặc \(A \subset B\) thì ta nói A và B có quan hệ bao hàm.

+ Số tập hợp con:

Cho tập hợp A có n phần tử, khi đó số tập hợp con của A là: \({2^n}\)

+ Biểu đồ Ven:

Người ta thường minh họa tập hợp bằng một hình phẳng được bao quanh bởi một đường kín.

Theo cách này, ta có thể minh họa A là tập con của B như sau:

+ Mối quan hệ giữa các tập hợp số

\(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\)

+ Kiểm tra A là tập con của B

\(A \subset B \Leftrightarrow \forall x \in A\) suy ra \(x \in B\)

\(A \not\subset B \Leftrightarrow \exists x \in A:x \notin B\)

+ Định nghĩa: Hai tập hợp bằng nhau

Hai tập hợp A và B gọi là bằng nhau nếu mỗi phần tử của A cũng là phần tử của tập hợp B và ngược lại.

+ Kí hiệu: \(A = B\)

+ Nhận xét: \(A = B \Leftrightarrow \left\{ \begin{array}{l}A \subset B\\B \subset A\end{array} \right.\)

2. Ví dụ minh họa

Ví dụ về tập hợp con

Cho tập hợp \(A = \{ 2;3;7\} \)

Các tập \(B = \{ 2\} ,C = \{ 2;7\} \) là các tập con của A. Kí hiệu: \(B \subset A\), \(C \subset A\)

Các tập \(D = \{ 4;5\} ,E = \{ 0\} \) không là tập con của A. Kí hiệu: \(D \not\subset A\), \(E \not\subset A\)

Ví dụ về hai tập hợp bằng nhau

C là tập hợp các hình thoi có hai đường chéo bằng nhau.

D là tập hợp các hình vuông

Ta có: \(C \subset D\) và \(D \subset C\) nên \(C = D\)