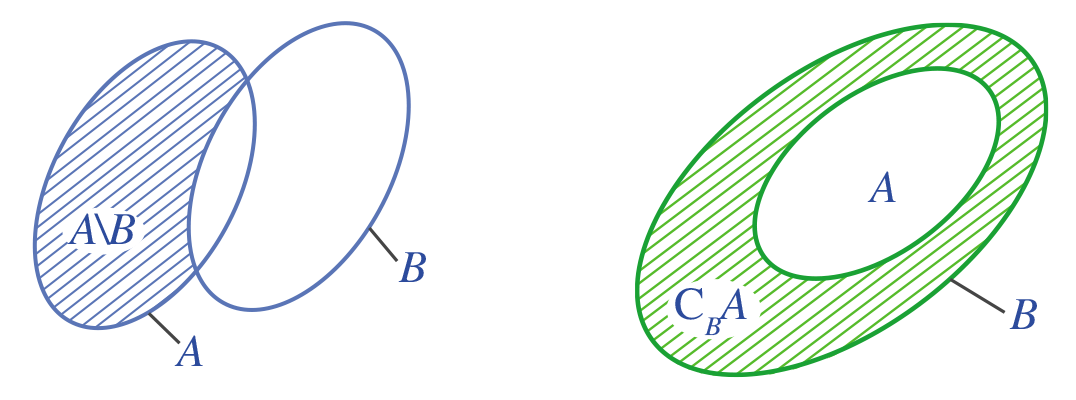
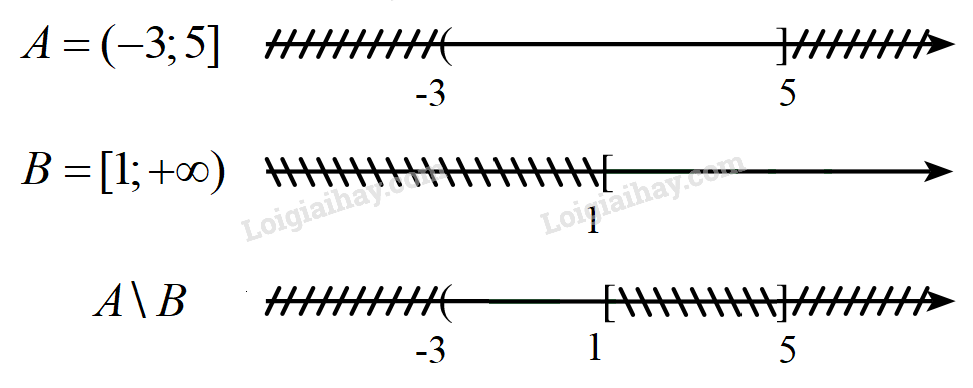
Hiệu của hai tập hợp. Phần bùTập hợp gồm các phần tử thuộc tập hợp A nhưng không thuộc B gọi là hiệu của A và B. Kí hiệu: (A{rm{backslash }}B) 1. Lý thuyết + Định nghĩa: hiệu của A và B Tập hợp gồm các phần tử thuộc tập hợp A nhưng không thuộc B gọi là hiệu của A và B. + Kí hiệu: A∖B Và A∖B={x∈A|x∉B} + Định nghĩa: Phần bù Nếu A⊂B thì hiệu A∖B gọi là phần bù của A trong B. + Kí hiệu: CBA + Biểu đồ Ven + Xác định hiệu của A và B Bước 1: Biểu diễn hai tập hợp đó trên trục số. Bước 2: Gạch bỏ những phần thuộc B trong A. Khi đó phần không bị gạch là hiệu của A và B. 2. Ví dụ minh họa Ví dụ 1. Cho tập hợp C={2;3;5;7} và D={−1;3;4;5;9} Tập hợp C∖D={2;7} Ví dụ 2. Cho tập hợp A=(−3;5] và B=[1;+∞). Xác định A∖B và CR(A∩B).
Vậy A∖B=(−3;1) Ta có: A∩B=(−3;5]∩[1;+∞)=[1;5] Suy ra CR(A∩B)=R∖[1;5]=(−∞;1)∪(5;+∞)  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
