Hàm số. Cách cho một hàm số

1. Lý thuyết

+ Định nghĩa:

Nếu với mỗi giá trị $x$ thuộc tập D, ta xác định được một và chỉ một giá trị tương ứng thuộc tập hợp số thực $\mathbb{R}$ thì ta có một hàm số.

$\Rightarrow$ Nếu với một giá trị của x mà ta tìm được từ 2 giá trị của y thì y không là hàm số của x.

+ Cách gọi: $x$ là biến số, $y$ là hàm số của $x$.

+ Kí hiệu: Thường dùng $y = f(x)$

+ Cách cho một hàm số

Dạng bảng

Ví dụ: Dự báo thời tiết ngày 2/11/2022 tại Hà Nội

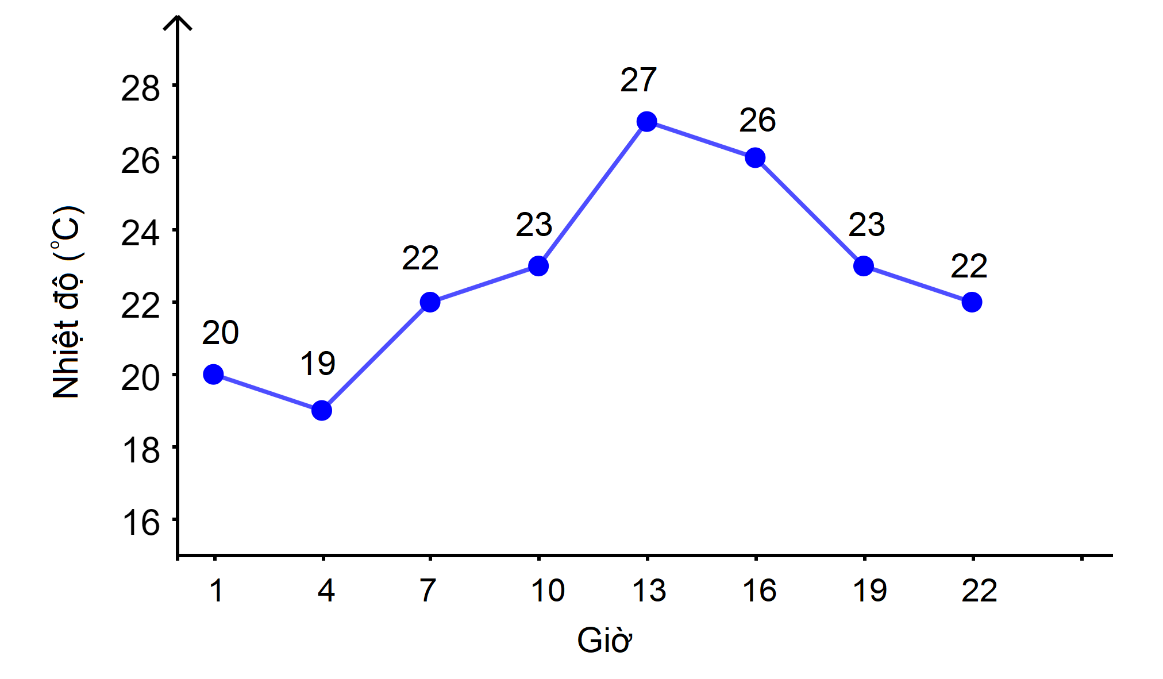
Dạng biểu đồ

Ví dụ: Dự báo thời tiết ngày 20/11/2021 tại Hà Nội

Dạng công thức

Một hàm số có thể được cho bởi một hoặc nhiều công thức.

Chẳng hạn:

$y = {x^2} + 3$

$f(x) = \left\{ \begin{array}{l} - 3x + 5\quad \quad x \le 1\\2{x^2}\quad \quad \quad \;\;x > 1\end{array} \right.$

2. Ví dụ minh họa

+ Hàm số

1. Bảng dưới đây biểu thị một hàm số

$v$ là một hàm số của $t$ vì ứng với mỗi giá trị của t, có một và chỉ một giá trị tương ứng của v.

2. Hàm số cho bởi công thức

$y = \sqrt x  + 4$ với $x \ge 0$

$f(x) = \left\{ \begin{array}{l}1\quad \quad \quad \;\;\quad \quad x \le 0\\2x - 1\quad \quad \quad 0 < x \le 5\\{x^2} - 3x - 1\quad \quad x > 5\end{array} \right.$

+ Không là hàm số

a) Cho bảng sau

$y$ không là hàm số của $x$ vì với $x = 1$ ta xác định được hai giá trị của y là $y = 2$ và $y =  - 1$.

b) Cho $x,y \in \mathbb{R}$ thỏa mãn: ${x^2} + {y^2} = 4$

Khi đó $y$ không là hàm số của $x$ vì với $x = 0$ ta xác định được hai giá trị $y = 2$ và $y =  - 2$ đều thỏa mãn.