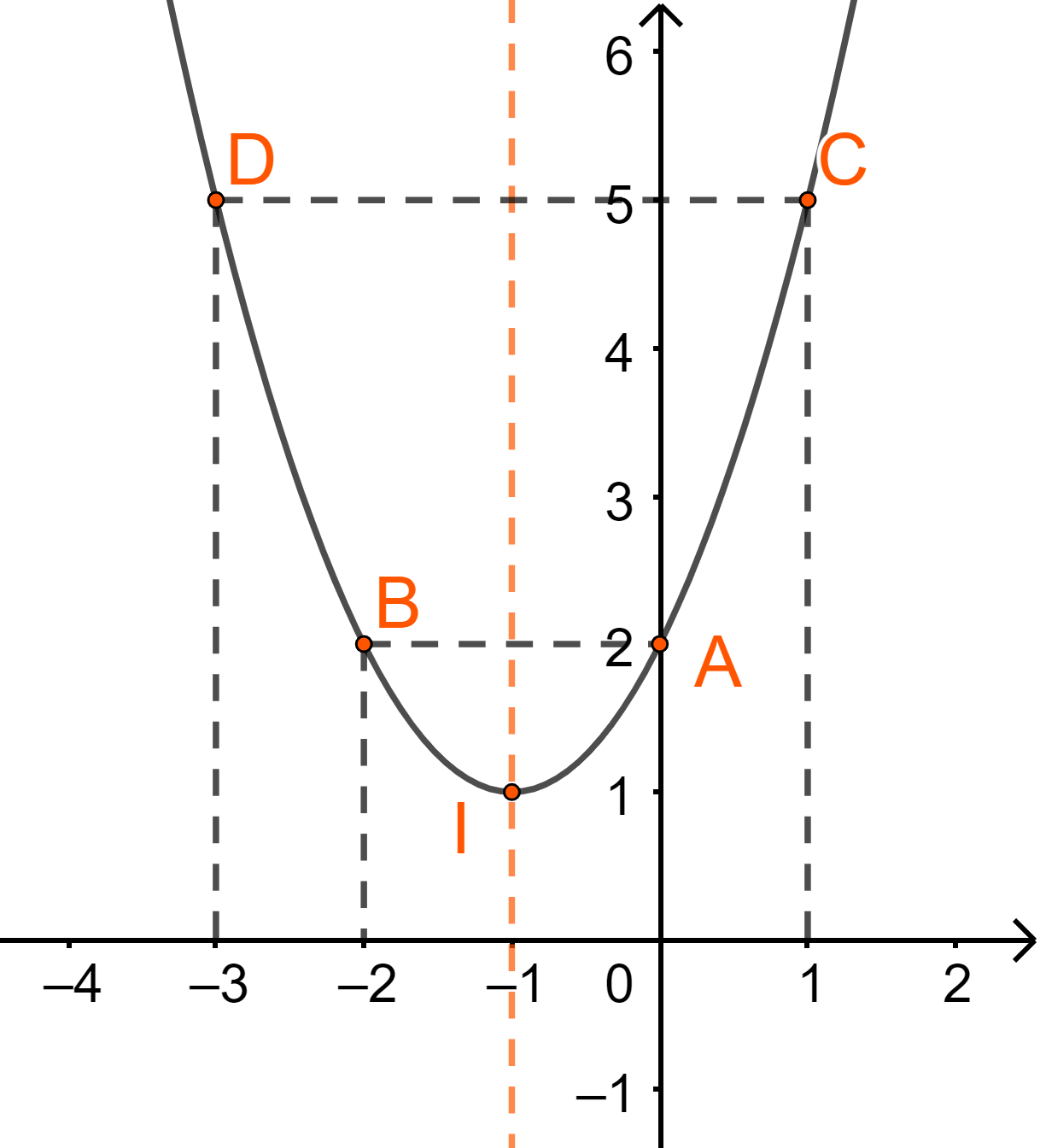
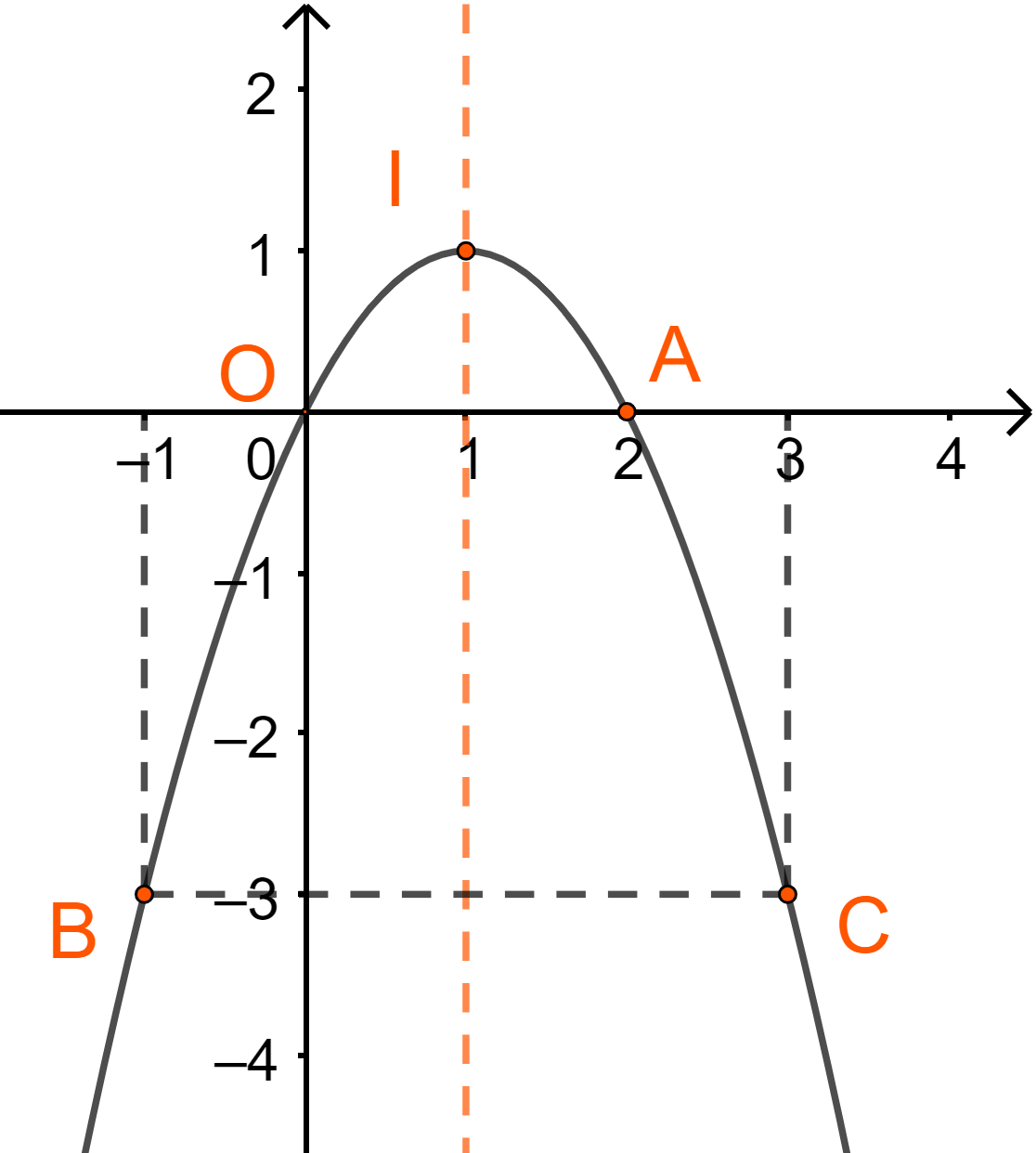
Hàm số bậc hai. Đồ thị hàm số bậc hai.Hàm số bậc hai là hàm số cho bởi công thức y=ax2+bx+c, trong đó x là biến số, a,b,c là hằng số và a≠0. 1. Lý thuyết + Định nghĩa: Hàm số bậc hai là hàm số cho bởi công thức y=ax2+bx+c, trong đó x là biến số, a,b,c là hằng số và a≠0. Tập xác định của hàm số bậc hai là R + Đồ thị hàm số bậc hai Đồ thị hàm số y=ax2+bx+c(a≠0) là một parabol, có đỉnh là điểm I(−b2a;−b2−4ac4a), có trục đối xứng là đường thẳng x=−b2a. Parabol này quay bề lõm lên trên nếu a>0, xuống dưới nếu a<0. + Các bước vẽ đồ thị hàm số y=ax2+bx+c Bước 1: Xác định a,b,c từ đó suy ra tọa độ đỉnh I(−b2a;−b2−4ac4a) Bước 2: Xác định trục đối xứng x=−b2a Bước 3: Xác định giao điểm của parabol với trục tung, trục hoành (nếu có) và vài điểm đặc biệt (đối xứng nhau qua trục đối xứng) trên parabol Bước 4: Vẽ parabol. 2. Ví dụ minh họa Ví dụ 1. Vẽ đồ thị hàm số y=x2+2x+2 Hàm số y=x2+2x+2 có a=1,b=2,c=2 ⇒−b2a=−22.1=−1;y(−1)=(−1)2+2.(−1)+2=1 + Tọa độ đỉnh I(−1;1) + Trục đối xứng x=−1 + Giao điểm với trục tung là A(0;2), không cắt trục hoành (vì y=x2+2x+2=(x+1)2+1>0∀x∈R) + Lấy điểm B(-2;2) đối xứng với A(0;2) qua trục đối xứng. Điểm C(1;5), D(-3;5) thuộc đồ thị. Ví dụ 2. Vẽ đồ thị hàm số y=−x2+2x Hàm số y=−x2+2x có a=−1,b=2,c=0 ⇒−b2a=−22.(−1)=1;y(1)=−12+2.1=1 + Tọa độ đỉnh I(1;1) + Trục đối xứng x=1 + Giao điểm với trục tung là O(0;0), điểm giao với trục hoành là A(2;0) + Lấy điểm B(-1;-3) thuộc đồ thị. Điểm C(3;-3) đối xứng với B(-1;-3) qua trục đối xứng
|