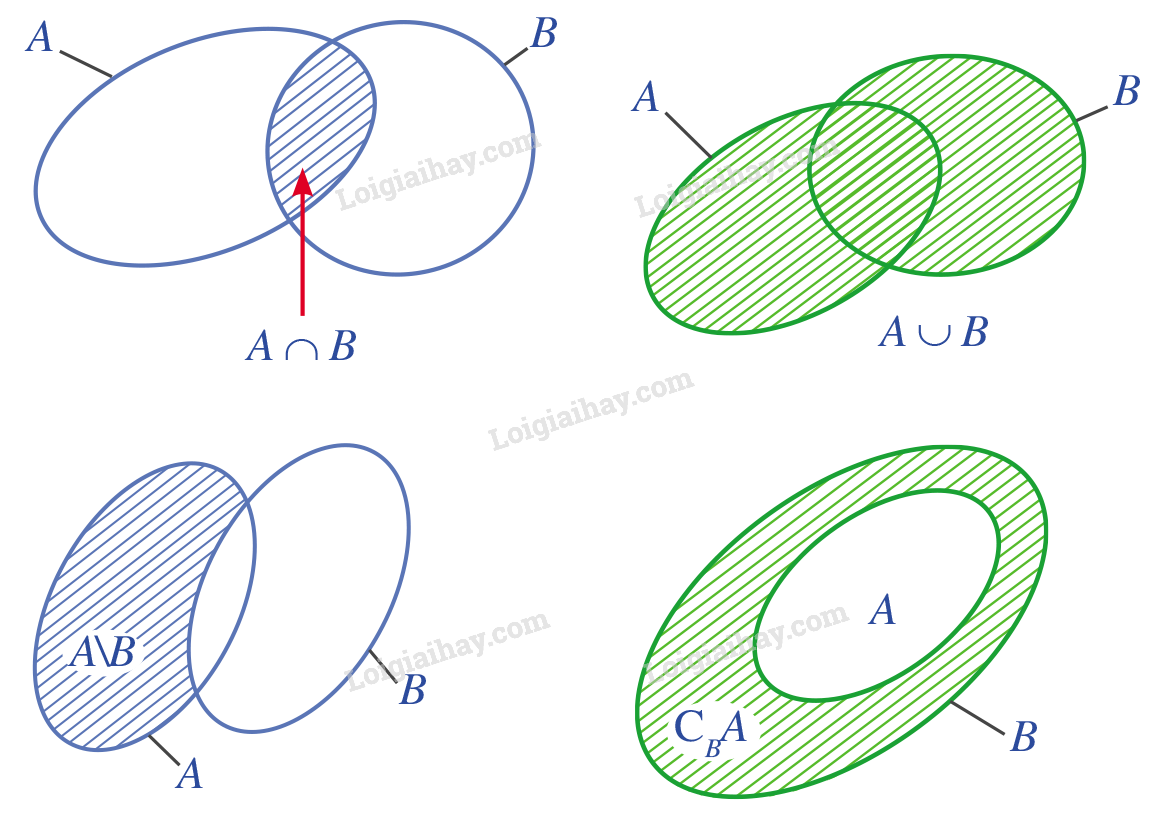
Các phép toán trên tập hợp

1. Lý thuyết

+ Phép giao

Tập hợp gồm các phần tử thuộc cả hai tập hợp A và B gọi là giao của hai tập hợp A và B. Kí hiệu: $A \cap B$

$A \cap B = \{ x|x \in A$ và $x \in B\}$

+ Phép hợp

Tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc tập hợp B gọi là hợp của hai tập hợp A và B. Kí hiệu: $A \cup B$

$A \cup B = \{ x|x \in A$ hoặc $x \in B\}$

+ Hiệu của A và B

Tập hợp gồm các phần tử thuộc tập hợp A nhưng không thuộc B gọi là hiệu của A và B. Kí hiệu: $A{\rm{\backslash }}B$.

$A{\rm{\backslash }}B = \{ x \in A|x \notin B\}$

+ Phần bù

Nếu $A \subset B$ thì hiệu $A{\rm{\backslash }}B$ gọi là phần bù của A trong B. Kí hiệu: ${C_B}A$

+ Biểu đồ Ven

 + Mối quan hệ về số phần tử

$n\left( {A \cup B} \right) = n(A) + n(B) - n(A \cap B)$

$n(A{\rm{\backslash }}B) = n(A) - n(A \cap B)$

2. Ví dụ minh họa

Ví dụ 1. Cho hai tập hợp $A = \left[ { - 2;{\mkern 1mu} {\mkern 1mu} 3} \right)$ và $B = \left[ {1;6} \right)$.

Xác định các tập hợp $A \cup B,A \cap B,A{\rm{\backslash }}B,B{\rm{\backslash }}A$

 $A \cup B = [ - 2;6)$

$A \cap B = [ - 1;3)$

$A\backslash B = [ - 2; - 1)$

$B\backslash A = [3;6)$

Ví dụ 2. Cho hai tập hợp $A = ( - 1;4]$ và $B = [ - 2; + \infty )$. Xác định tập hợp ${C_B}A$.

Ta có: ${C_B}A = B\backslash A = [ - 2; + \infty ){\rm{\backslash }}( - 1;4]$

$\Rightarrow {C_B}A = [ - 2; - 1] \cup (4; + \infty ).$