Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho tam giác \(ABC\) vuông tại \(A\), có đường cao \(AH\) (\(H\)thuộc \(BC\)). Biết độ dài đoạn \(AB\) bằng \(5cm\), đoạn \(BH\) bằng \(3cm\). Tính độ dài các cạnh \(AC\) và \(BC\).
- A \(BC = \dfrac{{20}}{3}cm,AC = \dfrac{{25}}{3}cm.\)
- C \(BC = \dfrac{{22}}{3}cm,AC = \dfrac{{20}}{3}cm.\)
- C \(BC = \dfrac{{20}}{3}cm,AC = \dfrac{{22}}{3}cm.\)
- D \(BC = \dfrac{{25}}{3}cm,AC = \dfrac{{20}}{3}cm.\)
25 bài tập vận dụng Một số hệ thức về cạnh và đường cao trong tam giác vuông
Câu hỏi:
Rút gọn các biểu thức sau:
Câu 1:
\(P = \left( {\dfrac{{2 - \sqrt 2 }}{{\sqrt 2 - 1}} + 1} \right)\left( {\sqrt 2 - 1} \right)\)
- A \(P = \sqrt 2\)
- B \(P = 1\)
- C \(P = - \sqrt 2\)
- D \(P = - 1\)
Câu 2:
\(Q = \left( {\dfrac{1}{{\sqrt x + 3}} - \dfrac{1}{{\sqrt x }}} \right)\left( {\dfrac{3}{{\sqrt x }} + 1} \right)\) với \(x > 0\)
- A \(Q = - \dfrac{3}{x}\)
- B \(Q = \dfrac{3}{x}\)
- C \(Q = - \dfrac{1}{x}\)
- D \(Q = \dfrac{1}{x}\)
Câu hỏi:
Cho tam giác \(ABC\) vuông tại \(A.\) Biết \(AB = 6cm,\,AC = 8cm.\)
Câu 1:
Tính độ dài cạnh \(BC.\)
- A \(BC = 8,5cm\)
- B \(BC = 9cm\)
- C \(BC = 10cm\)
- D \(BC = 12cm\)
Câu 2:
Kẻ đường cao \(AH.\) Tính độ dài đoạn \(AH.\)
- A \(AH = 3,6cm\)
- B \(AH = 4,8cm\)
- C \(AH = 5,4cm\)
- D \(AH = 4,2cm\)
25 bài tập vận dụng Một số hệ thức về cạnh và đường cao trong tam giác vuông
Câu hỏi:
Tìm \(a\) để đồ thị hàm số \(y = ax + 5\) đi qua điểm \(M\left( {3; - 1} \right)\).
- A \(a = - 2\)
- C \(a = 2\)
- C \(a = 1\)
- D \(a = - 1\)
Câu hỏi:
Thực hiện phép tính: \(5\sqrt 9 - 3\sqrt 4 .\)
- A \(6\)
- C \(9\)
- C \(5\)
- D \(8\)
Câu hỏi:
Gọi \(S\) là tập các giá trị của \(m\) để đường thẳng \(y = mx + 3\) cắt trục \(Ox\) và trục \(Oy\) lần lượt tại \(A\) và \(B\) sao cho tam giác \(AOB\) cân. Tính tổng các phần tử của \(S.\)
- A \(1.\)
- C \(3.\)
- C \( - 1.\)
- D \(0.\)
20 bài tập tổng hợp về Hệ số góc của đường thẳng y=ax+b (a khác 0)
Câu hỏi:
Một học sinh dùng kế giác, đứng cách chân cột cờ \(10m\) rồi chỉnh mặt thước ngắm cao bằng mắt của mình để xác định góc "nâng" (góc tạo bởi tia sáng đi thẳng từ đỉnh cột cờ với mắt tạo với phương nằm ngang). Khi đó, góc "nâng" đo được \({31^0}\). Biết khoảng cách từ mặt sân đến mắt học sinh đó bằng \(1,5m\). Tính chiều cao cột cờ (kết quả làm tròn đến một chữ số thập phân).
- A \(6,0m.\)
- C \(16,6m.\)
- C \(7,5m.\)
- D \(5,0m.\)
15 bài tập vận dụng về Ứng dụng thực tế các tỉ số lượng giác của góc nhọn
Câu hỏi:
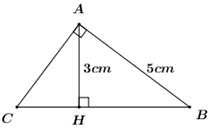
Trong hình vẽ bên, tam giác \(ABC\) vuông tại \(A,\) cạnh \(AB = 5cm,\) đường cao \(AH = 3cm.\) Độ dài cạnh \(BC\)bằng
- A \(\dfrac{4}{{15}}\,cm.\)
- C \(4cm.\)
- C \(\dfrac{{25}}{4}cm.\)
- D \(\dfrac{{25}}{{16}}cm.\)
20 bài tập cơ bản Một số hệ thức về cạnh và đường cao trong tam giác vuông
Câu hỏi:
Có bao nhiêu giá trị của \(x\) để \(A = \dfrac{{4\sqrt x + 16}}{{\sqrt x + 2}}\) (với \(x \ge 0\)) nhận giá trị nguyên?
- A \(6.\)
- C \(4.\)
- C \(8.\)
- D \(3.\)
Câu hỏi:
Khoảng cách lớn nhất từ gốc tọa độ \(O\) đến đường thẳng \(\left( d \right):y = \left( {m - 1} \right)x + 4m\) là
- A \(2\sqrt 2 .\)
- C \(8\sqrt 2 .\)
- C \(4\sqrt 2 \).
- D \(4.\)