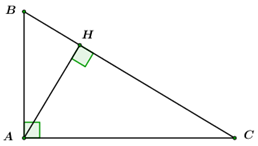
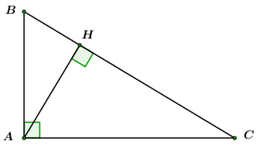
20 bài tập cơ bản Một số hệ thức về cạnh và đường cao trong tam giác vuôngLàm bàiCâu hỏi 1 : Cho \(\Delta ABC\) vuông tại \(A,\) đường cao \(AH\) . Hệ thức nào sau đây sai?
Đáp án: A Phương pháp giải: Sử dụng các hệ thức lượng trong tam giác vuông. Lời giải chi tiết: Tam giác \(ABC\) vuông tại \(A,\,\,\) đường cao \(AH\). \( \Rightarrow \frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Rightarrow \) Đáp án A sai. Chọn A. Câu hỏi 2 : Cho \(\Delta ABC\) vuông tại\(A,\) đường cao \(AH.\) Khẳng định bào sau đây đúng?
Đáp án: C Phương pháp giải: Áp dụng các công thức hệ thức lượng trong tam giác vuông để làm bài. Lời giải chi tiết: Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(A{H^2} = HB.HC.\) Chọn C. Câu hỏi 3 : Cho \(\Delta ABC\) vuông tại \(A,\) có \(\frac{{AB}}{{AC}} = \frac{5}{7},\) đường cao \(AH = 15cm.\) Câu 1: Tính \(HB\)
Đáp án: A Phương pháp giải: Sử dụng hệ thức lượng trong tam giác vuông \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\) để làm bài toán. Lời giải chi tiết: Câu 2: Tính \(HC\).
Đáp án: D Phương pháp giải: Sử dụng hệ thức lượng trong tam giác vuông \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\) để làm bài toán. Lời giải chi tiết: Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(\begin{array}{l} Câu hỏi 4 : Cho \(\Delta ABC\) vuông tại \(A,\,\,AB = 12\,\,cm,\,\,AC = 16\,cm\) và đường phân giác \(AD,\) đường cao \(AH.\) Câu 1: Tính \(HA\)?
Đáp án: D Phương pháp giải: Sử dụng định lý Pitago, các công thức hệ thức lượng trong tam giác vuông và tính chất tia phân giác của một góc trong tam giác để làm bài toán. Lời giải chi tiết: Áp dụng định lý Pitago trong \(\Delta ABC\) vuông tại \(A\) ta có: \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{12}^2} + {{16}^2}} = 20\,\,cm.\) Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(\begin{array}{l}\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{{{12}^2}}} + \frac{1}{{{{16}^2}}} = \frac{{25}}{{2304}}\\ \Rightarrow A{H^2} = \frac{{2304}}{{25}} \Rightarrow AH = 9,6\,\,cm.\end{array}\) Câu 2: Tính \(HB\)?
Đáp án: A Phương pháp giải: Sử dụng định lý Pitago, các công thức hệ thức lượng trong tam giác vuông và tính chất tia phân giác của một góc trong tam giác để làm bài toán. Lời giải chi tiết: Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(\begin{array}{l}A{B^2} = BH.BC \Rightarrow HB = \frac{{A{B^2}}}{{BC}} = \frac{{{{12}^2}}}{{20}} = 7,2\,\,\,cm.\end{array}\) Câu 3: Tính \(HC\)?
Đáp án: C Phương pháp giải: Sử dụng định lý Pitago, các công thức hệ thức lượng trong tam giác vuông và tính chất tia phân giác của một góc trong tam giác để làm bài toán. Lời giải chi tiết: Ta có: \(BC = HB + HC \Rightarrow HC = BC - HB = 20 - 7,2 = 12,8\,\,cm\) Câu 4: Tính \(HD\)?
Đáp án: B Phương pháp giải: Sử dụng định lý Pitago, các công thức hệ thức lượng trong tam giác vuông và tính chất tia phân giác của một góc trong tam giác để làm bài toán. Lời giải chi tiết: Ta có \(AD\) là phân giác của \(\angle BAC\) nên áp dụng tính chất tia phân giác ta có: \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{DC}} = \frac{{12}}{{16}} = \frac{3}{4} \Rightarrow BD = \frac{3}{4}DC.\) Lại có: \(BD + DC = BC \Leftrightarrow \frac{3}{4}DC + DC = 20 \Leftrightarrow DC = \frac{{80}}{7}\,\,\,cm.\) \(\begin{array}{l} \Rightarrow BD = \frac{3}{4}.\frac{{80}}{7} = \frac{{60}}{7}\,\,cm.\\ \Rightarrow HD = BD - BH = \frac{{60}}{7} - 7,2 = \frac{{25}}{{21}} \approx 1,2\,\,cm.\end{array}\) Câu hỏi 5 : Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Hệ thức nào trong các hệ thức sau là đúng ?
Đáp án: D Phương pháp giải: Sử dụng hệ thức lượng trong tam giác vuông Lời giải chi tiết: Xét tam giác \(ABC\) vuông tại \(A,\) chiều cao \(AH.\) Theo hệ thức lượng trong tam giác vuông ta có: \(AH.BC = AB.AC\) nên D đúng. Chọn D Câu hỏi 6 : Cho \(\Delta ABC\) có \(AB = 3cm,\,\,AC = 4cm,\,\,BC = 5cm.\) Phát biểu nào dưới đây đúng?
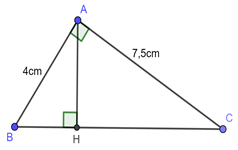
Đáp án: A Phương pháp giải: Sử dụng định lý Pitago đảo để làm bài toán. Tam giác \(ABC\) có độ dài các cạnh lần lượt là \(a,\,\,b,\,\,c\) có \({a^2} = {b^2} + {c^2}\) thì \(\Delta ABC\) vuông. Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l}A{B^2} = {3^2} = 9\\A{C^2} = {4^2} = 16\\B{C^2} = {5^2} = 25\end{array} \right. \Rightarrow B{C^2} = A{B^2} + A{C^2} = 25\) \( \Rightarrow \Delta ABC\) là tam giác vuông tại \(A.\) (định lý Pitago đảo) Chọn A. Câu hỏi 7 : Cho tam giác \(ABC\) vuông tại \(A\) , kẻ đường cao \(AH\). Biết \(AB = 4cm,AC = 7,5cm\). Tính \(HB,HC\).
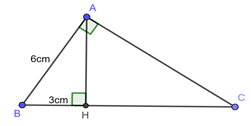
Đáp án: A Phương pháp giải: Sử dụng định lý Pitago cho tam giác ABC vuông ở A để tính độ dài cạnh BC. Áp dụng công thức hệ thức lượng trong tam giác vuông để tính cạnh \(BH:\,\,\,\,A{B^2} = BH.BC.\) Từ đó suy ra độ dài cạnh \(HC:\,\,\,HC = BC - HB.\) Lời giải chi tiết: Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {4^2} + 7,{5^2} = \frac{{289}}{4} \Rightarrow BC = 8,5\left( {cm} \right)\) Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \( \Rightarrow A{B^2} = BH.BC\) \( \Leftrightarrow {4^2} = 8,5.BH \Leftrightarrow BH = \frac{{32}}{{17}}\,\,\,\left( {cm} \right)\) Ta có: \(CH = BC - BH = 8,5 - \frac{{32}}{{17}} = \frac{{225}}{{34}}\left( {cm} \right)\) Chọn A. Câu hỏi 8 : Cho tam giác \(ABC\) vuông tại \(A\) , kẻ đường cao \(AH\). Biết \(AB = 6cm,\,\,\,BH = 3cm.\) Tính \(AH,AC,BC.\)
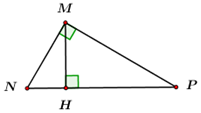
Đáp án: B Phương pháp giải: Sử dụng định lý Pitago cho tam giác ABH vuông ở H để tính độ dài cạnh AH. Áp dụng công thức hệ thức lượng trong tam giác vuông để tính cạnh \(AC:\,\,\,\,\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}.\) Sử dụng định lý Pitago cho tam giác ABC vuông ở A để tính độ dài cạnh BC. Lời giải chi tiết: Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(H\) có: \(A{H^2} + H{B^2} = A{B^2}\) \(\begin{array}{l} \Leftrightarrow A{H^2} + 9 = 36 \Leftrightarrow A{H^2} = 36 - 9 = 27\\ \Rightarrow AH = \sqrt {27} = 3\sqrt 3 \left( {cm} \right)\end{array}\) Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \( \Rightarrow \frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\) \( \Leftrightarrow \frac{1}{{27}} = \frac{1}{{{6^2}}} + \frac{1}{{A{C^2}}}\) \( \Leftrightarrow \frac{1}{{A{C^2}}} = \frac{1}{{108}} \Leftrightarrow A{C^2} = 108 \Leftrightarrow AC = 6\sqrt 3 \left( {cm} \right)\) Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\) (Định lý Pi-ta-go) \( \Leftrightarrow B{C^2} = {6^2} + 108 = 144 \Rightarrow BC = 12\,\,\left( {cm} \right)\) Chọn B. Câu hỏi 9 : Cho \(\Delta MNP\) vuông tại \(M\), đường cao \(MH\). Khẳng định nào sau đây đúng?
Đáp án: C Phương pháp giải: Sử dụng hệ thức lượng trong tam giác vuông. Lời giải chi tiết: Xét tam giác \(MNP\) vuông tại \(M\), đường cao \(MH\) ta có: \(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{M{N^2}}} + \dfrac{1}{{M{P^2}}}\). Vậy khẳng định C đúng. Chọn C. Câu hỏi 10 : Cho tam giác MNP vuông tại M, đường cao MH. Chọn hệ thức sai:
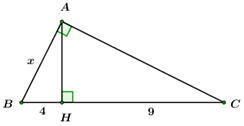
Đáp án: B Phương pháp giải: Sử dụng công thức hệ thức lượng trong tam giác vuông. Lời giải chi tiết: Áp dụng hệ thức lượng trong tam giác MNP vuông tại M, đường cao MH có: \(M{H^2} = HN.HP.\) Chọn B. Câu hỏi 11 : Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH,\) biết \(BH = 4,\,\,HC = 9.\) Đặt \(AB = x,\) tính \(x.\)
Đáp án: D Phương pháp giải: Sử dụng hệ thức lượng trong tam giác vuông để làm bài. Lời giải chi tiết: Ta có: \(BC = BH + HC = 4 + 9 = 13.\) Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A,\) đường cao \(AH\) ta có: \(A{B^2} = BH.BC \Leftrightarrow {x^2} = 4.13 \Rightarrow x = 2\sqrt {13} .\) Chọn D. Câu hỏi 12 : Cho \(\Delta ABC\) có \(AB = 5\,cm,\,\,\,AC = 12cm,\,\,BC = 13\,cm\) và đường cao \(AH.\) Câu 1: Tính độ dài cạnh \(HA\)?
Đáp án: B Phương pháp giải: Sử dụng định lý Pitago đảo để chứng minh\(\Delta ABC\) là tam giác vuông. Sử dụng các công thức hệ thức lượng trong tam giác vuông để tính các cạnh đề bài yêu cầu. Lời giải chi tiết: Ta có: \(A{B^2} + A{C^2} = {5^2} + {12^2} = 169 = {13^2} = B{C^2}\) \( \Rightarrow \Delta ABC\) là tam giác vuông tại \(A\) (định lý Pitago đảo). Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(\begin{array}{l}AH.BC = AB.AC \Leftrightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{5.12}}{{13}} = \frac{{60}}{{13}}\,\,(cm).\end{array}\) Câu 2: Tính độ dài cạnh \(HB\)?
Đáp án: A Phương pháp giải: Sử dụng định lý Pitago đảo để chứng minh\(\Delta ABC\) là tam giác vuông. Sử dụng các công thức hệ thức lượng trong tam giác vuông để tính các cạnh đề bài yêu cầu. Lời giải chi tiết: Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(\begin{array}{l}A{B^2} = HB.BC \Rightarrow HB = \frac{{A{B^2}}}{{BC}} = \frac{{{5^2}}}{{13}} = \frac{{25}}{{13}}\,\,cm.\end{array}\) Câu 3: Tính độ dài cạnh \(HC\)?
Đáp án: C Phương pháp giải: Sử dụng định lý Pitago đảo để chứng minh\(\Delta ABC\) là tam giác vuông. Sử dụng các công thức hệ thức lượng trong tam giác vuông để tính các cạnh đề bài yêu cầu. Lời giải chi tiết: Ta có: \(HC = BC - HB = 13 - \frac{{25}}{{13}} = \frac{{144}}{{13}}\,\,cm\) Câu hỏi 13 : Cho \(\Delta ABC\) vuông tại \(A,\) có \(BC = 24\,cm\) và đường cao \(AH.\) Biết \(AB = \frac{2}{3}AC.\) Câu 1: Tính số đo các góc \(B,\,\,C\) của \(\Delta ABC\).
Đáp án: B Phương pháp giải: Sử dụng các công thức tỉ số lượng giác của góc nhọn trong tam giác vuông. Lời giải chi tiết: Ta có: \(\frac{{AB}}{{AC}} = \frac{2}{3} \Leftrightarrow AB = \frac{2}{3}AC.\) \(\begin{array}{l} \Rightarrow \tan \angle B = \frac{{AC}}{{AB}} = \frac{3}{2} \Rightarrow \angle B \approx {56^0}18'\\ \Rightarrow \angle C = {90^0} - \angle B = {90^0} - {56^0}18' = {33^0}42'.\end{array}\) Câu 2: Tính độ dài \(AC\).
Đáp án: A Phương pháp giải: Sử dụng định lý Pitago trong tam giác vuông để làm bài. Lời giải chi tiết: Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) ta có: \(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} \Leftrightarrow {24^2} = {\left( {\frac{2}{3}AC} \right)^2} + A{C^2}\\ \Leftrightarrow \frac{{13}}{9}A{C^2} = 576 \Leftrightarrow A{C^2} = \frac{{5184}}{{13}} \Rightarrow AC = \frac{{72\sqrt {13} }}{{13}}\,\,cm.\end{array}\) Câu 3: Tính độ dài \(AB\).
Đáp án: A Phương pháp giải: Cộng trừ độ dài các đoạn thẳng. Lời giải chi tiết: Ta có: \( AB = \frac{2}{3}.\frac{{72\sqrt {13} }}{{13}}\, = \frac{{144\sqrt {13} }}{{39}} = \frac{{48\sqrt {13} }}{{13}}\,\,cm.\) Câu 4: Tính độ dài \(AH \).
Đáp án: C Phương pháp giải: Sử dụng hệ thức lượng trong tam giác vuông để làm bài. Lời giải chi tiết: Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(AH.BC = AB.AC \Leftrightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{\frac{{144\sqrt {13} }}{{39}}.\frac{{72\sqrt {13} }}{{13}}}}{{24}} = \frac{{144}}{{13}}\,\,cm.\) Câu hỏi 14 : Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Hệ thức nào dưới đây SAI?
Đáp án: B Phương pháp giải: Áp dụng các hệ thức lượng trong tam giác. Lời giải chi tiết: Ý A: đúng Ý B: Sai. Công thức đúng là theo định lý Pytago: \(B{C^2} = A{B^2} + A{C^2}\) Ý C: đúng Ý D: đúng Chọn B Câu hỏi 15 : Cho tam giác \(ABC\) vuông tại \(A,\) biết \(AB = 6cm,\) \(AC = 8cm.\) Khi đó độ dài đoạn thẳng \(BC\) bằng
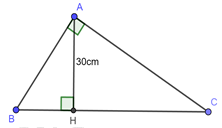
Đáp án: A Phương pháp giải: Sử dụng định lý Pytago để tính cạnh \(BC.\) Lời giải chi tiết: Xét tam giác \(ABC\) vuông tại \(A\), theo định lý Pytago ta có: \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{6^2} + {8^2}} = 10\,\,cm.\) Chọn A Câu hỏi 16 : Cho tam giác \(ABC\) vuông tại \(A.\) Biết \(\frac{{AB}}{{AC}} = \frac{5}{6}\), đường cao \(AH = 30cm\). Tính \(BH,HC\).
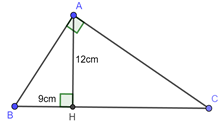
Đáp án: B Phương pháp giải: Áp dụng công thức hệ thức lượng trong tam giác vuông để tính cạnh \(AC:\,\,\,\,\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}.\) Kết hợp với giả thiết \(\frac{{AB}}{{AC}} = \frac{5}{6}\) để tính các cạnh \(AB,\,\,AC.\) Áp dụng công thức hệ thức lượng trong tam giác vuông để tính cạnh \(HB:\,\,\,A{B^2} = HB.BC \Rightarrow HC.\) Lời giải chi tiết: Ta có: \(\frac{{AB}}{{AC}} = \frac{5}{6} \Rightarrow AB = \frac{5}{6}AC\) Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\)\( \Leftrightarrow \frac{1}{{{{30}^2}}} = \frac{{36}}{{25A{C^2}}} + \frac{1}{{A{C^2}}}\) \(\begin{array}{l} \Leftrightarrow \frac{1}{{{{30}^2}}} = \frac{{61}}{{25A{C^2}}} \Leftrightarrow A{C^2} = 2196 \Leftrightarrow AC = 6\sqrt {61} \,\,\,\left( {cm} \right)\\ \Rightarrow AB = \frac{5}{6}.6\sqrt {61} = 5\sqrt {61} \,\,\left( {cm} \right).\end{array}\) Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = 1525 + 2196 = 3721 \Rightarrow BC = 61\,\,\left( {cm} \right)\) Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \( \Rightarrow A{B^2} = BH.BC\)\( \Leftrightarrow {\left( {5\sqrt {61} } \right)^2} = 61.BH\,\, \Leftrightarrow BH = 25\,\,\,\left( {cm} \right)\) Ta có: \(CH = BC - BH = 61 - 25 = 36\,\,\,\left( {cm} \right).\) Chọn B. Câu hỏi 17 : Cho tam giác \(ABC\) vuông tại \(A\), kẻ đường cao \(AH\). Biết \(AH = 12cm,BH = 9cm\). Tính diện tích tam giác\(ABC\).
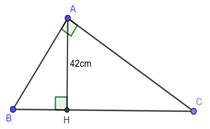
Đáp án: C Phương pháp giải: Sử dụng hệ thức lượng trong tam giác vuông để tính cạnh \(HC \Rightarrow BC.\) Khi đó ta có: \({S_{ABC}} = \frac{1}{2}AH.BC.\) Lời giải chi tiết: Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(A{H^2} = BH.CH\)\( \Leftrightarrow {12^2} = 9.C{H^2}\)\( \Leftrightarrow C{H^2} = 16\) \( \Leftrightarrow CH = 4\left( {cm} \right)\) Ta có: \(BC = BH + CH = 9 + 4 = 13\left( {cm} \right)\) \( \Rightarrow {S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}.12.13 = 78\,\,\,\left( {c{m^2}} \right)\) Chọn C. Câu hỏi 18 : Cho tam giác \(ABC\) vuông tại \(A\) . Biết \(\frac{{AB}}{{AC}} = \frac{3}{7}\), đường cao \(AH = 42cm\). Tính \(BH,HC\).
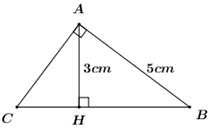
Đáp án: A Phương pháp giải: Áp dụng công thức hệ thức lượng trong tam giác vuông để tính cạnh \(AC:\,\,\,\,\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}.\) Kết hợp với giả thiết \(\frac{{AB}}{{AC}} = \frac{5}{6}\) để tính các cạnh \(AB,\,\,AC.\) Áp dụng công thức hệ thức lượng trong tam giác vuông để tính cạnh \(HB:\,\,\,A{B^2} = HB.BC \Rightarrow HC.\) Lời giải chi tiết: Ta có: \(\frac{{AB}}{{AC}} = \frac{3}{7} \Rightarrow AB = \frac{3}{7}AC\) Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(\begin{array}{l}\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Leftrightarrow \frac{1}{{{{42}^2}}} = \frac{{49}}{{9A{C^2}}} + \frac{1}{{A{C^2}}}\\ \Leftrightarrow \frac{1}{{{{42}^2}}} = \frac{{58}}{{9A{C^2}}} \Leftrightarrow A{C^2} = 11368\\ \Leftrightarrow AC = 14\sqrt {58} \,\,\left( {cm} \right)\\ \Rightarrow AB = \frac{3}{7}.14\sqrt {58} = 6\sqrt {58} \left( {cm} \right)\end{array}\) Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\) \(\begin{array}{l} \Leftrightarrow B{C^2} = {\left( {6\sqrt {58} } \right)^2} + {\left( {14\sqrt {58} } \right)^2}\\ \Leftrightarrow B{C^2} = 13456 \Rightarrow BC = 116\,\,\,\left( {cm} \right)\end{array}\) Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \( \Rightarrow A{B^2} = BH.BC\)\( \Leftrightarrow {\left( {6\sqrt {58} } \right)^2} = 116.BH \Leftrightarrow BH = 18\left( {cm} \right)\) \( \Rightarrow CH = BC - BH = 116 - 18 = 98\,\,\,\left( {cm} \right).\) Chọn A. Câu hỏi 19 : Trong hình vẽ bên, tam giác \(ABC\) vuông tại \(A,\) cạnh \(AB = 5cm,\) đường cao \(AH = 3cm.\) Độ dài cạnh \(BC\)bằng
Đáp án: C Phương pháp giải: - Áp dụng định lý Pytago trong tam giác vuông \(AHB\) tính \(BH\). - Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) tính \(BC\): \(A{B^2} = BH.BC\). Lời giải chi tiết: Áp dụng định lý Pytago trong tam giác vuông \(AHB\) ta có: \(\begin{array}{l}B{H^2} = A{B^2} - A{H^2}\\B{H^2} = {5^2} - {3^2}\\B{H^2} = 16\\ \Rightarrow BH = 4\,\,\left( {cm} \right)\end{array}\) Áp dụng hệ thức lượng trong tam giác vuông \(ABC\), đường cao \(AH\) ta có: \(A{B^2} = BH.BC\) \( \Rightarrow BC = \dfrac{{A{B^2}}}{{BH}} = \dfrac{{{5^2}}}{4} = \dfrac{{25}}{4}\,\,\left( {cm} \right)\). Chọn C. Câu hỏi 20 :
Đáp án: C Phương pháp giải: Lời giải chi tiết:
|