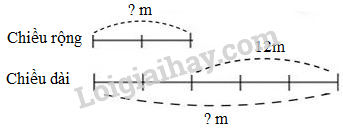
Đề số 4 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán lớp 4Tải vềĐáp án và lời giải chi tiết Đề số 4 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán lớp 4 Đề bài Phần 1. Trắc nghiệm (3 điểm) Khoanh vào chữ cái đặt trước câu trả lời đúng. Câu 1. Giá trị của chữ số 8 trong số 583624 là: A. 800 B. 8 000 C. 80 000 D. 800 000 Câu 2. Phân số \(\dfrac{2}{3}\) bằng phân số nào dưới đây A. \(\dfrac{20}{18}\) B. \(\dfrac{15}{45}\) C. \(\dfrac{5}{15}\) D. \(\dfrac{10}{15}\) Câu 3. Một hình bình hành có độ dài đáy bằng 16m; chiều cao bằng \(\dfrac{3}{4}\) độ dài đáy. Diện tích hình bình hành đó là: A. 12m2 B. 192m2 C. 96m2 D. 384m2 Câu 4. Giá trị biểu thức m - n × 4 với m = 180, n = 25 là A. 80 B. 100 C. 800 D. 1000 Câu 5. Trong một khu vườn, người ta để \(\dfrac{1}{3}\) diện tích trồng hoa, \(\dfrac{2}{5}\) diện tích trồng cây ăn quả. Diện tích còn lại ươm cây giống. Tìm phân số chỉ diện tích ươm cây giống. A. \(\dfrac{2}{15}\) B. \(\dfrac{11}{15}\) C. \(\dfrac{2}{3}\) D. \(\dfrac{4}{15}\) Câu 6. Một hình chữ nhật có chiều dài hơn chiều rộng 12m và chiều rộng bằng \(\dfrac{2}{5}\) chiều dài. Chu vi hình chữ nhật đó là: A. 28m B. 54m C. 56m D. 160m Phần 2. Tự luận (7 điểm) Bài 1. Đúng ghi Đ, sai ghi S. Hình bình hành ABCD (hình bên) có:
a) AB vuông góc với DC. b) AH vuông góc với DC. c) Chu vi hình bình hành ABCD là 18cm. d) Diện tích hình bình hành ABCD là 18cm2. Bài 2. Tìm \(x\) , biết: \(a)\; \dfrac{4}{5} \times x = \dfrac{1}{2}\). \(b) \; x:\dfrac{5}{8} = \dfrac{2}{{15}}\) Bài 3. Một căn phòng hình chữ nhật có tỉ số giữa chiều dài và chiều rộng là \(\dfrac{4}{3}\). Chiều dài hơn chiều rộng 2m. Người ta lát nền căn phòng đó bằng loại gạch vuông cạnh 2dm. Hỏi căn phòng đó lát hết bao nhiêu viên gạch? (Diện tích phần mạch vữa không đáng kể) Bài 4. Tính bằng cách thuận tiện \(a)\,\,\dfrac{22}{{13}} + \dfrac{7}{9} + \dfrac{2}{{9}} + \dfrac{4}{13}\) \(b)\,\,\dfrac{20}{21} \times \dfrac{{17}}{{15}} - \dfrac{{2}}{{15}} \times \dfrac{20}{21}\) Lời giải chi tiết Phần 1. Trắc nghiệm Câu 1. Phương pháp: Xác định hàng của chữ số , từ đó tìm được giá trị của chữ số đó. Cách giải: Chữ số 8 trong số 583624 thuộc hàng chục nghìn nên có giá trị là 80 000. Chọn C. Câu 2. Phương pháp: Áp dụng tính chất cơ bản của phân số: Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 ta được một phân số bằng phân số đã cho. Cách giải: Ta có: \(\dfrac{2}{3} = \dfrac{2 \times 5}{3\times 5} = \dfrac{10}{15}\) Chọn D. Câu 3. Phương pháp: - Tìm chiều cao ta lấy độ dài đáy nhân với \(\dfrac{3}{4}\). - Tính diện tích hình bình hành = độ dài đáy × chiều cao. Cách giải: Chiều cao hình bình hành là: 16 × \(\dfrac{3}{4}\) = 12 (m) Diện tích hình bình hành đó là: 16 × 12 = 192 (m2) Đáp số: 192m2. Chọn B. Câu 4. Phương pháp: Thay giá trị của m và n vào biểu thức đã cho rồi tính giá trị. Biểu thức có phép trừ và phép nhân thì thực hiện phép nhân trước, thực hiện phép trừ sau. Cách giải: Thay m = 180, n = 25 vào biểu thức m – n × 4 ta có: 180 – 25 × 4 = 180 – 100 = 80 Chọn A. Câu 5. Phương pháp: - Coi diện tích cả khu vườn là \(1\) đơn vị. - Phân số chỉ diện tích ươm cây trồng = \(1-\) phân số chỉ diện tích trồng hoa \(-\) phân số chỉ diện tích trồng cây ăn quả. Cách giải: Coi diện tích của cả khu vườn là \(1\) đơn vị. Phân số chỉ diện tích ươm cây trồng là: \(1 - \dfrac{1}{3} - \dfrac{2}{5} = \dfrac{4}{{15}}\) (khu vườn) Đáp số: \(\dfrac{4}{{15}}\) khu vườn. Chọn D. Câu 6. Phương pháp: - Tìm chiều dài, chiều rộng theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số đó. - Tính chu vi = (chiều dài + chiều rộng) \(\times \, 2\). Cách giải: Ta có sơ đồ: Theo sơ đồ, hiệu số phần bằng nhau là: 5 - 2 = 3 (phần) Chiều rộng hình chữ nhật là: 12 : 3 × 2 = 8 (m) Chiều dài hình chữ nhật là: 12 + 8 = 20 (m) Chu vi hình chữ nhật là: (20 + 8) × 2 = 56 (m) Chọn C. 56m Phần 2. Tự luận Bài 1. Phương pháp: - Muốn tính chu vi hình bình hành ta lấy tổng độ dài 2 cạnh liền nhau nhân với 2. - Tính diện tích hình bình hành ta lấy đọ dài đáy nhân với chiều cao Cách giải: Ta có: Chu vi hình bình hành ABCD là: (6 + 4) × 2 = 20 (cm) Diện tích hình bình hành ABCD là: 6 × 3 =18 (cm2) Vậy ta có kết quả như sau: a) AB vuông góc với DC (S) b) AH vuông góc với DC (Đ) c) Chu vi hình bình hành ABCD là 18cm (S) d) Diện tích hình bình hành ABCD là 18cm2 (Đ). Bài 2. Phương pháp: - Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết. - Muốn tìm số bị chia ta lấy thương nhân với số chia. Cách giải: a) \(\begin{array}{l}\dfrac{4}{5} \times x = \dfrac{1}{2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{1}{2}:\dfrac{4}{5}\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{{1 \times 5}}{{2 \times 4}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{5}{8}\end{array}\).
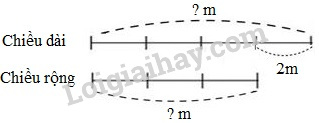
\(\begin{array}{l}x:\dfrac{5}{8} = \dfrac{2}{{15}}\\x\,\,\,\,\,\,\,\,\,\,\, = \dfrac{2}{{15}} \times \dfrac{5}{8}\\x\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{2 \times 5}}{{15 \times 8}}\\x\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{10}}{{120}} = \dfrac{1}{{12}}\end{array}\) Câu 7. Phương pháp: - Tìm chiều dài và chiều rộng căn phòng theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số đó. - Diện tích căn phòng = chiều dài \(\times\) chiều rộng. - Diện tích viên gạch = cạnh \(\times\) cạnh. - Số viên gạch cần dùng = diện tích căn phòng : diện tích viên gạch (chú ý hai diện tích phải cùng đơn vị đo). Cách giải: Ta có sơ đồ: Theo sơ đồ, hiệu số phần bằng nhau là: 4 - 3 = 1 (phần) Chiều dài căn phòng là: 2 : 1 × 4 = 8 (m) Chiều rộng căn phòng là: 8 - 2 = 6 (m) Diện tích căn phòng là: 8 × 6 = 48 (m2) 48m2 = 4800dm2 Diện tích viên gạch là: 2 × 2 = 4 (dm2) Số viên gạch cần lát là: 4800 : 4 = 1200 (viên gạch) Đáp số: 1200 viên gạch. Bài 4. a) Áp dụng tính chất giao hoán và kết hợp của phép cộng để nhóm hai phân số có cùng mẫu số lại với nhau. b) Áp dụng công thức: a × b – a × c = a × (b – c). Cách giải: \(\begin{array}{*{20}{l}}{a){\mkern 1mu} {\mkern 1mu} \dfrac{{22}}{{13}} + \dfrac{7}{9} + \dfrac{2}{9} + \dfrac{4}{{13}}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \left( {\dfrac{{22}}{{13}} + \dfrac{4}{{13}}} \right) + \left( {\dfrac{7}{9} + \dfrac{2}{9}} \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \dfrac{{26}}{{13}} + \dfrac{9}{9}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = 2 + 1 = 3}\end{array}\) \(\begin{array}{*{20}{l}}{b){\mkern 1mu} {\mkern 1mu} \dfrac{{20}}{{21}} \times \dfrac{{17}}{{15}} - \dfrac{2}{{15}} \times \dfrac{{20}}{{21}}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \dfrac{{20}}{{21}} \times \dfrac{{17}}{{15}} - \dfrac{{20}}{{21}} \times \dfrac{2}{{15}}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \dfrac{{20}}{{21}} \times \left( {\dfrac{{17}}{{15}} - \dfrac{2}{{15}}} \right)}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \dfrac{{20}}{{21}} \times \dfrac{{15}}{{15}}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \dfrac{{20}}{{21}} \times 1 = \dfrac{{20}}{{21}}}\end{array}\) HocTot.Nam.Name.Vn
|