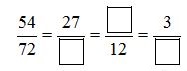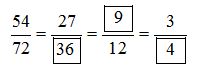Bài 1, 2, 3 trang 114 SGK Toán 4

Bài 1

Rút gọn các phân số : 

a) $\dfrac{4}{6}$ ; $\dfrac{12}{8}$; $\dfrac{15}{25}$;$\dfrac{11}{22}$ ; $\dfrac{36}{10}$ ; $\dfrac{75}{36}.$

b) $\dfrac{5}{10}$; $\dfrac{12}{36}$; $\dfrac{9}{72}$; $\dfrac{75}{300}$; $\dfrac{15}{35}$; $\dfrac{4}{100}.$

Phương pháp giải:

Cách rút gọn phân số:

- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn $1.$

- Chia tử số và mẫu số cho số đó.

Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).

Lời giải chi tiết:

a) $\dfrac{4}{6} = \dfrac{4 : 2}{6 : 2 } = \dfrac{2}{3}$                         $\dfrac{12}{8}=\dfrac{12 : 4}{8 : 4 } = \dfrac{3}{2}$

$\dfrac{15}{25} =\dfrac{15 : 5}{25 : 5 } = \dfrac{3}{5}$                         $\dfrac{11}{22} = \dfrac{11: 11}{22 : 11 } = \dfrac{1}{2}$

$\dfrac{36}{10} =\dfrac{36: 2}{10 : 2 } = \dfrac{18}{5}$                        $\dfrac{75}{36}= \dfrac{75: 3}{36 : 3 } = \dfrac{25}{12}$

b) $\dfrac{5}{10} = \dfrac{5: 5}{10 : 5} = \dfrac{1}{2}$                       $\dfrac{12}{36} = \dfrac{12: 12}{36 : 12} = \dfrac{1}{3}$

$\dfrac{9}{72}= \dfrac{9: 9}{72 : 9} = \dfrac{1}{8}$                           $\dfrac{75}{300} = \dfrac{75: 75}{300 : 75} = \dfrac{1}{4}$

 $\dfrac{15}{35}= \dfrac{15: 5}{35 : 5} = \dfrac{3}{7}$                          $\dfrac{4}{100} = \dfrac{4: 4}{100 : 4} = \dfrac{1}{25}$

Bài 2

Trong các phân số:  $\dfrac{1}{3};\;\dfrac{4}{7}; \; \dfrac{8}{12};\;  \dfrac{30}{36};\; \dfrac{72}{73}$ :

a) Phân số nào tối giản ? Vì sao?

b) Phân số nào rút gọn được? Hãy rút gọn phân số đó.

Phương pháp giải:

a) Phân số tối giản là phân số mà tử số và mẫu số không thể cùng chia hết cho một số tự nhiên nào lớn hơn 1 (hay phân số không thể rút gọn được nữa).

b) Cách rút gọn phân số :

- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn $1$.

- Chia tử số và mẫu số cho số đó.

Cứ làm như thế cho đến khi nhận được phân số tối giản.

Lời giải chi tiết:

a) Các phân số tối giản là : $\dfrac{1}{3};\dfrac{4}{7}; \dfrac{72}{73}$

Vì tử số và mẫu số của mỗi phân số trên không cùng chia hết cho một số tự nhiên nào khác $1$.

b) Các phân số rút gọn được là: $\dfrac{8}{12};\dfrac{30}{36}.$

$\dfrac{8}{12}= \dfrac{8 : 4}{12 : 4} = \dfrac{2}{3}$ ;                 $\dfrac{30}{36}= \dfrac{30 : 6}{36 : 6} = \dfrac{5}{6}$

Bài 3

Viết số thích hợp vào ô trống : 

Phương pháp giải:

Chia cả tử và mẫu của phân số đã cho với cùng một số rồi điền kết quả thích hợp vào ô trống.

Lời giải chi tiết:

Rút gọn các phân số ta có :

$\dfrac{54}{72} = \dfrac{54:2}{72:2} =\dfrac{27}{36}$;

$\dfrac{27}{36} = \dfrac{27:3}{36:3} =\dfrac{9}{12}$;

$\dfrac{9}{12} = \dfrac{9:3}{12:3} =\dfrac{3}{4}$.

Vậy ta có kết quả như sau : 

Lý thuyết

2. Rút gọn phân số

Có thể rút gọn phân số để được một phân số có tử số và mẫu số bé đi mà phân số mới vẫn bằng phân số đã cho.

Ví dụ 1: Rút gọn phân số: $\dfrac{6}{8}$ .

Ta thấy: $6$ và $8$ đều chia hết cho $2$ nên

$\dfrac{6}{8} = \dfrac{{6:2}}{{8:2}} = \dfrac{3}{4}$.

$3$ và $4$ không cùng chia hết cho một số tự nhiên nào lớn hơn $1$, nên phân số $\dfrac{3}{4}$ không thể rút gọn được nữa. Ta nói rằng: $\dfrac{3}{4}$ là phân số tối giản và phân số $\dfrac{6}{8}$ đã được rút gọn thành phân số tối giản $\dfrac{3}{4}$.

Ví dụ 2: Rút gọn phân số: $\dfrac{{18}}{{54}}$ .

Ta thấy: $18$ và $54$ đều chia hết cho $2$ nên

$\dfrac{{18}}{{54}} = \dfrac{{18:2}}{{54:2}} = \dfrac{9}{{27}}$.

$9$ và $27$ cùng chia hết cho $9$ nên

                                                $\dfrac{9}{{27}} = \dfrac{{9:9}}{{27:9}} = \dfrac{1}{3}$

$1$ và $3$ không cùng chia hết cho một số tự nhiên nào lớn hơn $1$, nên $\dfrac{1}{3}$ là phân số tối giản.

Vậy $\dfrac{{18}}{{54}} = \dfrac{1}{3}$.

Lưu ý: Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn $1$, hay phân số tối giản là phân số không thể rút gọn được nữa.