Bài 1, 2, 3, 4 trang 147 SGK Toán 4Bài 1: Viết tỉ số của a và b biết.
Lựa chọn câu để xem lời giải nhanh hơn
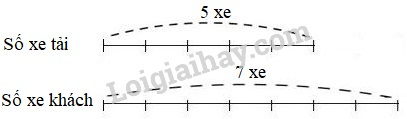
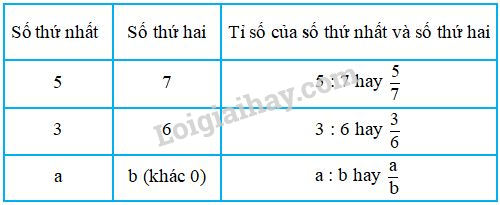
Bài 1 Video hướng dẫn giải Viết tỉ số của và biết: a) b) c) d) Phương pháp giải: Tỉ số của và là hay ( khác ). Lời giải chi tiết: a) Tỉ số của và là hay . b) Tỉ số của và là hay . c) Tỉ số của và là hay . d) Tỉ số của và là hay . Bài 2 Video hướng dẫn giải Trong hộp có bút đỏ và bút xanh. a) Viết tỉ số của số bút đỏ và số bút xanh; b) Viết tỉ số của số bút xanh và số bút đỏ. Phương pháp giải: Tỉ số của và là hay ( khác ). Lời giải chi tiết: a) Tỉ số của bút đỏ và bút xanh là: hay . b) Tỉ số của bút xanh và bút đỏ là: hay . Bài 3 Video hướng dẫn giải Trong một tổ có bạn trai và bạn gái. a) Viết tỉ số của số bạn trai và số bạn của cả tổ. b) Viết tỉ số của số bạn gái và số bạn của cả tổ. Phương pháp giải: Tỉ số của và là hay ( khác ). Lời giải chi tiết: Tổng số bạn của cả tổ là: (bạn) a) Tỉ số của số bạn trai và số bạn của cả tổ là: hay . b) Tỉ số của số bạn gái và số bạn của cả tổ là: hay . Bài 4 Video hướng dẫn giải Trên bãi cỏ có con bò và có số trâu bằng số bò. Hỏi trên bãi đó có mấy con trâu? Phương pháp giải: Để tìm số trâu ta đi tìm của con. Để tìm của con ta lấy nhân với , sau đó ghi thêm đơn vị vào kết quả. Lời giải chi tiết: Tóm tắt Bò: 20 con Trâu: số bò TRâu: ... con? Bài giải Số trâu ở trên bãi cỏ là: (con) Đáp số: con. Lý thuyết Ví dụ 1 : Một đội xe có xe tải và xe khách. Ta nói : - Tỉ số của số xe tải và số xe khách là hay . Tỉ số này cho biết số xe tải bằng số xe khách. - Tỉ số của số xe khách và số xe tải là hay . Tỉ số này cho biết số xe khách bằng số xe tải. Ví dụ 2: Ta nói rằng : Tỉ số của và là hay ( khác ).
>> Học trực tuyến các môn Toán, Tiếng Việt, Tiếng Anh lớp 4 trên Tuyensinh247.com. Cam kết giúp con lớp 4 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|