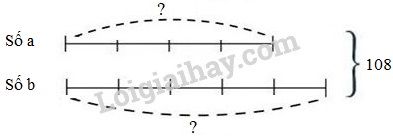
Đề số 8 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán lớp 4Đáp án và lời giải chi tiết Đề số 8 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán lớp 4 Đề bài Câu 1. Đúng ghi Đ, sai ghi S vào ô trống: Tìm \(a\) và \(b\) biết \(a + b = 108\,;\,\,\dfrac{a}{b} = \dfrac{4}{5}\).
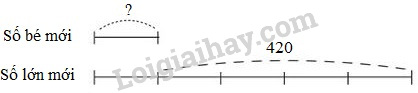
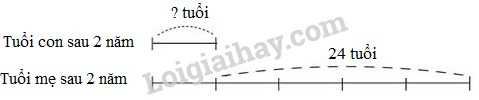
Câu 2. Khoanh vào chữ đặt trước câu trả lời đúng: Hiệu hai số là 420. Nếu cùng thêm vào mỗi số 30 thì số bé mới bằng \(\dfrac{1}{5}\) số lớn mới. Tìm hai số đã cho. A) 495 và 75 B) 105 và 525 C) 85 và 505 Câu 3. Đúng ghi Đ, sai ghi S vào ô trống: Mẹ hơn con 24 tuổi, biết rằng 2 năm nữa tuổi con bằng \(\dfrac{1}{5}\) tuổi mẹ. Tính tuổi con hiện nay.
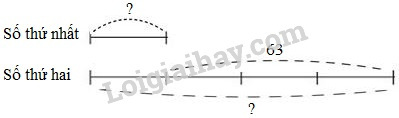
Câu 4. Khoanh vào chữ đặt trước câu trả lời đúng: Số thứ hai hơn số thứ nhất là 63. Nếu gấp số thứ nhất lên 4 lần thì được số thứ hai. Tìm hai số đó. A) 19 và 82 B) 20 và 83 C. 21 và 84 Câu 5. Đúng ghi Đ, sai ghi S vào ô trống: Tổng hai số là \(\dfrac{{17}}{2}\). Tỉ số của hai số là \(\dfrac{5}{{12}}\). Tìm hai số đó.
Câu 6. Đúng ghi Đ, sai ghi S vào ô trống: Tìm \(a,b\) biết: \(a - b = \dfrac{1}{2};\,\,\dfrac{b}{a} = \dfrac{1}{2}\)
Câu 7. Một mảnh vườn hình chữ nhật có chiều rộng bằng \(\dfrac{3}{5}\) chiều dài. Nếu chiều dài bớt đi \(12m\), chiều rộng thêm vào \(4m\) thì mảnh vườn trở thành hình vuông. Tính diện tích mảnh vườn đó. Lời giải chi tiết Câu 1. Phương pháp: Tìm \(a\) và \(b\) theo dạng toán tìm hai số khi biết tổng và tỉ số của hai số đó. Cách giải: Ta có sơ đồ: Tổng số phần bằng nhau là: \(4 + 5 = 9\) (phần) Số \(a\) là: \(108:9 \times 4 = 48\) Số \(b\) là: \(108 - 48 = 60\) Ta có bảng đáp án sau:
Câu 2. Phương pháp: - Nếu cùng thêm vào mỗi số 30 thì hiệu của hai số không thay đổi và bằng 420. - Tìm số bé mới và số lớn mới theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số đó. - Tìm số bé lúc đầu = số bé mới \(-30.\) - Số lớn lúc đầu = số bé lúc đầu \(+\) hiệu của hai số. Cách giải: Nếu cùng thêm vào mỗi số 30 thì hiệu của hai số không thay đổi và bằng 420. Ta có sơ đồ: Hiệu hai phần bằng nhau là: \(5 - 1 = 4\) (phần) Số bé mới là: \(420:4 \times 1 = 105\) Số bé lúc đầu là: \(105 - 30 = 75\) Số lớn lúc đầu là: \(420 + 75 = 495\) Chọn A. 495 và 75 Câu 3. Phương pháp: - Hiệu số tuổi không thay đổi theo thời gian. Mẹ hơn con 24 tuổi thì 2 năm nữa mẹ vẫn hơn con 24 tuổi. - Tìm tuổi con sau 2 năm nữa theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số. - Tìm tuổi con hiện nay = tuổi con sau 2 năm nữa \(-2\) tuổi. Cách giải: Hiệu số tuổi không thay đổi theo thời gian. Mẹ hơn con 24 tuổi thì 2 năm nữa mẹ vẫn hơn con 24 tuổi. Ta có sơ đồ: Hiệu số phần bằng nhau là: \(5 - 1 = 4\) (phần) Tuổi của con sau 2 năm là: \(24:4 \times 1 = 6\) (tuổi) Tuổi của con hiện tại là: \(6 - 2 = 4\) (tuổi) Ta có bảng sau:
Câu 4. Phương pháp: Nếu gấp số thứ nhất lên 4 lần thì được số thứ hai hay ta có số thứ hai gấp 4 lần số thứ nhất. Ta tìm hai số theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số. Cách giải: Nếu gấp số thứ nhất lên 4 lần thì được số thứ hai hay ta có số thứ hai gấp 4 lần số thứ nhất. Ta có sơ đồ: Hiệu hai phần bằng nhau là: \(4 - 1 = 3\) (phần) Số thứ nhất là: \(63:3 \times 1 = 21\) Số thứ hai là: \(21 + 63 = 84\) Chọn C. 21 và 84 Câu 5. Phương pháp: Ta tìm hai số theo dạng toán tìm hai số khi biết tổng và tỉ số của hai số. Cách giải: Tỉ số của hai số là \(\dfrac{5}{{12}}\) nên nếu coi số bé gồm \(5\) phần bằng nhau thì số lớn gồm \(12\) phần như thế. Tổng hai phần bằng nhau là: \(5 + 12 = 17\) (phần) Số thứ nhất là: \(\dfrac{{17}}{2}:17 \times 5 = \dfrac{5}{2}\) Số thứ hai là: \(\dfrac{{17}}{2} - \dfrac{5}{2} = \dfrac{{12}}{2} = 6\) Ta có bảng đáp án sau:
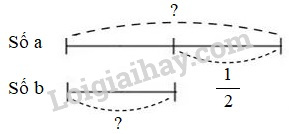
Câu 6. Phương pháp: Ta tìm hai số theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số. Cách giải: Ta có \(\dfrac{b}{a} = \dfrac{1}{2}\) nên tỉ số của hai số \(b\) và \(a\) là \(\dfrac{1}{2}\). Ta có sơ đồ: Hiệu hai phần bằng nhau là: \(2 - 1 = 1\) (phần) Số \(a\) là: \(\dfrac{1}{2}:1 \times 2 = 1\) Số \(b\) là: \(1 - \dfrac{1}{2} = \dfrac{1}{2}\) Ta có bảng đáp án sau:
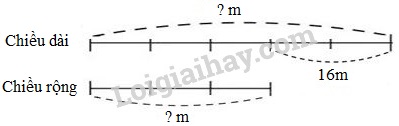
Câu 7. Phương pháp: - Tìm hiệu giữa chiều dài và chiều rộng: Vì chiều dài bớt đi \(12m\), chiều rộng thêm vào \(4m\) thì mảnh vườn trở thành hình vuông nên hiệu giữa chiều dài và chiều rộng là \(12 + 4 = 16m\). - Tìm chiều dài và chiều rộng theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số đó. - Tính diện tích = chiều dài \(\times \) chiều rộng. Cách giải: Chiều dài hơn chiều rộng số mét là: \(12 + 4 = 16\;(m)\) Ta có sơ đồ: Hiệu số phần bằng nhau là: \(5 - 3 = 2\) (phần) Chiều rộng mảnh vườn là: \(16:2 \times 3 = 24\;(m)\) Chiều dài mảnh vườn là: \(24 + 16 = 40\;(m)\) Diện tích mảnh vườn là: \(40 \times 24 = 960\;(m^2)\) Đáp số: \(960m^2\). HocTot.Nam.Name.Vn
|