Đề số 1 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán lớp 4Tải vềĐáp án và lời giải chi tiết Đề số 1 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán lớp 4 Đề bài Phần 1. Trắc nghiệm (3 điểm) Khoanh vào chữ đặt trước câu trả lời đúng Câu 1. Các số: 20 000; 14 075; 19 999; 30 009; 19 070 được xếp theo thứ tự từ lớn đến bé là: A. 20 000; 30 009; 19 999; 19 070; 14 075 B. 30 009; 20 000; 19 999; 19 070; 14 075 C. 30 009; 19 999; 20 000; 19 070; 14 075 D. 14 075; 19 070; 19 999; 20 000; 30 009 Câu 2. Phân số lớn nhất trong các phân số \(\dfrac{3}{4};\dfrac{{100}}{{100}};\dfrac{{11}}{{12}};\dfrac{5}{3}\) là: A. \(\dfrac{3}{4}\) B. \(\dfrac{{100}}{{100}}\) C. \(\dfrac{{11}}{{12}}\) D. \(\dfrac{5}{3}\) Câu 3. Trong các số 4700; 61 059; 50 280; 6915 số chia hết cho 2, cho 3 và cho 5 là: A. 4700 B. 61 059 C. 50 280 D. 6915 Câu 4. Số thích hợp viết vào chỗ chấm để 57m2 3cm2 = ………cm2 là : A. 5730 B. 573 C. 5703 D. 570003 Câu 5. Một hình bình hành có độ dài đáy là 18cm, chiều cao bằng \(\dfrac{2}{3}\) độ dài đáy. Diện tích hình bình hành đó là: A. 108cm2 B. 216cm2 C. 243cm2 D. 486cm2 Câu 6. Một trường học có 945 học sinh nữ và chiếm \(\dfrac{7}{{15}}\) tổng số học sinh toàn trường. Hỏi trường đó có bao nhiêu học sinh nam? A. 1080 học sinh B. 1020 học sinh C. 980 học sinh D. 2025 học sinh Phần 2. Tự luận (7 điểm) Bài 1. (2 điểm)
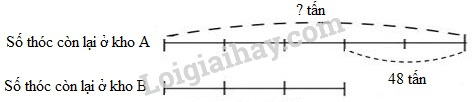
a) Đặt tính rồi tính 45093 + 83069 37978 – 5169 b) Tính: \(\dfrac{1}{3} + \dfrac{2}{5}\) \(\dfrac{6}{{11}}:\dfrac{3}{4}\) Bài 2. (1 điểm)Tìm \(x\): \(a)\,\,\dfrac{5}{6} - x = \dfrac{2}{3}\) \(b)\,\,x:\dfrac{2}{5} = \dfrac{7}{3}\) Bài 3. (3 điểm) Kho A có số thóc nhiều hơn kho B là 48 tấn. Sau khi mỗi kho lấy ra 24 tấn thì số thóc còn lại ở kho A bằng \(\dfrac{5}{3}\) số thóc còn lại ở kho B. Tính số thóc lúc đầu ở mỗi kho. Bài 4. (1 điểm) Tính bằng cách thuận tiện \(a)\,\,\dfrac{6}{{11}} + \dfrac{3}{7} + \dfrac{5}{{11}} + \dfrac{4}{7}\) \(b)\,\,\dfrac{5}{8} \times \dfrac{{11}}{{25}} + \dfrac{{14}}{{25}} \times \dfrac{5}{8}\) Lời giải chi tiết Phần 1. Trắc nghiệm Câu 1. Phương pháp: So sánh các số đã cho rồi sắp xếp các số đó theo thứ tự từ lớn đến bé. Cách giải: Ta có: 30 009 > 20 000 > 19 999 > 19 070 > 14 075. Vậy các số đã cho được sắp xếp theo thứ tự từ lớn đến bé là: 30 009; 20 000; 19 999; 19 070; 14 075. Chọn B. Câu 2. Phương pháp: Áp dụng cách so sánh phân số đã cho với 1: - Phân số có tử số lớn hơn mẫu số thì lớn hơn 1. - Phân số có tử số nhỏ hơn mẫu số thì nhỏ hơn 1. - Phân số có tử số bằng mẫu số thì bằng 1. Cách giải: Ta có: \(\dfrac{3}{4}<1\,;\;\;\dfrac{{100}}{{100}}=1\,;\;\;\dfrac{{11}}{{12}}<1;\) \(\dfrac{5}{3}>1\). Vậy phân số lớn nhất trong các phân số đã cho là \(\dfrac{5}{3}\). Chọn D. Câu 3. Phương pháp: - Các số có chữ số tận cùng là 0 thì chia hết cho cả 2 và 5. - Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3. Cách giải: Trong các số 4700; 61 059; 50 280; 6915, số chia hết cho 2 và cho 5 là: 4700 và 50 280. Số 4700 có tổng các chữ số là 4 + 7 + 0 + 0 = 11, vì 11 không chia hết cho 3 nên số 4700 không chia hết cho 3. Số 50 280 có tổng các chữ số là 5 + 0 + 2 + 8 + 0 = 15, vì 15 chia hết cho 3 nên số 50 280 chia hết cho 3. Vậy trong các số đã cho, số chia hết cho 2, cho 3 và cho 5 là 50 280. Chọn C. Câu 4. Phương pháp: Áp dụng kiến thức : 1m2 = 10000cm2 . Cách giải: Ta có 1m2 = 10000cm2 nên 57m2 = 570000cm2 . Do đó 57m2 3cm2 = 570000cm2 + 3cm2 = 570003cm2. Chọn D. Câu 5. Phương pháp: - Tính chiều cao ta lấy độ dài đáy nhân với \(\dfrac{2}{3}\). - Tính diện tích hình bình hành ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo). Cách giải: Chiều cao của hình bình hành đó là: 18 × \(\dfrac{2}{3}\) = 12 (cm) Diện tích của hình bình hành đó là: 18 × 12 = 216 (cm2) Đáp số: 216cm2. Chọn B. Câu 6. Phương pháp: - Tìm số học sinh toàn trường ta lấy số học sinh nữ chia cho 7 rồi nhân với 15 hoặc lấy số học sinh nữ chia cho \(\dfrac{7}{{15}}\). - Tìm số học sinh nam ta lấy số học sinh cả trường trừ đi số học sinh nữ. Cách giải: Số học sinh cả trường là: 945 : 7 × 15 = 2025 (học sinh) Số học sinh nam của trường đó là: 2025 - 945 = 1080 (học sinh) Đáp số: 1080 học sinh. Chọn A. Phần 2. Tự luận Bài 1. Phương pháp: a) Đặt tính sao cho các chữ số ở cùng hàng đặt thẳng cột với nhau, sau đó tính theo thứ tự từ phải sang trái. b) Muốn cộng hai phân số ta quy đồng mẫu số hai phân số rồi cộng hai phân số đó. Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược. Cách giải: a) \(\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{45093}\\{83069}\end{array}}\\\hline{128162}\end{array}\) \(\begin{array}{*{20}{c}}{ - \begin{array}{*{20}{c}}{37978}\\{\,\,\,5169}\end{array}}\\\hline{\,\,\,\,32809}\end{array}\) b) \(\dfrac{1}{3} + \dfrac{2}{5} = \dfrac{5}{{15}} + \dfrac{6}{{15}} = \dfrac{{11}}{{15}}\) \(\dfrac{6}{{11}}:\dfrac{3}{4} = \dfrac{6}{{11}} \times \dfrac{4}{3} = \dfrac{{24}}{{33}} = \dfrac{8}{{11}}\) Bài 2. Phương pháp: a) \(x\) là số trừ, muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu. b) \(x\) là số số bị chia, muốn tìm số bị chia ta lấy thương nhân với số chia. Cách giải: \(\begin{array}{l}a)\,\,\dfrac{5}{6} - x = \dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{5}{6} - \dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{1}{6}\end{array}\) \(\begin{array}{l}b)\,\,x:\dfrac{2}{5} = \dfrac{7}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{7}{3} \times \dfrac{2}{5}\\\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{{14}}{{15}}\end{array}\) Bài 3. Phương pháp: - Sau khi lấy mỗi kho ra 24 tấn thóc thì hiệu số thóc hai kho không đổi và bằng 48 tấn. - Ta tìm số thóc còn lại của mỗi kho theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số đó. - Tìm số thóc ban đầu ta lấy số thóc còn lại cộng với số thóc đã lấy ra. Cách giải: Sau khi lấy mỗi kho ra 24 tấn thóc thì hiệu số thóc hai kho không đổi và bằng 48 tấn. Ta có sơ đồ:
Hiệu số phần bằng nhau là: 5 - 3 = 2 (phần) Kho A sau khi lấy đi 24 tấn còn số thóc là: 48 : 2 × 5 = 120 (tấn) Kho A lúc đầu có số thóc là: 120 + 24 = 144 (tấn) Kho B lúc đầu có số thóc là: 144 - 48 = 96 (tấn) Đáp số: Kho A: 144 tấn; Kho B: 96 tấn. Bài 4. Phương pháp: a) Áp dụng tính chất giao hoán và kết hợp của phép cộng để nhóm hai phân số có cùng mẫu số lại với nhau. b) Áp dụng công thức: a × b + a × c = a × (b + c). Cách giải: \(\begin{array}{l}a)\,\,\dfrac{6}{{11}} + \dfrac{3}{7} + \dfrac{5}{{11}} + \dfrac{4}{7}\\\,\,\,\,\, = \left( {\dfrac{6}{{11}} + \dfrac{5}{{11}}} \right) + \left( {\dfrac{3}{7} + \dfrac{4}{7}} \right)\\\,\,\,\,\, = \dfrac{{11}}{{11}} + \dfrac{7}{7}\\\,\,\,\,\, = 1 + 1 = 2\end{array}\) \(\begin{array}{l}b)\,\,\dfrac{5}{8} \times \dfrac{{11}}{{25}} + \dfrac{{14}}{{25}} \times \dfrac{5}{8}\\\,\,\,\, = \dfrac{5}{8} \times \dfrac{{11}}{{25}} + \dfrac{5}{8} \times \dfrac{{14}}{{25}}\\\,\,\,\, = \dfrac{5}{8} \times \left( {\dfrac{{11}}{{25}} + \dfrac{{14}}{{25}}} \right)\\\,\,\,\, = \dfrac{5}{8} \times \dfrac{{25}}{{25}}\\\,\,\,\, = \dfrac{5}{8} \times 1 = \dfrac{5}{8}\end{array}\) HocTot.Nam.Name.Vn
|