Trắc nghiệm Bài 7: Hình vuông Toán 8 Cánh diềuĐề bài
Câu 1 :
Các dấu hiệu nhận biết sau, dấu hiệu nào không đủ để kết luận một hình vuông?
Câu 2 :
Khẳng định nào sau đây không là tính chất của hình vuông?
Câu 3 :
Định nghĩa đúng về hình vuông:
Câu 4 :
Hình vuông có bao nhiêu trục đối xứng?
Câu 5 :
Tứ giác nào sau đây vừa là hình chữ nhật, vừa là hình thoi?
Câu 6 :
Để chứng minh tứ giác ABCD là hình vuông, dấu hiệu nào sau đây là sai
Câu 7 :
Một hình vuông có độ dài đường chéo là 6cm. Độ dài cạnh hình vuông đó là
Câu 8 :
Một hình vuông có cạnh là 2dm. Độ dài đường chéo của hình vuông đó là:
Câu 9 :
Một hình vuông có chu vi là 32 cm. Hỏi diện tích hình vuông nhận giá trị nào sau đây?
Câu 10 :
Một hình vuông có diện tích là 25\(c{m^2}\). Hỏi chu vi hình vuông nhận giá trị nào sau đây?
Câu 13 :
Chọn câu sai. Tứ giác nào có hai đường chéo bằng nhau.
Câu 14 :
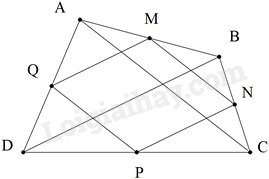
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA và MN // AC, NP // BD; \(MN = \frac{1}{2}AC,NP = \frac{1}{2}BD\). Hai đường chéo AC và BD cần thỏa mãn điều kiện gì để tứ giác MNPQ là hình vuông?
Câu 15 :
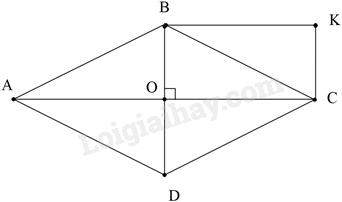
Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo. Qua Bvẽ đường thẳng song song với AC, qua C vẽ đường thẳng song song với BD, hai đường thẳng này cắt nhau ở K. Hình thoi ABCD Cần thỏa mãn điều kiện gì để tứ giác BOCK là hình vuông?
Câu 16 :
Cho hình vuông ABCD. Trên cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
Câu 17 :
Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của AB, CD; EF // AD //BC. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.Tứ giác EMFN là hình gì?
Câu 18 :
ho hình vuông ABCD. M là điểm nằm trong hình vuông. Gọi E, F lần lượt là hình chiếu của M trên cạnh AB và AD. Tứ giác AEMF là hình vuông khi.
Câu 19 :
Cho hình vuông ABCD cạnh 8 cm. M, N, P, Q là trung điểm các cạnh AB, BC, CD, DA. Tính diện tích tứ giác MNPQ.
Câu 20 :
Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là các trung điểm của AB, BC, AC và \(AM = \frac{1}{2}AB{;^{}}AP = \frac{1}{2}AC\). Tam giác ABC cần có thêm điều kiện gì để hình chữ nhật AMNP là hình vuông?
Câu 21 :
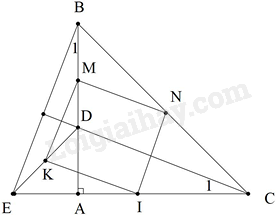
Tam giác ABC vuông tại A. Trên các cạnh AB ,AC lấy các điểm D, E sao cho BD = CE. Gọi I, K, M, N theo thứ tự là các điểm thuộc các cạnh DE, BE, CB, CD sao cho \(IK = MN = \frac{1}{2}BD,KM = IN = \frac{1}{2}CE\); IK // BD, IN //CE. Tứ giác IKMN là hình gì?
Câu 22 :
Cho tam giác ABC vuông cân tại A, điểm D thuộc cạnh AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AD. Gọi M, N, I, K theo thứ tự là các điểm thuộc các cạnh BD, BC, EC, ED sao cho \(MN//CD,MN = \frac{1}{2}CD;KI//CD,KI = \frac{1}{2}CD;NI//BE,NI = \frac{1}{2}BE;MK//BE,MK = \frac{1}{2}BE\).Tứ giác MNIK là hình gì?
Lời giải và đáp án
Câu 1 :
Các dấu hiệu nhận biết sau, dấu hiệu nào không đủ để kết luận một hình vuông?
Đáp án : D Phương pháp giải :
Dựa vào dấu hiệu nhận biết của hình vuông
Lời giải chi tiết :
Câu A, B, C là các câu đúng theo dấu hiệu nhận biết hình vuông. Câu D sai vì hình thoi có hai đường chéo vuông góc, hình thoi có hai đường chéo bằng nhau là hình vuông.
Câu 2 :
Khẳng định nào sau đây không là tính chất của hình vuông?
Đáp án : C Phương pháp giải :
Dựa vào tính chất của hình vuông
Lời giải chi tiết :
Câu A, B, D là các câu đúng theo tính chất hình vuông. Câu C sai vì Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau là định nghĩa hình vuông.
Câu 3 :
Định nghĩa đúng về hình vuông:
Đáp án : D Phương pháp giải :
Dựa vào định nghĩa của hình vuông
Lời giải chi tiết :
Theo định nghĩa hình vuông ta có: Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
Câu 4 :
Hình vuông có bao nhiêu trục đối xứng?
Đáp án : D Phương pháp giải :
Dựa vào tính chất của hình vuông
Lời giải chi tiết :
Hình vuông có 4 trục đối xứng.
Câu 5 :
Tứ giác nào sau đây vừa là hình chữ nhật, vừa là hình thoi?
Đáp án : B Phương pháp giải :
Dựa vào tính chất của hình vuông
Lời giải chi tiết :
Vì theo tính chất hình vuông ta có: Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
Câu 6 :
Để chứng minh tứ giác ABCD là hình vuông, dấu hiệu nào sau đây là sai
Đáp án : C Phương pháp giải :
Dựa vào dấu hiệu nhận biết của hình vuông
Lời giải chi tiết :
Tứ giác ABCD hình thoi có hai đường chéo AC, BD vuông góc với nhau nhưng chưa thể kết luận được ABCD là hình vuông.
Câu 7 :
Một hình vuông có độ dài đường chéo là 6cm. Độ dài cạnh hình vuông đó là
Đáp án : A Phương pháp giải :
Áp dụng định lí Pytago
Lời giải chi tiết :
Gọi cạnh của hình vuông là \(x,x > 0\). Áp dụng định lí Pytago ta có: \({x^2} + {x^2} = {6^2} \Leftrightarrow 2{x^2} = 36 \Leftrightarrow x = \sqrt {18} \)
Câu 8 :
Một hình vuông có cạnh là 2dm. Độ dài đường chéo của hình vuông đó là:
Đáp án : B Phương pháp giải :
Áp dụng định lí Pytago
Lời giải chi tiết :
Gọi độ dài đường chéo của hình vuông là \(x,x > 0\). Áp dụng định lí Pytago ta có: \({2^2} + {2^2} = {x^2} \\ {x^2} = 8 \\ x = 2\sqrt 2 \)
Câu 9 :
Một hình vuông có chu vi là 32 cm. Hỏi diện tích hình vuông nhận giá trị nào sau đây?
Đáp án : B Phương pháp giải :
Tính độ dài một cạnh của hình vuông rồi tính diện tích của hình vuông.
Lời giải chi tiết :
Cạnh của hình vuông là: 32 : 4 = 8 (\(c{m^2}\)) Diện tích của hình vuông là: 8 . 8 = 64 (\(c{m^2}\))
Câu 10 :
Một hình vuông có diện tích là 25\(c{m^2}\). Hỏi chu vi hình vuông nhận giá trị nào sau đây?
Đáp án : C Phương pháp giải :
Tính cạnh của hình vuông rồi tính diện tích của hình vuông đó.
Lời giải chi tiết :
Cạnh của hình vuông là: 25 : 5 = 5 (cm)
Chu vi của hình vuông là: 5.4 = 20 (cm)
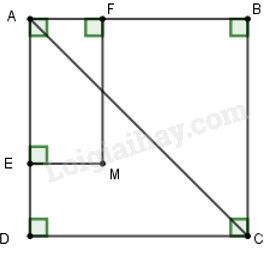
Đáp án : D Phương pháp giải :
Dựa vào dấu hiệu của hình vuông.
Lời giải chi tiết :
Từ hình vẽ ta thấy hai đường chéo của tứ giác vuông góc và giao nhau tại trung điểm mỗi đường nên nó là hình thoi. Hình thoi này có hai đường chéo bằng nhau nên nó là hình vuông
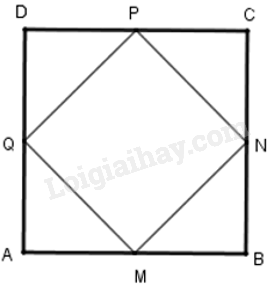
Đáp án : A Phương pháp giải :
Dựa vào dấu hiệu nhận biết của hình vuông
Lời giải chi tiết :
Từ hình vẽ ta thấy bốn cạnh của tứ giác này bằng nhau nên tứ giác này là hình thoi. Hình thoi này có một góc vuông nên nó là hình vuông.
Câu 13 :
Chọn câu sai. Tứ giác nào có hai đường chéo bằng nhau.
Đáp án : D Phương pháp giải :
Dựa vào tính chất của hình thoi, hình thang cân, hình chữ nhật, hình vuông.
Lời giải chi tiết :
Trong các hình: hình vuông, hình chữ nhật, hình thang cân, hình thoi thì hình thoi là hình có hai đường chéo không bằng nhau.
Câu 14 :
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA và MN // AC, NP // BD; \(MN = \frac{1}{2}AC,NP = \frac{1}{2}BD\). Hai đường chéo AC và BD cần thỏa mãn điều kiện gì để tứ giác MNPQ là hình vuông?
Đáp án : B Phương pháp giải :
Chứng minh MNPQ là hình bình hành có hai đường chéo bằng nhau và vuông góc với nhau.
Lời giải chi tiết :
Tứ giác MNPQ có hai cạnh đối vừa song song vừa bằng nhau nên tứ giác MNPQ là hình bình hành. Để hình bình hành MNPQ là hình vuông thì \(\left\{ \begin{array}{l}MN \bot NP\\MN = NP\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}AC \bot BD\\AC = BD\end{array} \right.\) Vì MN // AC, NP // BD nên \(AC \bot BD\) Lại có: \(MN = \frac{1}{2}AC,NP = \frac{1}{2}BD\) nên AC = BD Vậy để tứ giác MNPQ là hình vuông thì hai đường chéo AC và BD bằng nhau và vuông góc với nhau. Hình bình hành có hai đường chéo bằng nhau và vuông góc với nhau.
Câu 15 :
Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo. Qua Bvẽ đường thẳng song song với AC, qua C vẽ đường thẳng song song với BD, hai đường thẳng này cắt nhau ở K. Hình thoi ABCD Cần thỏa mãn điều kiện gì để tứ giác BOCK là hình vuông?
Đáp án : A Phương pháp giải :
Dựa vào dấu hiệu nhận biết của hình vuông
Lời giải chi tiết :
Tứ giác BOCK có các cạnh đối song song nên tứ giác BOCK là hình bình hành. Lại có: \(\widehat {BOC} = {90^0}\)(hai đường chéo của hình thoi vuông góc với nhau tại O) \( \Rightarrow \)Tứ giác BOCK là hình chữ nhật. Để hình chữ nhật BOCK là hình vuông thì BO = OC \( \Rightarrow \)BD =AC \( \Rightarrow \)Hình thoi ABCD là hình vuông.
Câu 16 :
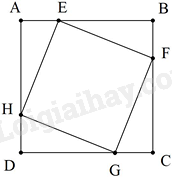
Cho hình vuông ABCD. Trên cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
Đáp án : D Phương pháp giải :
Chứng minh tứ giác EFGH là hình thoi có một góc là góc vuông
Lời giải chi tiết :
Ta có: AH = BE = CF = DG \( \Rightarrow \Delta AEH = \Delta BFE = \Delta CGF = \Delta DHG(c.g.c)\) Do đó: EH = FE = GF = HG (1) Lại có:\(\Delta AEH = \Delta BFE \Rightarrow \widehat {{\rm{BEF}}} = \widehat {AHE}\) \(\begin{array}{l} \Rightarrow \widehat {AEH} + \widehat {{\rm{BEF}}} = {90^0}\\ \Rightarrow \widehat {FEH} = {90^0}(2)\end{array}\) Từ (1) và (2) suy ra tứ giác EFGH là hình vuông. Hình thoi có một góc vuông là hình vuông.
Câu 17 :
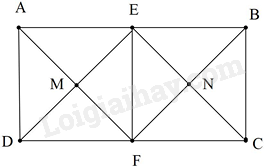
Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của AB, CD; EF // AD //BC. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.Tứ giác EMFN là hình gì?
Đáp án : D Phương pháp giải :
Chứng minh tứ giác EMFN là hình chữ nhật có bố cạnh bằng nhau nên tứ giác EMFN là hình vuông.
Lời giải chi tiết :
Vì EF // AD //BC Và AE = FB = BC = CF = FD = DA Lại có: AE // DF \( \Rightarrow \)Tứ giác ADFE là hình bình hành (dhnb) Lại có: \(\widehat A = {90^0}\)( ABCD là hình chữ nhật) \( \Rightarrow \)Tứ giác ADFE là hình chữ nhật. Mặt khác: \(AD = AE = \frac{1}{2}AB\) \( \Rightarrow \) ADFE là hình vuông. Chứng minh tương tự ta có BCFE là hình vuông Do đó \(\Delta MEF\) và \(\Delta N{\rm{EF}}\) là hai tam giác vuông cân tại M, N Suy ra tứ giác EMFN là hình vuông.
Câu 18 :
ho hình vuông ABCD. M là điểm nằm trong hình vuông. Gọi E, F lần lượt là hình chiếu của M trên cạnh AB và AD. Tứ giác AEMF là hình vuông khi.
Đáp án : A Phương pháp giải :
Dựa vào dấu hiệu của hình vuông
Lời giải chi tiết :
Tứ giác AFME có: \(\widehat A = \widehat {AFM} = \widehat {A{\rm{E}}M} = {90^o}\) nên AEMF là hình chữ nhật Để hình chữ nhật AEMF là hình vuông thì AM là phân giác của góc \(\widehat {EAF}\) Mà ta lại có: AC là phân giác \(\widehat {DAB}\) (do ABCD là hình vuông) Nên suy ra M \( \in \) AC.
Câu 19 :
Cho hình vuông ABCD cạnh 8 cm. M, N, P, Q là trung điểm các cạnh AB, BC, CD, DA. Tính diện tích tứ giác MNPQ.
Đáp án : D Phương pháp giải :
Áp dụng: SMNPQ = SABCD – SAMQ – SMBN – SCPN – SDPQ
Lời giải chi tiết :
Vì ABCD là hình vuông và M, N, P, Q là trung điểm các cạnh AB, BC, CD, CA nên ta có AM = MB = BN = NC = CP = PD = DQ = QA = \(\frac{1}{2}\)AB = 4 cm Từ đó: ΔAQM = ΔBMN = ΔCPN = ΔDQP (c – g – c) Suy ra \({S_{QAM}} = {S_{MNB}} = {S_{CPN}} = {S_{DPQ}} = \frac{{DQ.DP}}{2} = \frac{{{8^2}}}{8} = 8\) Lại có SABCD = 82 = 64. Nên SMNPQ = SABCD – SAMQ – SMBN – SCPN – SDPQ = \({8^2} - 4.\frac{{{8^2}}}{8} = \frac{1}{2}{.8^2} = 32\) Vậy SMNPQ = 32 cm2.
Câu 20 :
Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là các trung điểm của AB, BC, AC và \(AM = \frac{1}{2}AB{;^{}}AP = \frac{1}{2}AC\). Tam giác ABC cần có thêm điều kiện gì để hình chữ nhật AMNP là hình vuông?
Đáp án : B Phương pháp giải :
Dựa vào dấu hiệu nhận biết của hình vuông
Lời giải chi tiết :
Hình chữ nhật AMNP là hình vuông ⇔ AM = AP Vì: \(AM = \frac{1}{2}AB{;^{}}AP = \frac{1}{2}AC(gt)\) nên AM = AP ⇔ AB = AC Vậy nếu tam giác ABC vuông cân tại A thì hình chữ nhật AMNP là hình vuông.
Câu 21 :
Tam giác ABC vuông tại A. Trên các cạnh AB ,AC lấy các điểm D, E sao cho BD = CE. Gọi I, K, M, N theo thứ tự là các điểm thuộc các cạnh DE, BE, CB, CD sao cho \(IK = MN = \frac{1}{2}BD,KM = IN = \frac{1}{2}CE\); IK // BD, IN //CE. Tứ giác IKMN là hình gì?
Đáp án : A Phương pháp giải :
Dựa vào các dấu hiệu của hình vuông để chứng minh tứ giác IKMN là hình vuông.
Lời giải chi tiết :
Ta có: \(IK = MN = \frac{1}{2}BD,KM = IN = \frac{1}{2}CE\) Mà BD = CE nên IK = KM = MN = IN (1) Lại có: IK // BD, IN //CE Mặt khác: \(BD \bot CE\) \( \Rightarrow IK \bot IN(2)\) Từ (1) và (2) suy ra IKMN là hình vuông.
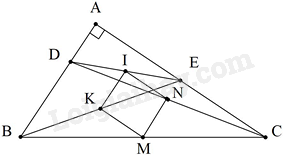
Câu 22 :
Cho tam giác ABC vuông cân tại A, điểm D thuộc cạnh AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AD. Gọi M, N, I, K theo thứ tự là các điểm thuộc các cạnh BD, BC, EC, ED sao cho \(MN//CD,MN = \frac{1}{2}CD;KI//CD,KI = \frac{1}{2}CD;NI//BE,NI = \frac{1}{2}BE;MK//BE,MK = \frac{1}{2}BE\).Tứ giác MNIK là hình gì?
Đáp án : C Phương pháp giải :
Chứng minh tứ giác MNIK có MN = NI = KI = MK và \(MN \bot MK\)
Do đó tứ giác MNIK là hình vuông. Lời giải chi tiết :
Ta có: \(\Delta ACD = \Delta ABE(c.g.c)\) Suy ra: CD = BE Lại có: \(\widehat {{C_1}} = \widehat {{B_1}}\) Mặt khác: \(\widehat {{B_1}}\) phụ với \(\widehat {BEC}\) nên \(\widehat {{C_1}}\) phụ với \(\widehat {BEC}\) Do đó: \(CD \bot BE\) Theo đề bài ta có: \(\begin{array}{l}MN//CD,MN = \frac{1}{2}CD\\KI//CD,KI = \frac{1}{2}CD\\NI//BE,NI = \frac{1}{2}BE\\MK//BE,MK = \frac{1}{2}BE\end{array}\) Từ đó suy ra MN = NI = KI = MK và \(MN \bot MK\) Do đó tứ giác MNIK là hình vuông.
|