Trắc nghiệm Bài 6: Hình thoi Toán 8 Cánh diềuĐề bài
Câu 1 :
Hãy chọn câu sai.
Câu 2 :
Điền từ thích hợp vào chỗ trống: “Tứ giác có hai đường chéo … là hình thoi”.
Câu 3 :
Hình thoi không có tính chất nào dưới đây?
Câu 4 :
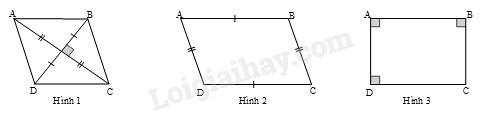
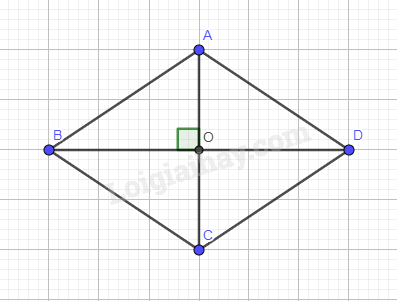
Trong các hình sau, hình nào vừa có tâm đối xứng, vừa có trục đối xứng?
Câu 6 :
Chọn câu trả lời sai.
Câu 7 :
Hình thoi có chu vi là 32 cm, cạnh hình thoi có độ dài là
Câu 9 :
Hình thoi có độ dài hai đường chéo là 24cm và 10cm thì cạnh của hình thoi đó bằng
Câu 10 :
Cho hình thoi ABCD có chu vi bằng 16 cm, đường cao bằng 2 cm. Tính các góc của hình thoi (\(\widehat A > \widehat B\)). Hãy chọn câu trả lời đúng.
Câu 11 :
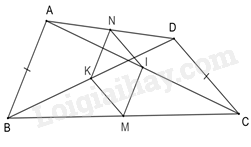
Tứ giác ABCD có AB = CD. Gọi M, N theo thứ tự là trung điểm của BC, DA. Gọi I, K theo thứ tự là trung điểm của AC và BD và\(MK = \frac{1}{2}CD;IM = \frac{1}{2}AB;NI = \frac{1}{2}CD;KN = \frac{1}{2}AB\). Tứ giác KMIN là hình gì?
Câu 12 :
Các phương án sau, phương án nào sai?
Câu 13 :
Hai đường chéo của hình thoi có độ dài lần lượt là 8cm và 10cm. Diện tích của hình thoi đó là ?
Câu 14 :
Một hình thoi có diện tích là \(\frac{5}{3}d{m^2}\). Biết độ dài một đường chéo bằng \(\frac{{25}}{2}dm\). Tính độ dài đường chéo còn lại.
Câu 15 :
Cho hình thoi ABCD có O là giao điểm hai đường chéo, biết AC = 16cm và OB = 6cm. Tính CD?
Câu 16 :
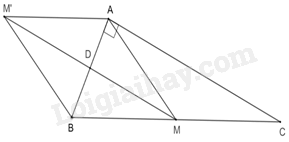
Cho tam giác ABC vuông ở A, trung tuyến AM. Gọi D là trung điểm của AB và MD // AC, \({M'}\) là điểm đối xứng với M qua D. Tứ giác \(AMBM'\) là hình gì?
Câu 17 :
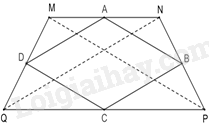
Cho hình thang cân MNPQ. Gọi A, B, C, D lần lượt là các điểm thuộc các cạnh MN, NP, PQ, QM và \(AD = \frac{1}{2}QN\); \(BC = \frac{1}{2}QN,AB = \frac{1}{2}MP,DC = \frac{1}{2}MP\). Tứ giác ABCD là hình gì?
Câu 18 :
Cho hình thoi ABCD có chu vi bằng 24cm, đường cao bằng 3cm. Tính \(\widehat {DCA}\).
Câu 19 :
Cho hình thoi ABCD có \(\widehat A\) tù. Biết đường cao kẻ từ đỉnh A đến cạnh CD chia cạnh đó thành hai đoạn bằng nhau. Tính các góc của hình thoi.
Câu 20 :
Cho hình bình hành ABCD có I là giao điểm hai đường chéo. Biết rằng AC = 6cm và BD = 8cm và AD = 5cm. Tìm khẳng định sai ?
Câu 21 :
Cho hình thoi ABCD. Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE = DF. Gọi G, H thứ tự là giao điểm của AE, AF với đường chéo DB. Tứ giác AGCH là hình gì?
Câu 22 :
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của AD, BC. Các đường BE, DF cắt AC tại P, Q . Tứ giác EPFQ là hình thoi nếu \(\widehat {ACD}\) bằng
Lời giải và đáp án
Câu 1 :
Hãy chọn câu sai.
Đáp án : B Phương pháp giải :
Dựa vào dấu hiệu nhận biết hình thoi
Lời giải chi tiết :
Câu A, C, D đúng theo dấu hiệu nhận biết hình thoi. Câu B sai vì 2 đường chéo không cắt nhau tại trung điểm mỗi đường.
Câu 2 :
Điền từ thích hợp vào chỗ trống: “Tứ giác có hai đường chéo … là hình thoi”.
Đáp án : B Phương pháp giải :
: Dựa vào dấu hiệu nhận biết của hình thoi
Lời giải chi tiết :
Vì tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
Câu 3 :
Hình thoi không có tính chất nào dưới đây?
Đáp án : D Phương pháp giải :
Dựa vào tính chất của hình thoi
Lời giải chi tiết :
Hình thoi có tất cả các tính chất của hình bình hành + Các cạnh đối song song và bằng nhau, các góc đối bằng nhau. + Hai đường chéo cắt nhau tại trung điểm mỗi đường. Ngoài ra còn có + Hai đường chéo vuông góc với nhau. + Hai đường chéo là các đường phân giác của các góc của hình thoi.
Câu 4 :
Trong các hình sau, hình nào vừa có tâm đối xứng, vừa có trục đối xứng?
Đáp án : D Phương pháp giải :
Dựa vào tính chất của hình thoi
Lời giải chi tiết :
Hình thoi có tâm đối xứng là giao điểm hai đường chéo, hai trục đối xứng là hai đường chéo của hình thoi.
Đáp án : C Phương pháp giải :
Quan sát các hình để nhận biết hình thoi
Lời giải chi tiết :
Hình 1 là hình thoi vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và vuông góc với nhau. Hình 2 không là hình thoi vì bốn cạnh không bằng nhau. Hình 3 không là hình thoi vì bốn cạnh không bằng nhau.
Câu 6 :
Chọn câu trả lời sai.
Đáp án : D Phương pháp giải :
Dựa vào dấu hiệu nhận biết hình thoi
Lời giải chi tiết :
Vì theo dấu hiệu nhận biết hình thoi Hình bình hành có hai cạnh kề bằng nhau là hình thoi. Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi. Hình chữ nhật là tứ giác có bốn góc bằng nhau nhưng bốn cạnh không bằng nhau nên không là hình thoi.
Câu 7 :
Hình thoi có chu vi là 32 cm, cạnh hình thoi có độ dài là
Đáp án : B Phương pháp giải :
Dựa vào tính chất của hình thoi
Lời giải chi tiết :
Chu vi hình thoi bằng cạnh nhân 4. Vậy cạnh hình thoi là 32 : 4 = 8 cm.
Đáp án : A Phương pháp giải :
Dựa vào dấu hiệu nhận biết của hình thoi.
Lời giải chi tiết :
Tứ giác có bốn cạnh bằng nhau là hình thoi (đúng theo định nghĩa hình thoi)
Câu 9 :
Hình thoi có độ dài hai đường chéo là 24cm và 10cm thì cạnh của hình thoi đó bằng
Đáp án : B Phương pháp giải :
Sử dụng tính chất của hình thoi và áp dụng định lý Pytago trong tam giác vuông.
Lời giải chi tiết :
Giả sử ABCD là hình thoi có hai đường chéo cắt nhau tại H và AC = 10cm, BD = 24cm. Do ABCD là hình thoi nên \(AC \bot BD\) \(\begin{array}{l}AH = \frac{1}{2}AC = \frac{1}{2}.10 = 5cm\\HB = \frac{1}{2}BD = \frac{1}{2}.24 = 12cm\end{array}\) Xét tam giác AH vuông tại H ta có: \(A{B^2} = A{H^2} + H{B^2} = {5^2} + {12^2} = 25 + 144 = 169.\) Suy ra AB= 13 cm.
Câu 10 :
Cho hình thoi ABCD có chu vi bằng 16 cm, đường cao bằng 2 cm. Tính các góc của hình thoi (\(\widehat A > \widehat B\)). Hãy chọn câu trả lời đúng.
Đáp án : A Phương pháp giải :
Dựa vào tính chất của hình thoi.
Lời giải chi tiết :
Vì hình thoi ABCD có chu vi bằng 16 cm nên cạnh hình thoi có độ dài là 16 : 4 = 4 cm. Suy ra AD = 4 cm. Xét tam giác AHD vuông tại H có AH = 2cm, AD = 4cm nên \(AH = \frac{1}{2}AD \Rightarrow \widehat {ADH} = {30^0}\) (theo tính chất). Suy ra \(\widehat {DAB} = {180^0} - \widehat {ADC} = {180^0} - {30^0} = {150^0}.\) (Vì ABCD là hình thoi ) Nên hình thoi ABCD có: \(\widehat A = \widehat C = {150^0};\widehat B = \widehat D = {30^0}\) (Vì hai góc đối bằng nhau).
Câu 11 :
Tứ giác ABCD có AB = CD. Gọi M, N theo thứ tự là trung điểm của BC, DA. Gọi I, K theo thứ tự là trung điểm của AC và BD và\(MK = \frac{1}{2}CD;IM = \frac{1}{2}AB;NI = \frac{1}{2}CD;KN = \frac{1}{2}AB\). Tứ giác KMIN là hình gì?
Đáp án : D Phương pháp giải :
Dựa vào đường trung bình của tam giác chứng minh tứ giác KMIN có
MK = KN = NI = IM suy ra tứ giác KMIN là hình thoi. Lời giải chi tiết :
Xét các tam giác BCD, CAB, ADC, DBA ta có: \(MK = \frac{1}{2}CD;IM = \frac{1}{2}AB;NI = \frac{1}{2}CD;KN = \frac{1}{2}AB\) Mà AB = CD (giả thiết) . Suy ra MK = KN = NI = IM. Tứ giác KMIN có bốn cạnh bằng nhau nên là hình thoi.
Câu 12 :
Các phương án sau, phương án nào sai?
Đáp án : D Phương pháp giải :
Dựa vào tính chất của hình thoi
Lời giải chi tiết :
Định lí: + Hình thoi có hai trục đối xứng là hai đường chéo của hình thoi. + Có một tâm đối xứng là giao điểm của hai đường chéo. Mở rộng: + Trong hình chữ nhật, các trung điểm của các cạnh hình chữ nhật là các đỉnh của một hình thoi. + Trong hình thoi, các trung điểm của bốn cạnh hình thoi là các hình chữ nhật. → Đáp án D sai.
Câu 13 :
Hai đường chéo của hình thoi có độ dài lần lượt là 8cm và 10cm. Diện tích của hình thoi đó là ?
Đáp án : B Phương pháp giải :
Áp dụng công thức tính diện tích của hình thoi: \({S_{hthoi}}\) bằng \(\frac{1}{2}\) tích hai đường chéo của hình thoi.
Lời giải chi tiết :
Diện tích của hình thoi là:
\(\left( {8.10} \right):2 = 40c{m^2}\)
Câu 14 :
Một hình thoi có diện tích là \(\frac{5}{3}d{m^2}\). Biết độ dài một đường chéo bằng \(\frac{{25}}{2}dm\). Tính độ dài đường chéo còn lại.
Đáp án : A Phương pháp giải :
Từ công thức tính diện tích của hình thoi suy ra công thức tính độ dài một đường chéo khi biết độ dài một đường chéo.
Lời giải chi tiết :
Độ dài đường chéo còn lại là: \(\frac{5}{3}.2:\frac{{25}}{2} = \frac{4}{{15}}(dm)\)
Câu 15 :
Cho hình thoi ABCD có O là giao điểm hai đường chéo, biết AC = 16cm và OB = 6cm. Tính CD?
Đáp án : D Phương pháp giải :
Áp dụng tính chất của hình thoi và định lí Pytago trong tam giác vuông để tìm độ dài một cạnh của hình thoi.
Lời giải chi tiết :
Do ABCD là hình thoi nên: \(AO = OC = \frac{1}{2}AC = \frac{1}{{2}}.16 = 8cm\) Áp dụng định lí Pytago vào tam giác vuông ABO ta có: \(A{B^2} = O{A^2} + O{B^2} = {8^2} + {6^2} = 64 + 36 = 100 \Rightarrow AB = 10cm\) Vì ABCD là hình thoi nên AB = CD = 10cm
Câu 16 :
Cho tam giác ABC vuông ở A, trung tuyến AM. Gọi D là trung điểm của AB và MD // AC, \({M'}\) là điểm đối xứng với M qua D. Tứ giác \(AMBM'\) là hình gì?
Đáp án : A Phương pháp giải :
Chứng minh tứ giác \(AMBM'\) là hình bình hành có \(M{M'} \bot AB\)nên \(AMBM'\) là hình thoi Lời giải chi tiết :
Vì \({M'}\)đối xứng M qua D nên \(DM = D{M'}\)(1) Ta có: MD // AC Mặt khác \(\Delta ABC\) vuông ở A nên \(AB \bot AC\).(2) Từ (1) và (2) suy ra \(DM \bot AB \Rightarrow M{M'} \bot AB.\) Vì D là trung điểm của AB (gt) và D là trung điểm của M\({M'}\) nên tứ giác \(AMB{M'}\) là hình bình hành. Mặt khác \(M{M'} \bot AB\) nên \(AMB{M'}\) là hình thoi. (Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.)
Câu 17 :
Cho hình thang cân MNPQ. Gọi A, B, C, D lần lượt là các điểm thuộc các cạnh MN, NP, PQ, QM và \(AD = \frac{1}{2}QN\); \(BC = \frac{1}{2}QN,AB = \frac{1}{2}MP,DC = \frac{1}{2}MP\). Tứ giác ABCD là hình gì?
Đáp án : D Phương pháp giải :
Chứng minh tứ giác ABCD có bốn cạnh bằng nhau nên ABCD là hình thoi.
Lời giải chi tiết :
Do MNPQ là hình thang cân nên MP = NQ. (hình thang cân có hai đường chéo bằng nhau). (1) Xét các tam giác MNQ ; PQN, MNP, QMP ta có: \(AD = \frac{1}{2}QN\); \(BC = \frac{1}{2}QN,AB = \frac{1}{2}MP,DC = \frac{1}{2}MP\) Suy ra AB = BC = CD = DA. Do đó ABCD là hình thoi. (Tứ giác có bốn cạnh bằng nhau là hình thoi.)
Câu 18 :
Cho hình thoi ABCD có chu vi bằng 24cm, đường cao bằng 3cm. Tính \(\widehat {DCA}\).
Đáp án : D Phương pháp giải :
Tính góc A, góc C của hình thoi và sử dụng AC là tia phân giác của \(\widehat {DCB}\)
Lời giải chi tiết :
Vì hình thoi ABCD có chu vi bằng 24cm nên cạnh hình thoi có độ dài là 24 : 4 = 6cm. Suy ra AD = 6cm. Xét tam giác AHD vuông tại H có. \(AH = \frac{1}{2}AD \Rightarrow \widehat {ADH} = {30^0}\) ( theo tính chất). Suy ra \(\widehat {DAB} = {180^0} - \widehat {ADC} = {180^0} - {30^0} = {150^0}\).(Vì ABCD là hình thoi ) Nên hình thoi ABCD có: \(\widehat A = \widehat C = {150^o}\); \(\widehat B = \widehat D = {30^o}\) (Vì hai góc đối bằng nhau). Lại có tia CA là tia phân giác \(\widehat {DCB}\) (tính chất hình thoi). Nên \(\widehat {DCA} = \frac{1}{2}\widehat {DCB} = \frac{1}{2}{.150^0} = {75^0}\) Hai đường chéo là các đường phân giác của các góc của hình thoi
Câu 19 :
Cho hình thoi ABCD có \(\widehat A\) tù. Biết đường cao kẻ từ đỉnh A đến cạnh CD chia cạnh đó thành hai đoạn bằng nhau. Tính các góc của hình thoi.
Đáp án : D Phương pháp giải :
Áp dụng tính chất của hình thoi để tính các góc.
Lời giải chi tiết :
Gọi H là chân đường cao kẻ từ A đến cạnh CD. Từ giả thiết ta có: \(AH \bot CD\), CH = HD suy ra AH là đường trung trực của đoạn CD nên AC = AD (1) Do ABCD là hình thoi nên AD = CD (2) Từ (1) và (2) suy ra AD = CD = AC nên \(\Delta ACD\)là tam giác đều, do đó\(\widehat D = {60^0}\). Vì AB // CD nên \(\widehat {DAB} + \widehat D = {180^0}\) (hai góc trong cùng phía) \( \Rightarrow \widehat {DAB} = {180^0} - \widehat D = {180^0} - {60^0} = {120^0}\). Áp dụng tính chất về góc vào hình thoi ABCD ta được: \(\widehat B = \widehat D = {60^0},\widehat A = \widehat C = {120^0}\)
Câu 20 :
Cho hình bình hành ABCD có I là giao điểm hai đường chéo. Biết rằng AC = 6cm và BD = 8cm và AD = 5cm. Tìm khẳng định sai ?
Đáp án : D Lời giải chi tiết :
Theo tính chất hình bình hành ta có: I là trung điểm của AC và BD. Suy ra: \(\begin{array}{l}AI = \frac{1}{2}AC = \frac{1}{2}.6 = 3cm\\DI = \frac{1}{2}B{\rm{D}} = \frac{1}{2}.8 = 4cm\end{array}\) Xét tam giác AID có: \(A{I^2} + I{{\rm{D}}^2} = A{{\rm{D}}^2}\left( {{3^2} + {4^2} = {5^2}} \right)\) Suy ra: tam giác AID là tam giác vuông: AI ⊥ DI hay AC ⊥ BD Hình bình hành ABCD có 2 đường chéo AC và BD vuông góc với nhau nên là hình thoi. Suy ra: AB = BC = CD = DA = 5cm Hai đường chéo của hình thoi cắt nhau tại trung điểm của mỗi đường.
Câu 21 :
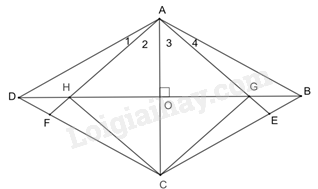
Cho hình thoi ABCD. Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE = DF. Gọi G, H thứ tự là giao điểm của AE, AF với đường chéo DB. Tứ giác AGCH là hình gì?
Đáp án : A Phương pháp giải :
Áp dụng các dấu hiệu của hình thoi
Lời giải chi tiết :
Gọi O là giao điểm của AC và BD thì \(AC \bot BD\) (do O là giao điểm của hai đường chéo của hình thoi) Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD, ta được: \(AB = AD;\widehat B = \widehat D;BE = DF\) Từ đó suy ra \(\Delta ABE = \Delta ADF\)(c-g-c). Suy ra \(\widehat {A{}_1} = \widehat {{A_4}}\)( hai góc tương ứng). Mà AC là phân giác của \(\widehat {BAD} \Rightarrow \widehat {{A_2}} = \widehat {{A_3}}\)(1) Xét tam giác AGH có AO là đường cao, đồng thời là đường phân giác nên tam giác AGH cân tại A. Suy ra HO = OG (2) Do ABCD là hình thoi nên AO = OC (tính chất đường chéo của hình thoi) (3) Từ (1), (2), (3) suy ra: AHCG là hình thoi.
Câu 22 :
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của AD, BC. Các đường BE, DF cắt AC tại P, Q . Tứ giác EPFQ là hình thoi nếu \(\widehat {ACD}\) bằng
Đáp án : B Phương pháp giải :
Chứng minh EPFQ là hình thoi từ đó suy ra số đo \(\widehat {ACD}\)
Lời giải chi tiết :
Gọi O là giao điểm của hai đường chéo AC và BD. Vì ABCD là hình bình hành nên O là trung điểm của AC, BD và AD //CB, AD = BC Xét tứ giác EDFB có ED // FB, \(ED = FB\left( { = \frac{1}{2}AD = \frac{1}{2}BC} \right)\). Nên EDFB là hình bình hành. Suy ra: BE = DF, BE // DF. Xét \(\Delta ABD\)có P là giao điểm hai đường trung tuyến BE, AO nên P là trọng tâm \(\Delta ABD \Rightarrow EP = \frac{1}{3}BE\). Xét \(\Delta CBD\)có Q là giao điểm hai đường trung tuyến DF, CO nên Q là trọng tâm \(\Delta CBD \Rightarrow QF = \frac{1}{3}DF\). Mà BE = DF (cmt) \( \Rightarrow \)EP = QF. Xét tứ giác EPFQ có \( \Rightarrow \)EP = QF, EP // QF \( \Rightarrow \)EPFQ là hình bình hành. Để hình bình hành EPFQ là hình thoi thì \({\rm{EF}} \bot PQ\). Mà EF // CD (do hình bình hành ABCD có AB //CD, E là trung điểm AD, F là trung điểm BC ). Nên \(CD \bot PQ\) hay \(CD \bot AC \Rightarrow \widehat {ACD} = {90^0}\).
|
