Trắc nghiệm Bài 4: Đồ thị của hàm số bậc nhất y=ax+b(a khác 0) Toán 8 Cánh diềuĐề bài
Câu 2 :
Cho đồ thị hàm số y=x+1. Điểm nào dưới đây thuộc đồ thị hàm số trên?
Câu 3 :
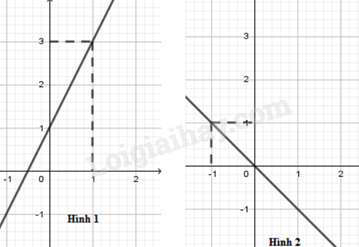
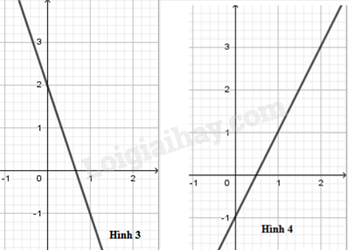
Một người đi bộ trên đường thẳng với vận tốc v (km/h). Gọi s (km) là quãng đường đi được trong t (giờ). Khi đó, đồ thị của hàm số s theo biến t với v=5 đường thẳng nào trong hình vẽ dưới đây?
Câu 4 :
Cho đường thẳng d: y=2x+m. Đường thẳng d đi qua điểm A(1; 5). Chọn đáp án đúng.
Câu 5 :
Cho hàm số bậc nhất y=(2−m)x+m. Xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ 4.
Câu 6 :
Đồ thị của hàm số y=ax+b(a≠0) là:
Câu 7 :
Đồ thị hàm số y=ax+b(a≠0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng:
Câu 8 :
Cho hai đường thẳng d1:y=x−1 và d2:y=3−4x. Tung độ giao điểm của hai đường thẳng d1 và d2 là:
Câu 9 :
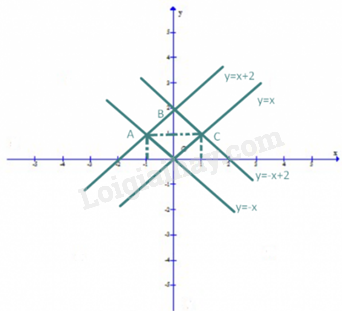
Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ: y=x;y=x+2;y=−x+2;y=−x. Bốn đồ thị nói trên cắt nhau tại các điểm O(0; 0), A, B, C. Tứ giác có 4 đỉnh O, A, B, C là hình gì?
Câu 10 :
Cho hàm số y=mx+2 có đồ thị là đường thẳng d1 và hàm số y=12x+1 có đồ thị là đường thẳng d2. Để đường thẳng d1 và đường thẳng d2 cắt nhau tại một điểm có hoành độ bằng 4 là:
Câu 11 :
Cho hàm số y=(m−1)x−1 có đồ thị là đường thẳng d1 và hàm số y=x+1 có đồ thị là đường thẳng d2. Để đường thẳng d1 và đường thẳng d2 cắt nhau tại một điểm có tung độ bằng 4 là:
Câu 12 :
Cho đường thẳng d1:y=−x+3 và d2:y=4−3x. Gọi A và B lần lượt là giao điểm của d1 và d2 với trục hoành. Tổng hoành độ giao điểm của hai điểm A và B là:
Câu 13 :
Cho đường thẳng d: y=−2x−4. Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Diện tích tam giác OAB là:
Câu 14 :
Với giá trị nào của m thì ba đường thẳng d1:y=(m−1)x−3;d2:y=2x+1;d3:y=x−3 giao nhau tại một điểm?
Câu 15 :
Gọi d1 là đồ thị của hàm số y=mx−1 và d2 là đồ thị hàm số y=12x+2. Để M(2; 3) là giao điểm của d1 và d2 thì giá trị của m là:
Câu 16 :
Cho đường thẳng d được xác định bởi y=2x+10. Đường thẳng d’ đối xứng với đường thẳng d qua trục hoành là:
Câu 17 :
Cho đường thẳng d xác định bởi y=2x+4. Đường thẳng d’ đối xứng với đường thẳng d qua đường thẳng y=x là:
Câu 18 :
Cho đường thẳng y=mx+m+1(1) (m là tham số). Đường thẳng (1) luôn đi qua một điểm cố định mới mọi giá trị của m. Điểm cố định đó là:
Câu 19 :
Tìm x sao cho ba điểm A(x; 14), B(-5; 20), C(7; -16) thẳng hàng.
Câu 20 :
Có bao nhiêu đường thẳng đi qua A(4; 3), cắt trục tung tại điểm có tung độ là một số nguyên dương, cắt trục hoành tại điểm có hoành độ làm một số nguyên tố.
Câu 21 :
Hệ số góc của đường thẳng y=2x+1 là:
Câu 22 :
Tìm hàm số bậc nhất có hệ số góc bằng 2 và có đồ thị cắt trục tung tại điểm có tung độ bằng −1.
Câu 23 :
Cho đường thẳng y=ax+b(a≠0) có hệ số góc là:
Câu 24 :
Đường thẳng y=ax+b có hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là:
Câu 25 :
Chọn khẳng định đúng nhất:
Câu 27 :
Giá trị của m để đường thẳng y=(m+1)x+2(m≠−1) song song với đường thẳng y=−2x+1 là:
Câu 28 :
Tìm các giá trị của m để đường thẳng y=(m−1)x−2(m≠1) cắt đường thẳng y=2x là:
Câu 29 :
Hai đường thẳng, y=2mx+1(m≠0) và y=(m+1)x+1(m≠−1) trùng nhau khi:
Câu 31 :
Cho hai hàm số bậc nhất y=2mx+1 và y=(m+1)x+m, có bao nhiêu giá trị của m để đồ thị của hai hàm số đã cho là hai đường thẳng song song?
Câu 32 :
Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng y=3x+1 và đi qua điểm (1;7)?
Câu 33 :
Hệ số góc của đường thẳng d biết d đi qua gốc tọa độ O và điểm M(2; 6) là:
Câu 34 :
Đường thẳng y=2(m+1)x+m−2(m≠−1) đi qua điểm A(1; 9) có hệ số góc là:
Câu 35 :
Cho hai đồ thị hàm số bậc nhất là hai đường thẳng d: y=(m−2)x−m và d′:y=−2x−2mx+3. Với giá trị nào của m thì d cắt d’
Câu 36 :
Cho hai đường thẳng d: y=(m+2)x+m và d’: y=−2x−2m+1. Với giá trị nào của m thì d trùng với d’?
Câu 37 :
Cho hàm số bậc nhất y=2ax+a−1 có đồ thị hàm số là đường d. Đường thẳng d có hệ số góc gấp hai lần hệ số góc của đường thẳng d’: y−4x+3=0 Khi đó, điểm A(x; 6) thuộc đường thẳng d thì giá trị của x là:
Câu 38 :
Hệ số góc của đường thẳng x3+y2=1 là:
Câu 39 :
Các điểm A(m; 3) và B(1; m) nằm trên đường thẳng có hệ số góc m>0. Tìm m.
Câu 40 :
Cho hàm số bậc nhất y=mx+3 có đồ thị là đường thẳng d. Biết rằng đường thẳng d song song với đường thẳng y=−x. Gọi A là giao điểm của đường thẳng d với đồ thị của hàm số y=x+1. B là giao điểm của đường thẳng d với trục Ox. Diện tích tam giác OAB là:
Câu 41 :
Cho hàm số bậc nhất y=12m2x+m10−m4−14mx+3(1) Tìm giá trị của m để đồ thị hàm số (1) có hệ số góc đạt giá trị nhỏ nhất.
Lời giải và đáp án
Đáp án : B Phương pháp giải :
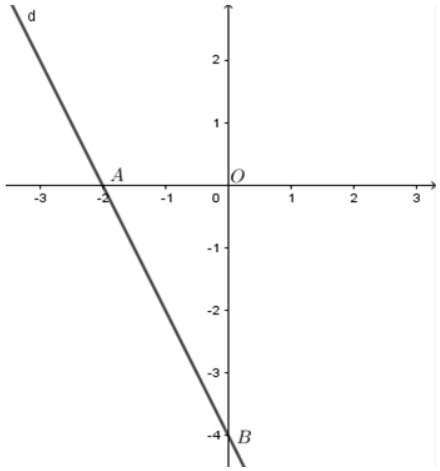
Sử dụng cách vẽ đồ thị hàm số bậc nhất y=ax+b(a≠0): Để vẽ đồ thị hàm số y=ax+b(a≠0), ta có thể xác định hai điểm P(0;b) và Q(−ba;0)
Lời giải chi tiết :
Đồ thị của hàm số y=1+2x đi qua các điểm có tọa độ (0; 1) và (−12;0) nên hình 1 là đồ thị của hàm số y=1+2x
Câu 2 :
Cho đồ thị hàm số y=x+1. Điểm nào dưới đây thuộc đồ thị hàm số trên?
Đáp án : D Phương pháp giải :
Sử dụng cách vẽ đồ thị hàm số bậc nhất y=ax+b(a≠0): Để vẽ đồ thị hàm số y=ax+b(a≠0), ta có thể xác định hai điểm P(0;b) và Q(−ba;0)
Lời giải chi tiết :
Với x = 0, ta có y = 0 + 1 = 1 nên O(0; 0) không thuộc đồ thị hàm số y = x + 1. Với x = -1, ta có y = -1 + 1 = 0 nên điểm C(-1; 0) thuộc đồ thị hàm số y=x+1.
Câu 3 :
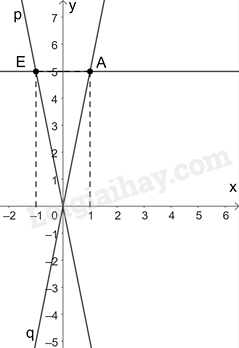
Một người đi bộ trên đường thẳng với vận tốc v (km/h). Gọi s (km) là quãng đường đi được trong t (giờ). Khi đó, đồ thị của hàm số s theo biến t với v=5 đường thẳng nào trong hình vẽ dưới đây?
Đáp án : D Phương pháp giải :
Sử dụng cách vẽ đồ thị hàm số bậc nhất y=ax+b(a≠0): Để vẽ đồ thị hàm số y=ax+b(a≠0), ta có thể xác định hai điểm P(0;b) và Q(−ba;0)
Lời giải chi tiết :
Hàm số s theo biến t với v=5 là: s=5t Đồ thị hàm số s=5t đi qua 2 điểm O(0; 0) và A(1; 5) Do đó, đồ thị hàm số s=5t là đường thẳng q.
Câu 4 :
Cho đường thẳng d: y=2x+m. Đường thẳng d đi qua điểm A(1; 5). Chọn đáp án đúng.
Đáp án : C Phương pháp giải :
Đồ thị hàm số y=ax+b(a≠0) đi qua điểm M(x0;y0) khi và chỉ khi y0=ax0+b
Lời giải chi tiết :
Đường thẳng d đi qua điểm A(1; 5) nên 5=2.1+m m=3
Câu 5 :
Cho hàm số bậc nhất y=(2−m)x+m. Xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ 4.
Đáp án : A Phương pháp giải :
Đồ thị hàm số y=ax+b(a≠0) đi qua điểm M(x0;y0) khi và chỉ khi y0=ax0+b
Lời giải chi tiết :
Hàm số y=(2−m)x+m là hàm số bậc nhất khi m≠2 Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 4 nên x=4;y=0 Do đó, 0=4(2−m)+m 8−4m+m=0 3m=8 m=83 (thỏa mãn)
Câu 6 :
Đồ thị của hàm số y=ax+b(a≠0) là:
Đáp án : A Phương pháp giải :
Sử dụng nhận xét về đồ thị hàm số bậc nhất: Đồ thị của hàm số y=ax+b(a≠0) là một đường thẳng.
Lời giải chi tiết :
Đồ thị của hàm số y=ax+b(a≠0) là một đường thẳng.
Câu 7 :
Đồ thị hàm số y=ax+b(a≠0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng:
Đáp án : C Phương pháp giải :
Sử dụng tính chất của đồ thị hàm số bậc nhất: Đồ thị hàm số y=ax+b(a≠0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng b.
Lời giải chi tiết :
Đồ thị hàm số y=ax+b(a≠0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng b.
Câu 8 :
Cho hai đường thẳng d1:y=x−1 và d2:y=3−4x. Tung độ giao điểm của hai đường thẳng d1 và d2 là:
Đáp án : D Phương pháp giải :
Tìm tọa độ giao điểm của hai đường thẳng theo các bước:
Bước 1: Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm Bước 2: Thay hoành độ giao điểm vừa tìm được vào một trong hai hàm số ta tìm được tung độ giao điểm. Lời giải chi tiết :
Xét phương trình hoành độ giao điểm của d1 và d2: x−1=3−4x 5x=4 x=45 Với x=45 thì y=45−1=−15 Vậy tung độ giao điểm của hai đường thẳng d1 và d2 là −15
Câu 9 :
Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ: y=x;y=x+2;y=−x+2;y=−x. Bốn đồ thị nói trên cắt nhau tại các điểm O(0; 0), A, B, C. Tứ giác có 4 đỉnh O, A, B, C là hình gì?
Đáp án : A Phương pháp giải :
Sử dụng cách vẽ đồ thị hàm số bậc nhất y=ax+b(a≠0): Để vẽ đồ thị hàm số y=ax+b(a≠0), ta có thể xác định hai điểm P(0;b) và Q(−ba;0)
Lời giải chi tiết :
Với hàm số y = x, cho x = 1 thì y = 1. Đồ thị hàm số y = x đi qua các điểm O(0;0) và C(1;1) Với hàm số y = x+2, cho x = 0 thì y = 2, cho x = -1 thì y = 1. Đồ thị hàm số y = x +2 đi qua các điểm B(0;2) và A(-1;1) Với hàm số y = -x, cho x = -1 thì y = 1. Đồ thị hàm số y = -x đi qua các điểm O(0;0) và A(-1;1) Với hàm số y = -x +2, cho x =0 thì y = 2, cho x = 1 thì y = 1. Đồ thị hàm số y = -x +2 đi qua các điểm B (0;2) và C(1;1) Đồ thị hàm số:
Từ đồ thị trên ta thấy: Đường thẳng y=x song song với đường thẳng y=x+2 nên OC//AB Đường thẳng y=−x song song với đường thẳng y=−x+2 nên OA//BC Tứ giá OABC có: OC//AB, OA//BC và OB⊥AC nên tứ giác OABC là hình thoi
Câu 10 :
Cho hàm số y=mx+2 có đồ thị là đường thẳng d1 và hàm số y=12x+1 có đồ thị là đường thẳng d2. Để đường thẳng d1 và đường thẳng d2 cắt nhau tại một điểm có hoành độ bằng 4 là:
Đáp án : B Phương pháp giải :
+ Bước 1: Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm + Bước 2: Thay hoành độ giao điểm vào phương trình hoành độ giao điểm để tìm m. Lời giải chi tiết :
Phương trình hoành độ giao điểm của d1 và d2 là: mx+2=12x+1 (1) Để đường thẳng d1 và đường thẳng d2 cắt nhau tại một điểm có hoành độ bằng 4 thì x=4 thỏa mãn phương trình (*). Do đó, 4m+2=12.4+1 4m=1 m=14
Câu 11 :
Cho hàm số y=(m−1)x−1 có đồ thị là đường thẳng d1 và hàm số y=x+1 có đồ thị là đường thẳng d2. Để đường thẳng d1 và đường thẳng d2 cắt nhau tại một điểm có tung độ bằng 4 là:
Đáp án : B Phương pháp giải :
Đồ thị hàm số y=ax+b(a≠0) đi qua điểm M(x0;y0) khi và chỉ khi y0=ax0+b
Lời giải chi tiết :
Để đường thẳng d1 và đường thẳng d2 cắt nhau tại một điểm có tung độ bằng 4 nên thay y=4 vào y=x+1 ta có: 4=x+1, x=3 Do đó, tọa độ giao điểm của d1 và d2 là (3;4) Thay x=3,y=4 vào y=(m−1)x−1 ta có: 4=3(m−1)−1 3m−3−1=4 m=83
Câu 12 :
Cho đường thẳng d1:y=−x+3 và d2:y=4−3x. Gọi A và B lần lượt là giao điểm của d1 và d2 với trục hoành. Tổng hoành độ giao điểm của hai điểm A và B là:
Đáp án : C Phương pháp giải :
Sử dụng cách vẽ đồ thị hàm số bậc nhất y=ax+b(a≠0): Để vẽ đồ thị hàm số y=ax+b(a≠0), ta có thể xác định hai điểm P(0;b) và Q(−ba;0)
Lời giải chi tiết :
Đường thẳng d1 cắt trục hoành tại điểm A nên A có tung độ y=0. Do đó, 0=−x+3;x=3 nên hoành độ của điểm A là x=3 Đường thẳng d2 cắt trục hoành tại điểm B nên B có tung độ y=0. Do đó, 0=4−3x;x=43 nên hoành độ của điểm B là x=43 Do đó, tổng hoành độ giao điểm của A và B là 133
Câu 13 :
Cho đường thẳng d: y=−2x−4. Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Diện tích tam giác OAB là:
Đáp án : A Phương pháp giải :
+ Bước 1: Tìm tọa độ giao điểm A, B + Bước 2: Sử dụng công thức tính diện tích tam giác AOB vuông tại O: S=OA.OB2 Lời giải chi tiết :
A là giao điểm của d với trục hoành nên 0=−2x−4,x=−2 nên A(−2;0) B là giao điểm của d với trục tung nên y=−2.0−4=−4 nên B(0;−4) Do đó, OA=2,OB=4 Vì tam giác AOB vuông tại O nên diện tích tam giác OAB là: S=OA.OB2=2.42=4 (đvdt)
Câu 14 :
Với giá trị nào của m thì ba đường thẳng d1:y=(m−1)x−3;d2:y=2x+1;d3:y=x−3 giao nhau tại một điểm?
Đáp án : C Phương pháp giải :
+ Bước 1: Tìm tọa độ giao điểm của hai đường thẳng trong ba đường thẳng đã cho. + Bước 2: Thay tọa độ giao điểm vừa tìm được vào đường thẳng còn lại để tìm m. Lời giải chi tiết :
Xét phương trình hoành độ giao điểm của d2 và d3: 2x+1=x−3 x=−4 Với x=−4 vào y=x−3 ta có: y=−4−3=−7 Do đó, giao điểm của d2 và d3 là M(-4; -7) Để ba đường thẳng d1:y=(m−1)x−3;d2:y=2x+1;d3:y=x−3 giao nhau tại một điểm thì M thuộc d1. Do đó, −7=−4(m−1)−3 −4m+4−3=−7 −4m=−8 m=2
Câu 15 :
Gọi d1 là đồ thị của hàm số y=mx−1 và d2 là đồ thị hàm số y=12x+2. Để M(2; 3) là giao điểm của d1 và d2 thì giá trị của m là:
Đáp án : C Phương pháp giải :
Để M(x0;y0) là giao điểm của hai đường thẳng d1 và d2 ta thay tọa độ của M vào từng hàm số tương ứng để tìm m.
Lời giải chi tiết :
+ Nhận thấy M thuộc d2 Thay tọa độ M vào y=mx−1 ta có: 3=m.2−1 2m=4 m=2
Câu 16 :
Cho đường thẳng d được xác định bởi y=2x+10. Đường thẳng d’ đối xứng với đường thẳng d qua trục hoành là:
Đáp án : B Phương pháp giải :
+ Điểm đối xứng với điểm (x; y) qua trục hoành là điểm (x; -y)
+ Thay y bởi −y vào hàm số đã cho ta tìm được đường thẳng cần tìm. Lời giải chi tiết :
Điểm đối xứng với điểm (x; y) qua trục hoành là điểm (x; -y) Xét hàm số y=2x+10, thay y bởi −y ta được: −y=2x+10 hay y=−2x−10
Câu 17 :
Cho đường thẳng d xác định bởi y=2x+4. Đường thẳng d’ đối xứng với đường thẳng d qua đường thẳng y=x là:
Đáp án : C Phương pháp giải :
+ Điểm đối xứng với điểm (x; y) qua đường thẳng y=x là (y;x)
+ Thay x bởi y, thay y bởi x trong hàm số của đường thẳng đã cho, ta tìm được hàm số của đường thẳng cần tìm. Lời giải chi tiết :
Điểm đối xứng với điểm (x; y) qua đường thẳng y=x là (y;x) Xét hàm số, y=2x+4, thay x bởi y, thay y bởi x ta có: x=2y+4 hay y=12x−2
Câu 18 :
Cho đường thẳng y=mx+m+1(1) (m là tham số). Đường thẳng (1) luôn đi qua một điểm cố định mới mọi giá trị của m. Điểm cố định đó là:
Đáp án : D Phương pháp giải :
Gọi điểm (x0;y0) là điểm cố định mà đồ thị hàm số y=f(x) luôn đi qua.
Do đó, y0=f(x0;m) có nghiệm đúng với mọi m. Lời giải chi tiết :
Gọi điểm N(x0;y0) là điểm cố định của đường thẳng (1). Ta có: y0=mx0+m+1 y0−mx0−m−1=0 −(x0+1)m+y0−1=0 Để phương trình luôn đúng với mọi m thì {x0+1=0y0−1=0 Suy ra {x0=−1y0=1 Vậy đường thẳng (1) luôn đi qua điểm cố định (-1; 1).
Câu 19 :
Tìm x sao cho ba điểm A(x; 14), B(-5; 20), C(7; -16) thẳng hàng.
Đáp án : C Phương pháp giải :
+ Tìm hàm số mà có đồ thị đi qua hai điểm B, C. + Để 3 điểm A, B, C thẳng hàng thì điểm A thuộc đường thẳng BC, do đó thay tọa độ điểm A vào hàm số đã tìm được để tìm x. Lời giải chi tiết :
Đường thẳng BC có dạng: y=ax+b Vì điểm B(-5; 20) thuộc đường thẳng BC nên 20=−5a+b, b=20+5a(1) Vì điểm C(7; -16) thuộc đường thẳng BC nên −16=7a+b(2) Thay (1) vào (2) ta có: −16=7a+20+5a 12a=−36 a=−3 nên b=20+5.(−3)=5 Do đó đường thẳng BC có dạng: y=−3x+5 Để 3 điểm A, B, C thẳng hàng thì điểm A(x; 14) thuộc đường thẳng BC. Do đó, 14=−3x+5 −3x=9 x=−3
Câu 20 :
Có bao nhiêu đường thẳng đi qua A(4; 3), cắt trục tung tại điểm có tung độ là một số nguyên dương, cắt trục hoành tại điểm có hoành độ làm một số nguyên tố.
Đáp án : C Phương pháp giải :
Đường thẳng phải tìm cắt trục hoành tại điểm có hoành độ bằng a, cắt trục tung tại điểm có tung độ bằng b thì đường thẳng có dạng xa+yb=1
Lời giải chi tiết :
Chứng minh dễ dàng được: Đường thẳng phải tìm cắt trục hoành tại điểm có hoành độ bằng a, cắt trục tung tại điểm có tung độ bằng b thì đường thẳng có dạng xa+yb=1 Điểm A(4; 3) thuộc đường thẳng nên 4a+3b=1. Do đó, b=3aa−4=3+12a−4 Do a là số nguyên tố nên a≥2,a−4≥−2 Lần lượt cho a−4 nhận các giá trị ±2;±1;3;4;6;12 với chú ý rằng a là số nguyên tố và b>0, ta tìm được {a=5b=15 và {a=7b=7 Do đó ta tìm được hai đường thẳng x5+y15=1 (hay y=−3x+15) và x7+y7=1 (hay y=−x+7)
Câu 21 :
Hệ số góc của đường thẳng y=2x+1 là:
Đáp án : B Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng y=ax+b(a≠0)
Lời giải chi tiết :
Hệ số góc của đường thẳng y=2x+1 là: 2
Câu 22 :
Tìm hàm số bậc nhất có hệ số góc bằng 2 và có đồ thị cắt trục tung tại điểm có tung độ bằng −1.
Đáp án : D Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng y=ax+b(a≠0)
Lời giải chi tiết :
Hàm số bậc nhất có dạng y=ax+b(a≠0) Vì đường thẳng y=ax+b có hệ số góc bằng 2 nên a=2(tm) Do đó hàm số: y=2x+b Đường thẳng y=2x+b cắt trục tung tại điểm có tung độ bằng −1 nên y=−1;x=0 Ta có: −1=2.0+b b=−1 Do đó, hàm số cần tìm là: y=2x−1
Câu 23 :
Cho đường thẳng y=ax+b(a≠0) có hệ số góc là:
Đáp án : A Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng y=ax+b(a≠0)
Lời giải chi tiết :
Ta gọi a là hệ số góc của đường thẳng y=ax+b(a≠0)
Câu 24 :
Đường thẳng y=ax+b có hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là:
Đáp án : C Phương pháp giải :
Sử dụng nhận xét hệ số góc của đường thẳng: Khi hệ số góc a dương, đường thẳng y=ax+b đi lên từ trái sang phải, góc tạo bởi đường thẳng này và trục Ox là góc nhọn.
Lời giải chi tiết :
Đường thẳng y=ax+b có hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là góc nhọn
Câu 25 :
Chọn khẳng định đúng nhất:
Đáp án : C Phương pháp giải :
+ Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng y=ax+b(a≠0) và y′=a′x+b′(a′≠0) song song với nhau khi a=a′,b≠b′ và ngược lại, trùng nhau khi a=a′,b=b′ và ngược lại + Sử dụng nhận biết về hai đường thẳng cắt nhau: Hai đường thẳng y=ax+b(a≠0) và y′=a′x+b′(a′≠0) cắt nhau khi a≠a′ và ngược lại. Lời giải chi tiết :
Hai đường thẳng y=ax+b(a≠0) và y′=a′x+b′(a′≠0) song song với nhau khi a=a′,b≠b′ và ngược lại, trùng nhau khi a=a′,b=b′ và ngược lại Hai đường thẳng y=ax+b(a≠0) và y′=a′x+b′(a′≠0) cắt nhau khi a≠a′ và ngược lại.
Đáp án : B Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng y=ax+b(a≠0)
Lời giải chi tiết :
Ta có: y=3x+13=x+13 nên hệ số góc của đường thẳng là 1
Câu 27 :
Giá trị của m để đường thẳng y=(m+1)x+2(m≠−1) song song với đường thẳng y=−2x+1 là:
Đáp án : D Phương pháp giải :
+ Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng y=ax+b(a≠0) và y′=a′x+b′(a′≠0) song song với nhau khi a=a′,b≠b′ và ngược lại Lời giải chi tiết :
Để đường thẳng y=(m+1)x+2(m≠−1) song song với đường thẳng y=−2x+1 thì 2≠1 (luôn đúng) và m+1=−2 m=−3 (thỏa mãn)
Câu 28 :
Tìm các giá trị của m để đường thẳng y=(m−1)x−2(m≠1) cắt đường thẳng y=2x là:
Đáp án : C Phương pháp giải :
+ Sử dụng nhận biết về hai đường thẳng cắt nhau: Hai đường thẳng y=ax+b(a≠0) và y′=a′x+b′(a′≠0) cắt nhau khi a≠a′ và ngược lại.
Lời giải chi tiết :
Để đường thẳng y=(m−1)x−2(m≠1) cắt đường thẳng y=2x thì m−1≠2 m≠3 (thỏa mãn)
Câu 29 :
Hai đường thẳng, y=2mx+1(m≠0) và y=(m+1)x+1(m≠−1) trùng nhau khi:
Đáp án : C Phương pháp giải :
+ Sử dụng nhận biết về hai đường thẳng trùng nhau: Hai đường thẳng y=ax+b(a≠0) và y′=a′x+b′(a′≠0) trùng nhau khi a=a′,b=b′ và ngược lại
Lời giải chi tiết :
Hai đường thẳng, y=2mx+1(m≠0) và y=(m+1)x+1 trùng nhau khi: 1=1 (luôn đúng) và 2m=m+1 m=1 (thỏa mãn)
Đáp án : D Phương pháp giải :
Sử dụng nhận biết về hai đường thẳng cắt nhau: Hai đường thẳng y=ax+b(a≠0) và y′=a′x+b′(a′≠0) cắt nhau khi a≠a′ và ngược lại.
Lời giải chi tiết :
Các cặp 2 đường thẳng cắt nhau là: y=x+5 và y=−x+5; y=x+5 và y=−x+3; y=−x+5 và y=x+7; y=x+7 và y=−x+3 Do đó, có 4 cặp hai đường thẳng cắt nhau.
Câu 31 :
Cho hai hàm số bậc nhất y=2mx+1 và y=(m+1)x+m, có bao nhiêu giá trị của m để đồ thị của hai hàm số đã cho là hai đường thẳng song song?
Đáp án : A Phương pháp giải :
Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng y=ax+b(a≠0) và y′=a′x+b′(a′≠0) song song với nhau khi a=a′,b≠b′ và ngược lại Lời giải chi tiết :
Hàm số y=2mx+1 là hàm số bậc nhất khi m≠0, hàm số y=(m+1)x+m là hàm số bậc nhất khi m≠−1 Để hai đường thẳng y=2mx+1 và y=(m+1)x+m song song với nhau thì {2m=m+1m≠1⇒{m=1m≠1, do đó không có giá trị nào của m thỏa mãn bài toán.
Câu 32 :
Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng y=3x+1 và đi qua điểm (1;7)?
Đáp án : C Phương pháp giải :
Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng y=ax+b(a≠0) và y′=a′x+b′(a′≠0) song song với nhau khi a=a′,b≠b′ và ngược lại
Lời giải chi tiết :
Hàm số cần tìm có dạng y=3x+b(b≠1) Vì đường thẳng cần tìm đi qua điểm (1;7) nên ta có: 7=3.1+b, tìm được b=4 (thỏa mãn) Vậy hàm số cần tìm là y=3x+4
Câu 33 :
Hệ số góc của đường thẳng d biết d đi qua gốc tọa độ O và điểm M(2; 6) là:
Đáp án : C Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng y=ax+b(a≠0)
Lời giải chi tiết :
Gọi phương trình đường thẳng d cần tìm là y=ax+b(a≠0) Vì d đi qua gốc tọa độ nên b=0⇒y=ax Vì điểm M(2; 6) thuộc d nên 6=2a, a=3 (thỏa mãn) Phương trình đường thẳng d: y=3x nên hệ số góc của đường thẳng d là 3.
Câu 34 :
Đường thẳng y=2(m+1)x+m−2(m≠−1) đi qua điểm A(1; 9) có hệ số góc là:
Đáp án : B Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng y=ax+b(a≠0)
Lời giải chi tiết :
Vì điểm A(1; 9) thuộc đường thẳng y=2(m+1)x+m−2 nên: 9=2(m+1).1+m−2 3m=9 m=3 (thỏa mãn) Đường thẳng d: y=8x+1, do đó đường thẳng d có hệ số góc là 8
Câu 35 :
Cho hai đồ thị hàm số bậc nhất là hai đường thẳng d: y=(m−2)x−m và d′:y=−2x−2mx+3. Với giá trị nào của m thì d cắt d’
Đáp án : B Phương pháp giải :
Sử dụng nhận biết về hai đường thẳng cắt nhau: Hai đường thẳng y=ax+b(a≠0) và y′=a′x+b′(a′≠0) cắt nhau khi a≠a′ và ngược lại.
Lời giải chi tiết :
d là hàm số bậc nhất khi m≠2 d′:y=−2x−2mx+3=(−2−2m)x+3 d’ là hàm số bậc nhất khi m≠−1 Hai đường thẳng thẳng d: y=(m−2)x−m và d′:y=(−2−2m)x+3 cắt nhau thì: m−2≠−2−2m 3m≠0 m≠0 (thỏa mãn)
Câu 36 :
Cho hai đường thẳng d: y=(m+2)x+m và d’: y=−2x−2m+1. Với giá trị nào của m thì d trùng với d’?
Đáp án : A Phương pháp giải :
Sử dụng nhận biết về hai đường thẳng trùng nhau: Hai đường thẳng y=ax+b(a≠0) và y′=a′x+b′(a′≠0) trùng nhau khi a=a′,b=b′ và ngược lại
Lời giải chi tiết :
d là hàm số bậc nhất khi m≠−2 Hai đường thẳng d: y=(m+2)x+m và d’: y=−2x−2m+1 trùng nhau khi: {m+2=−2m=−2m+1⇔{m=−4m=13 (vô lí) Vậy không có giá trị nào của m thỏa mãn bài toán
Câu 37 :
Cho hàm số bậc nhất y=2ax+a−1 có đồ thị hàm số là đường d. Đường thẳng d có hệ số góc gấp hai lần hệ số góc của đường thẳng d’: y−4x+3=0 Khi đó, điểm A(x; 6) thuộc đường thẳng d thì giá trị của x là:
Đáp án : D Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng y=ax+b(a≠0)
Lời giải chi tiết :
Hàm số y=2ax+a−1 là hàm số bậc nhất khi a≠0 d’: y−4x+3=0, y=4x−3 Vì đường thẳng d có hệ số góc gấp hai lần hệ số góc của đường thẳng d’: y=4x−3 nên hệ số góc của đường thẳng d bằng 8, hay 2a=8, a=4 (thỏa mãn) Do đó, d: y=8x+3 Vì điểm A(x; 6) thuộc đường thẳng d nên 6=8.x+3 x=38
Câu 38 :
Hệ số góc của đường thẳng x3+y2=1 là:
Đáp án : C Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng y=ax+b(a≠0)
Lời giải chi tiết :
x3+y2=1 2x3+y=2 y=−2x3+2 Do đó, hệ số góc của đường thẳng trên là −23
Câu 39 :
Các điểm A(m; 3) và B(1; m) nằm trên đường thẳng có hệ số góc m>0. Tìm m.
Đáp án : D Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng y=ax+b(a≠0)
Lời giải chi tiết :
Đường thẳng có dạng y=mx+n (d) Vì đường thẳng d đi qua điểm A(m; 3) nên 3=m2+n (1) Vì đường thẳng d đi qua điểm B(1; m) nên m=m+n, tìm được n=0 Thay n=0 vào (1) ta có: m2=3, tìm được m=±√3 Mà m>0 nên m=√3
Câu 40 :
Cho hàm số bậc nhất y=mx+3 có đồ thị là đường thẳng d. Biết rằng đường thẳng d song song với đường thẳng y=−x. Gọi A là giao điểm của đường thẳng d với đồ thị của hàm số y=x+1. B là giao điểm của đường thẳng d với trục Ox. Diện tích tam giác OAB là:
Đáp án : C Phương pháp giải :
+ Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng y=ax+b(a≠0) và y′=a′x+b′(a′≠0) song song với nhau khi a=a′,b≠b′ và ngược lại + Đồ thị hàm số bậc nhất Lời giải chi tiết :
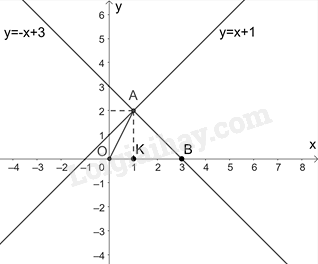
Hàm số y=mx+3 là hàm số bậc nhất khi m≠0 Vì đường thẳng d song song với đường thẳng y=−x nên m=−1 (thỏa mãn) Do đó, d: y=−x+3 Vẽ đồ thị của hai hàm số: y=−x+3 và y=x+1:
Nhìn vào đồ thị ta thấy, A(1; 2), B(3; 0), do đó, OB=3 Gọi K là hình chiếu của A trên trục Ox, do đó AK là đường cao trong tam giác OAB và AK=2 Diện tích tam giác OAB là: S=12AK.OB=12.3.2=3 (đvdt)
Câu 41 :
Cho hàm số bậc nhất y=12m2x+m10−m4−14mx+3(1) Tìm giá trị của m để đồ thị hàm số (1) có hệ số góc đạt giá trị nhỏ nhất.
Đáp án : B Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng y=ax+b(a≠0)
Lời giải chi tiết :
Ta có: y=12m2x+m10−m4−14mx+3=(12m2−14m)x+m10−m4+3 Hàm số (1) là hàm số bậc nhất khi 12m2−14m≠0, tìm được m≠0,m≠12 Ta có: 12m2−14m=12(m2−12m)=12(m2−2.m.14+116−116)=12(m−14)2−132≥−132 Do đó, hệ số góc của đồ thị hàm số (1) đạt giá trị nhỏ nhất là −132 khi m−14=0, m=14 (thỏa mãn)
|