Trắc nghiệm Bài 10: Hình đồng dạng trong thực tiễn Toán 8 Cánh diềuĐề bài
Câu 1 :
Cho hai tấm thảm hình tam giác ABC và A’B’C’, tấm thảm ABC có chu vi bằng 400cm và đồng dạng phối cảnh với tấm thảm A’B’C’ tâm O, tỉ số \(\frac{2}{3}.\) Chu vi tam giác A’B’C’ bằng:
Câu 2 :
Một tủ sách nghệ thuật ở có dạng như hình vẽ sau:
Trong đó BM, CN, DP, EQ là các ngăn của tủ sách và ngăn EQ có độ dài 4m. Có bao nhiêu khẳng định đúng trong các khẳng định sau? + Ngăn BM là hình đồng dạng phối cảnh với ngăn EQ, với tâm A, tỉ số bằng \(\frac{1}{4}\) + Ngăn CN là hình đồng dạng phối cảnh với ngăn DP, với tâm A, tỉ số bằng \(\frac{1}{3}\) + \(BM = 1m,CN = 2m,DP = 3m\)
Câu 3 :
: Cho hai bức tranh hình chữ nhật như hình vẽ sau đây:
Cho bức tranh A’B’C’D’ là hình đồng dạng của bức tranh ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 12cm,BC = 16cm,A'B' = 24cm.\) Khi đó, diện tích bức tranh A’B’C’D’ là:
Câu 4 :
Một chiếc khăn mặt có dạng hình tam giác ABC có \(AB = 12cm,BC = 16cm,AC = 20cm.\) Một chiếc khăn mặt khác hình tam giác A’B’C’ là hình đồng dạng phối cảnh của chiếc khăn ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Khăn tam giác A”B”C” là hình đồng dạng của khăn A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích chiếc khăn A”B”C” bằng \(1536c{m^2}\). Chọn đáp án đúng
Câu 5 :
Một mặt bàn hình chữ nhật ABCD có \(AB = \frac{5}{{12}}BC.\) Mặt bàn hình chữ nhật A’B’C’D’ là hình đồng dạng của mặt bàn hình chữ nhật ABCD có tỉ số đồng dạng 2. Biết rằng \(A'C' = 130cm.\) Khi đó, diện tích mặt bàn hình chữ nhật A’B’C’D’ bằng:
Câu 8 :
Trong các loài thực vật sau, loài thực vật nào thể hiện hình đồng dạng?
Câu 11 :
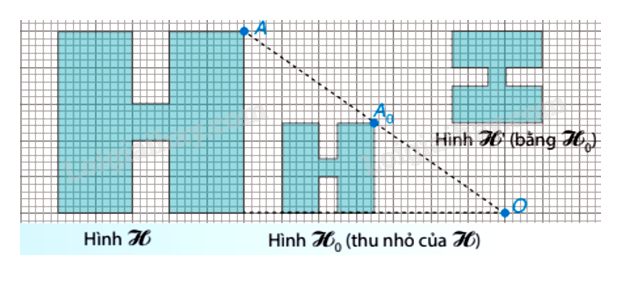
Cho hình vẽ:
Cho các khẳng định sau: + Hình H là hình đồng dạng phối cảnh của hình H 0 + Hình H ’ là hình đồng dạng phối cảnh của hình H 0 + Hình H đồng dạng của hình H 0 Có bao nhiêu khẳng định đúng?
Câu 13 :
Cho hai bức tranh như hình vẽ dưới đây:
Biết rằng bức tranh trong hình b là bức tranh trong hình a sau khi thu nhỏ với \(k = \frac{2}{3}.\) Nếu kích thước của bức tranh hình a là \(4 \times 6\) thì kích thước của bức tranh trong hình b là:
Câu 14 :
Hình bên dưới mô tả hai bức tranh kim tử tháp hình vuông những có kích thước khác nhau.
Biết rằng A, B, C, D lần lượt là trung điểm của OA’, OB’, OC’, OD’ Chọn đáp án đúng
Câu 15 :
Ba cái cây có hình vẽ như sau:
Cây 1 đồng dạng với cây 2 theo tỉ số là x. Để cây 2 đồng dạng với cây 3 theo tỉ số đồng dạng là x thì:
Câu 16 :
Cho hai tem thư hình vuông như hình vẽ dưới đây:
Biết rằng tem thư 1 có diện tích là \(144c{m^2}\), tem thư 2 có chu vi là 40cm Chọn đáp án đúng
Câu 17 :
Hình ảnh bên dưới là bức tranh Đông Hồ (hình chữ nhật) nhưng có kích thước khác nhau.
Biết rằng B, C, A, D lần lượt là trung điểm của OF, OG, OE, OH và diện tích của bức tranh ABCD bằng \(100c{m^2}\). Diện tích của bức tranh EFGH là:
Câu 18 :
Hai cái đĩa có mặt đĩa là hình tròn như hình sau:
Biết rằng mặt đĩa H có diện tích bằng \(113,04c{m^2}\). Mặt đĩa H’ là hình đồng dạng với mặt đĩa H có tỉ số đồng dạng bằng \(2\). Khi đó, diện tích của mặt đĩa H’ bằng:
Lời giải và đáp án
Câu 1 :
Cho hai tấm thảm hình tam giác ABC và A’B’C’, tấm thảm ABC có chu vi bằng 400cm và đồng dạng phối cảnh với tấm thảm A’B’C’ tâm O, tỉ số \(\frac{2}{3}.\) Chu vi tam giác A’B’C’ bằng:
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh. + Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\) Lời giải chi tiết :
Chu vi tấm thảm ABC là: \(AB + BC + AC = 400\) Chu vi tấm thảm A’B’C’ là: \(P' = A'B' + B'C' + A'C'\) Vì tấm thảm ABC đồng dạng phối cảnh với tấm thảm A’B’C’ tâm O, tỉ số \(\frac{2}{3}\) nên ta có: \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}} = \frac{2}{3}\) Theo tính chất của dãy tỉ số bằng nhau ta có: \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}} = \frac{{AB + BC + AC}}{{A'B' + B'C' + A'C'}} = \frac{{400}}{{P'}} = \frac{2}{3}\) nên \(P' = 400.\frac{3}{2} = 600\left( {cm} \right)\)
Câu 2 :
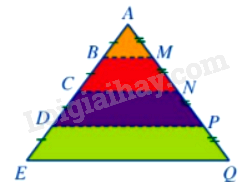
Một tủ sách nghệ thuật ở có dạng như hình vẽ sau:
Trong đó BM, CN, DP, EQ là các ngăn của tủ sách và ngăn EQ có độ dài 4m. Có bao nhiêu khẳng định đúng trong các khẳng định sau? + Ngăn BM là hình đồng dạng phối cảnh với ngăn EQ, với tâm A, tỉ số bằng \(\frac{1}{4}\) + Ngăn CN là hình đồng dạng phối cảnh với ngăn DP, với tâm A, tỉ số bằng \(\frac{1}{3}\) + \(BM = 1m,CN = 2m,DP = 3m\)
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh. + Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\) Lời giải chi tiết :
Vì \(\frac{{AM}}{{AQ}} = \frac{{AB}}{{AE}}\left( { = \frac{1}{4}} \right)\) và các đường thẳng BE và MQ cắt nhau tại A nên BM là hình đồng dạng phối cảnh với EQ, tâm A, tỉ số đồng dạng \(\frac{1}{4}\) Vì \(\frac{{AC}}{{AD}} = \frac{{AN}}{{AP}}\left( { = \frac{2}{3}} \right)\) và các đường thẳng DC và NP cắt nhau tại A nên CN là hình đồng dạng phối cảnh với DP, tâm A, tỉ số đồng dạng \(\frac{2}{3}\) Trong tam giác AQE có: \(\frac{{AM}}{{AQ}} = \frac{{AB}}{{AE}}\left( { = \frac{1}{4}} \right)\) nên BM//EQ. Áp dụng hệ quả định lý Thalès vào tam giác AQE có: \(\frac{{BM}}{{EQ}} = \frac{{AB}}{{AE}} \Rightarrow \frac{{BM}}{4} = \frac{1}{4} \Rightarrow BM = 1\left( m \right)\) Trong tam giác AQE có: \(\frac{{AD}}{{AE}} = \frac{{AP}}{{AQ}}\left( { = \frac{3}{4}} \right)\) nên DP//EQ. Theo hệ quả định lý Thalès vào tam giác AQE có: \(\frac{{PD}}{{EQ}} = \frac{{AP}}{{AQ}} \Rightarrow \frac{{DP}}{4} = \frac{3}{4} \Rightarrow DP = 3\left( m \right)\) Trong tam giác ADP có: \(\frac{{AC}}{{AD}} = \frac{{AN}}{{AP}}\left( { = \frac{2}{3}} \right)\) nên CN//DP. Theo hệ quả định lý Thalès vào tam giác APD có: \(\frac{{CN}}{{DP}} = \frac{{AC}}{{AD}} \Rightarrow \frac{{CN}}{3} = \frac{2}{3} \Rightarrow CN = 2\left( m \right)\) Vậy có 2 khẳng định đúng
Câu 3 :
: Cho hai bức tranh hình chữ nhật như hình vẽ sau đây:
Cho bức tranh A’B’C’D’ là hình đồng dạng của bức tranh ABCD với tỉ số đồng dạng k. Biết rằng \(AB = 12cm,BC = 16cm,A'B' = 24cm.\) Khi đó, diện tích bức tranh A’B’C’D’ là:
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’ + Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H Lời giải chi tiết :
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD với tỉ số đồng dạng k nên \(k = \frac{{A'B'}}{{AB}} = \frac{{24}}{{12}} = 2\) Ta có: \(\frac{{B'C'}}{{BC}} = 2 \Rightarrow B'C' = 16.2 = 32\left( {cm} \right)\) Diện tích bức tranh A’B’C’D’ là: \(A'B'.B'C' = 24.32 = 768\left( {c{m^2}} \right)\)
Câu 4 :
Một chiếc khăn mặt có dạng hình tam giác ABC có \(AB = 12cm,BC = 16cm,AC = 20cm.\) Một chiếc khăn mặt khác hình tam giác A’B’C’ là hình đồng dạng phối cảnh của chiếc khăn ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2. Khăn tam giác A”B”C” là hình đồng dạng của khăn A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x \(\left( {x > 0} \right)\). Diện tích chiếc khăn A”B”C” bằng \(1536c{m^2}\). Chọn đáp án đúng
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh. + Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\) Lời giải chi tiết :
Vì tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC, O là tâm đồng dạng phối cảnh, tỉ số vị tự là 2 nên \(\Delta A'B'C'\backsim \Delta ABC\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=2\) \(\Rightarrow A'B'=24cm,B'C'=32cm,A'C'=40cm\) Vì \(A'C{{'}^{2}}=A'B{{'}^{2}}+B'C{{'}^{2}}\left( {{40}^{2}}={{32}^{2}}+{{24}^{2}} \right)\) nên tam giác A’B’C’ vuông tại B’ Vì tam giác A”B”C” là hình đồng dạng của tam giác A’B’C’, O là tâm đồng dạng phối cảnh, tỉ số vị tự là x nên \(\Delta A''B''C''\backsim \Delta A'B'C'\) Do đó, \(\widehat{A''B''C''}=\widehat{A'B'C'}=90\) và \(\frac{A''B''}{A'B'}=\frac{A''C''}{A'C'}=\frac{B''C''}{B'C'}=x\Rightarrow A''B''=24x,A''C''=40x,B''C''=32x\) Vì tam giác A”B”C” vuông tại B” nên diện tích tam giác A”B”C” là: \({{S}_{A''B''C''}}=\frac{1}{2}B''A''.B''C''\Rightarrow \frac{1}{2}.24x.32x=1536\Rightarrow {{x}^{2}}=4\Rightarrow x=2\)(do \(x>0\))
Câu 5 :
Một mặt bàn hình chữ nhật ABCD có \(AB = \frac{5}{{12}}BC.\) Mặt bàn hình chữ nhật A’B’C’D’ là hình đồng dạng của mặt bàn hình chữ nhật ABCD có tỉ số đồng dạng 2. Biết rằng \(A'C' = 130cm.\) Khi đó, diện tích mặt bàn hình chữ nhật A’B’C’D’ bằng:
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’ + Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H Lời giải chi tiết :
Vì hình chữ nhật A’B’C’D’ là hình đồng dạng của hình chữ nhật ABCD có tỉ số đồng dạng 2 nên \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = 2\) Mà \(AB = \frac{5}{{12}}BC \Rightarrow A'B' = \frac{5}{{12}}B'C'.\) Vì A’B’C’D’ là hình chữ nhật nên \(\widehat {A'B'C'} = {90^0}\) Do đó, tam giác A’B’C’ vuông tại B’. Áp dụng định lý Pytago vào tam giác A’B’C’ vuông tại B’ ta có: \(A'C{'^2} = A'B{'^2} + B'C{'^2}\) (1) Thay \(A'B' = \frac{5}{{12}}B'C'\) vào (1) ta có: \({\left( {\frac{5}{{12}}B'C'} \right)^2} + B'C{'^2} = {130^2}\) \(\frac{{169}}{{144}}B'C{'^2} = 16900\) \(B'C{'^2} = 14400\) nên \(B'C' = 120cm\) Do đó, \(A'B' = \frac{5}{{12}}.120 = 50\left( {cm} \right)\) Vậy diện tích hình chữ nhật A’B’C’D’ là: \(A'B'.B'C' = 50.120 = 6000\left( {c{m^2}} \right)\)
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về hai hình đồng dạng: Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Lời giải chi tiết :
Các hình a, b, c đều thể hiện hình đồng dạng, chỉ có hình d là không thể hiện hình đồng dạng.
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về hai hình đồng dạng: Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H
Lời giải chi tiết :
Trong các hình trên, chỉ có hình cánh hoa ở đáp án B là hình đồng dạng với hình cánh hoa đề bài cho
Câu 8 :
Trong các loài thực vật sau, loài thực vật nào thể hiện hình đồng dạng?
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H ’được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’ + Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H Lời giải chi tiết :
Cả ba loài thực vật trong đáp án A, B, C đều thể hiện hình đồng dạng.
Đáp án : C Phương pháp giải :
Lời giải chi tiết :
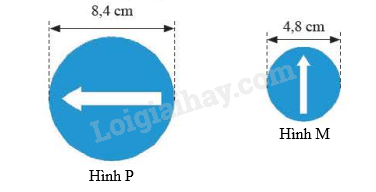
Ta có: \(k = \frac{{4,8}}{{8,4}} = \frac{4}{7}\) nên biển báo M là hình đồng dạng của biển báo P khi thu nhỏ với tỉ số \(k = \frac{4}{7}\)
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về hai hình đồng dạng:
+ Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H Lời giải chi tiết :
Các cặp hình đồng dạng là: Hình a và hình c, hình b và hình d. Vậy có 2 cặp hình đồng dạng.
Câu 11 :
Cho hình vẽ:
Cho các khẳng định sau: + Hình H là hình đồng dạng phối cảnh của hình H 0 + Hình H ’ là hình đồng dạng phối cảnh của hình H 0 + Hình H đồng dạng của hình H 0 Có bao nhiêu khẳng định đúng?
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh. + Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\) Sử dụng kiến thức về hai hình đồng dạng: + Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’ + Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H - Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng Lời giải chi tiết :
Hình H là hình đồng dạng phối cảnh của hình H 0 Mà hình H ’ bằng với hình H 0 nên hình H đồng dạng của hình H 0 Vì hình H là hình đồng dạng phối cảnh của hình H 0 nên H là hình đồng dạng của hình H 0 Vậy cả ba khẳng định trên đều đúng
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’ + Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H Lời giải chi tiết :
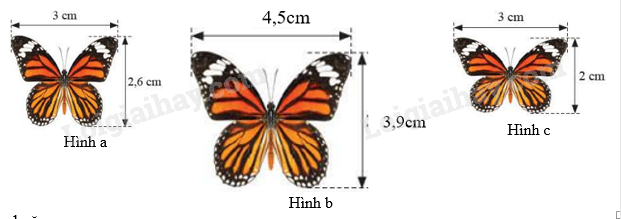
Vì \(\frac{{4,5}}{3} = \frac{{3,9}}{{2,6}}\left( { = \frac{3}{2}} \right)\) nên hình b đồng dạng với hình a với tỉ số \(\frac{3}{2}\) Vì \(\frac{{4,5}}{3} \ne \frac{{3,9}}{2}\) nên hai hình b và c không đồng dạng với nhau Vì \(\frac{3}{3} \ne \frac{2}{{2,6}}\) nên hai hình a và c không đồng dạng với nhau
Câu 13 :
Cho hai bức tranh như hình vẽ dưới đây:
Biết rằng bức tranh trong hình b là bức tranh trong hình a sau khi thu nhỏ với \(k = \frac{2}{3}.\) Nếu kích thước của bức tranh hình a là \(4 \times 6\) thì kích thước của bức tranh trong hình b là:
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’ + Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H Lời giải chi tiết :
Vì rằng bức tranh trong hình b là bức tranh trong hình a sau khi thu nhỏ với \(k = \frac{2}{3}\) nên kích thước ở hình b là: \(4.\frac{2}{3} = \frac{8}{3}\) và \(6.\frac{2}{3} = 4\) Vậy kích thước của bức tranh trong hình b là: \(\frac{8}{3} \times 4\)
Câu 14 :
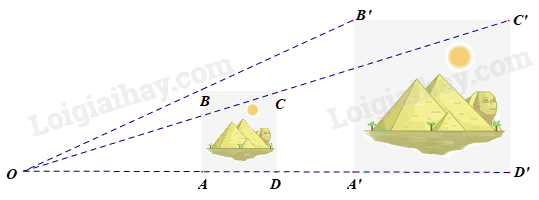
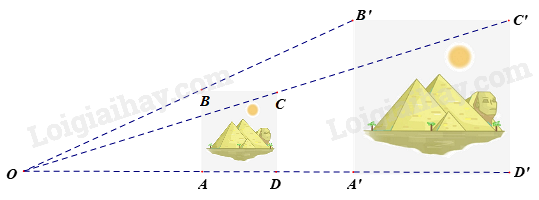
Hình bên dưới mô tả hai bức tranh kim tử tháp hình vuông những có kích thước khác nhau.
Biết rằng A, B, C, D lần lượt là trung điểm của OA’, OB’, OC’, OD’ Chọn đáp án đúng
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh. + Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\) Lời giải chi tiết :
Vì A, B, C, D lần lượt là trung điểm của OA’, OB’, OC’, OD’ nên \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = \frac{{OD'}}{{OD}} = 2\) Lại có các đường thẳng AA’, BB’, CC’, DD’ cùng đi qua điểm O. Do đó, bức tranh A’B’C’D’ là hình đồng dạng phối cảnh của bức tranh ABCD, tâm đồng dạng phối cảnh là điểm O, tỉ số 2
Câu 15 :
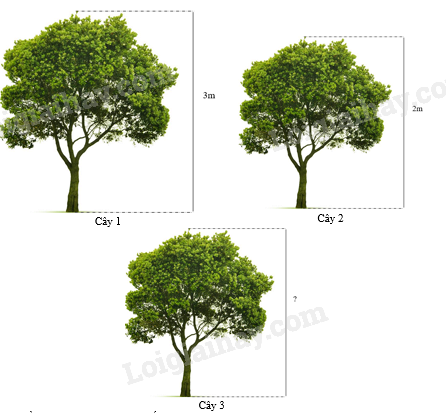
Ba cái cây có hình vẽ như sau:
Cây 1 đồng dạng với cây 2 theo tỉ số là x. Để cây 2 đồng dạng với cây 3 theo tỉ số đồng dạng là x thì:
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’ + Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H Lời giải chi tiết :
Cây 1 đồng dạng với cây 2 theo tỉ số là \(x = \frac{3}{2}\) Để cây 2 đồng dạng với cây 3 theo tỉ số đồng dạng là \(\frac{3}{2}\) thì \(? = 2:\frac{3}{2} = \frac{4}{3}\left( m \right)\)
Câu 16 :
Cho hai tem thư hình vuông như hình vẽ dưới đây:
Biết rằng tem thư 1 có diện tích là \(144c{m^2}\), tem thư 2 có chu vi là 40cm Chọn đáp án đúng
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’ + Hình H đồng dạng với hình H’ nếu hình H’ bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H Lời giải chi tiết :
Độ dài cạnh của tem thư 1 là: \(\sqrt {144} = 12\left( {cm} \right)\) Độ dài cạnh của tem thư 2 là: \(40:4 = 10\left( {cm} \right)\) Do đó, tem thư 1 là hình đồng dạng với tem thư 2 với tỉ số: \(\frac{{12}}{{10}} = \frac{6}{5}\)
Câu 17 :
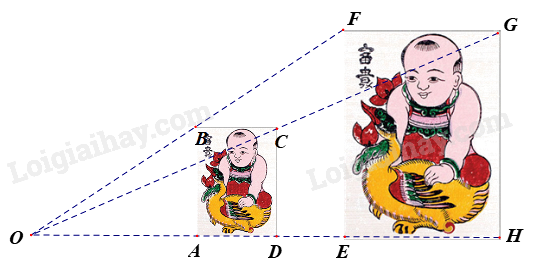
Hình ảnh bên dưới là bức tranh Đông Hồ (hình chữ nhật) nhưng có kích thước khác nhau.
Biết rằng B, C, A, D lần lượt là trung điểm của OF, OG, OE, OH và diện tích của bức tranh ABCD bằng \(100c{m^2}\). Diện tích của bức tranh EFGH là:
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự):
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh. + Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\) Lời giải chi tiết :
Vì B, C, A, D lần lượt là trung điểm của OF, OG, OE, OH nên \(\frac{{OB}}{{FO}} = \frac{{OA}}{{OE}} = \frac{{OD}}{{OH}} = \frac{{OC}}{{OG}} = \frac{1}{2}\) và các đường thẳng AD, EH, GC, FB cùng đi qua điểm O nên hình ABCD là hình đồng dạng phối cảnh với hình EFGH tâm O tỉ số \(\frac{1}{2}\). Do đó, \(FG = 2BC,FE = 2AB\) Diện tích bức tranh ABCD là: \(AB.BC = 100\left( {c{m^2}} \right)\) Diện tích bức tranh EFGH là: \(FE.FG = 2AB.2BC = 4AB.BC = 4.100 = 400\left( {c{m^2}} \right)\)
Câu 18 :
Hai cái đĩa có mặt đĩa là hình tròn như hình sau:
Biết rằng mặt đĩa H có diện tích bằng \(113,04c{m^2}\). Mặt đĩa H’ là hình đồng dạng với mặt đĩa H có tỉ số đồng dạng bằng \(2\). Khi đó, diện tích của mặt đĩa H’ bằng:
Đáp án : D Phương pháp giải :
Sử dụng kiến thức về hai hình đồng dạng:
+ Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’ + Hình H đồng dạng với hình H’ nếu hình H’ bằng hình H hoặc bằng một hình phóng to hoặc thu nhỏ của H Lời giải chi tiết :
Vì mặt đĩa H có diện tích bằng \(113,04c{m^2}\) nên bán kính của mặt đĩa H là: \({R^2} = \frac{{113,04}}{{3,14}} = 36 \Rightarrow R = 6cm\) Vì mặt đĩa H’ là hình đồng dạng với mặt đĩa H có tỉ số đồng dạng bằng 2 nên bán kính mặt đĩa H’ là: \(R' = 2R = 12\left( {cm} \right)\) Diện tích mặt đĩa H’ là: \({12^2}.3,14 = 452,16\left( {c{m^2}} \right)\)
|