Nội dung từ Loigiaihay.Com
Cho đường thẳng y=mx+m+1(1) (m là tham số). Đường thẳng (1) luôn đi qua một điểm cố định mới mọi giá trị của m. Điểm cố định đó là:
-
A.
(1; -1)
-
B.
(1; 1)
-
C.
(-1; -1)
-
D.
(-1; 1)
Do đó, y0=f(x0;m) có nghiệm đúng với mọi m.
Gọi điểm N(x0;y0) là điểm cố định của đường thẳng (1).
Ta có: y0=mx0+m+1
y0−mx0−m−1=0
−(x0+1)m+y0−1=0
Để phương trình luôn đúng với mọi m thì {x0+1=0y0−1=0
Suy ra {x0=−1y0=1
Vậy đường thẳng (1) luôn đi qua điểm cố định (-1; 1).
Đáp án : D

Các bài tập cùng chuyên đề
Trong các hình vẽ dưới đây, hình vẽ nào là đồ thị của hàm số y=1+2x?
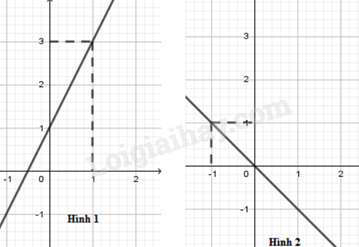
Cho đồ thị hàm số y=x+1. Điểm nào dưới đây thuộc đồ thị hàm số trên?
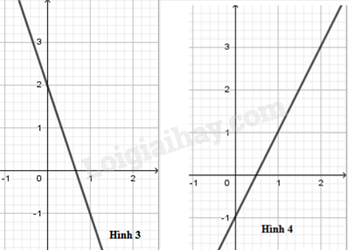
Một người đi bộ trên đường thẳng với vận tốc v (km/h). Gọi s (km) là quãng đường đi được trong t (giờ). Khi đó, đồ thị của hàm số s theo biến t với v=5 đường thẳng nào trong hình vẽ dưới đây?
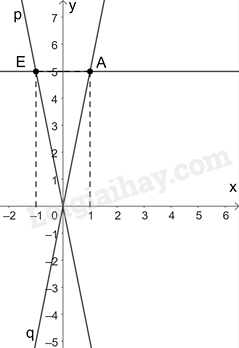
Cho đường thẳng d: y=2x+m. Đường thẳng d đi qua điểm A(1; 5). Chọn đáp án đúng.
Cho hàm số bậc nhất y=(2−m)x+m. Xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ 4.
Đồ thị của hàm số y=ax+b(a≠0) là:
Đồ thị hàm số y=ax+b(a≠0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng:
Cho hai đường thẳng d1:y=x−1 và d2:y=3−4x. Tung độ giao điểm của hai đường thẳng d1 và d2 là:
Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ: y=x;y=x+2;y=−x+2;y=−x. Bốn đồ thị nói trên cắt nhau tại các điểm O(0; 0), A, B, C. Tứ giác có 4 đỉnh O, A, B, C là hình gì?
Cho hàm số y=mx+2 có đồ thị là đường thẳng d1 và hàm số y=12x+1 có đồ thị là đường thẳng d2. Để đường thẳng d1 và đường thẳng d2 cắt nhau tại một điểm có hoành độ bằng 4 là:
Cho hàm số y=(m−1)x−1 có đồ thị là đường thẳng d1 và hàm số y=x+1 có đồ thị là đường thẳng d2. Để đường thẳng d1 và đường thẳng d2 cắt nhau tại một điểm có tung độ bằng 4 là:
Cho đường thẳng d1:y=−x+3 và d2:y=4−3x. Gọi A và B lần lượt là giao điểm của d1 và d2 với trục hoành. Tổng hoành độ giao điểm của hai điểm A và B là:
Cho đường thẳng d: y=−2x−4. Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Diện tích tam giác OAB là:
Với giá trị nào của m thì ba đường thẳng d1:y=(m−1)x−3;d2:y=2x+1;d3:y=x−3 giao nhau tại một điểm?
Gọi d1 là đồ thị của hàm số y=mx−1 và d2 là đồ thị hàm số y=12x+2. Để M(2; 3) là giao điểm của d1 và d2 thì giá trị của m là:
Cho đường thẳng d được xác định bởi y=2x+10. Đường thẳng d’ đối xứng với đường thẳng d qua trục hoành là:
Cho đường thẳng d xác định bởi y=2x+4. Đường thẳng d’ đối xứng với đường thẳng d qua đường thẳng y=x là:
Tìm x sao cho ba điểm A(x; 14), B(-5; 20), C(7; -16) thẳng hàng.
Có bao nhiêu đường thẳng đi qua A(4; 3), cắt trục tung tại điểm có tung độ là một số nguyên dương, cắt trục hoành tại điểm có hoành độ làm một số nguyên tố.
Hệ số góc của đường thẳng y=2x+1 là:












