Đề thi vào lớp 6 môn Toán trường Nguyễn Tất Thành năm 2024 (Mã đề 602)Tải vềKết quả phép tính
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
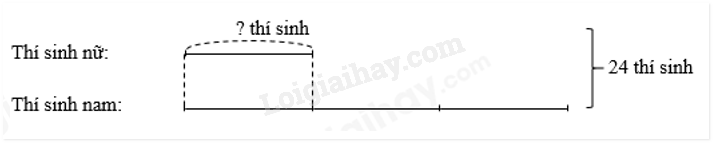
Đề thi ĐỀ TUYỂN SINH LỚP 6 TRƯỜNG THCS VÀ THPT NGUYỄN TẤT THÀNH NĂM HỌC 2024 - 2025 Môn: TOÁN Thời gian làm bài: 45 phút Mã đề 602 I. TRẮC NGHIỆM (Khoanh vào chữ cái trước đáp án đúng từ Câu 1 đến Câu 6) Câu 1. Kết quả phép tính \(12,7 \times 5 + 12,7 \times 95\) bằng: A. 172 B. 1270 C. 12,7 D. 127 Câu 2. Sau khi kiểm tra 1000 sản phẩm xuất xưởng, người ta nhận thấy có 9 sản phẩm bị lỗi. Tỉ số phần trăm của số sản phẩm bị lỗi và số sản phẩm đã được kiểm tra là A. 0,9% B. 0,09% C. 90% D. 9% Câu 3. Trong phòng thi có 24 thí sinh. Biết \(\frac{1}{3}\) số thí sinh nam bằng số thí sinh nữ. Số thí sinh nam trong phòng thi đó là A. 8 B. 24 C. 6 D. 4 Câu 4. Tại nhà bóng của một khu vui chơi, các nhân viên đã thống kê số lượng bóng theo màu của 1000 quả bóng và vẽ được biểu đồ sau:
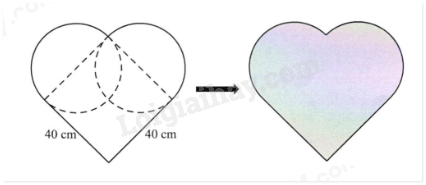
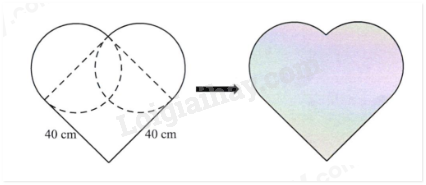
Số lượng bóng màu đỏ trong số 1000 quả bóng đó là A. 150 quả B. 250 quả C. 200 quả D. 400 quả Câu 5. Một cái bể nước có lòng bể dạng hình hộp chữ nhật có chiều dài bằng 2m; chiều rộng bằng 1m và chiều cao bằng \(\frac{1}{2}\) chiều dài. Hiện tại, bể đang chứa 1300 lít nước. Để vừa đầy bể, cần bơm thêm số lít nước nữa là A. 2 lít B. 2000 lít. C. 1298 lít. D. 700 lít. Câu 6. Bạn Hòa vẽ một hình trái tim bằng cách sau: vẽ một hình vuông cạnh 40 cm, sau đó vẽ hai đường tròn có đường kính lần lượt là hai cạnh kể nhau của hình vuông, rồi tô màu (xem hình minh họa dưới đây).
Diện tích hình trái tim đó là A. 1600cm2. B. 1000cm2. C. 5024cm2. D. 2856cm2. II. TRẢ LỜI NGẮN (Viết đáp số của bài toán vào ô trống từ Câu 7 đến Câu 10)
III. TỰ LUẬN (Trình bày chi tiết lời giải Câu 11 và Câu 12) Câu 11. Đầu năm học, câu lạc bộ “Em yêu Toán" có 30 học sinh nữ và chiếm 60% tổng số học sinh của câu lạc bộ đó. 1. Tính số học sinh nam của câu lạc bộ “Em yêu Toán”. 2. Hết học kì I, câu lạc bộ “Em yêu Toán” không có học sinh nào chuyển đi mà có một số học sinh nữ và một số học sinh nam từ các câu lạc bộ khác cùng chuyển sang câu lạc bộ này. Số học sinh nam và số học sinh nữ chuyển đến như nhau. Khi đó, số học sinh nữ bằng 140% số học sinh nam. Tính số học sinh nữ đã chuyển đến. Câu 12. Cho hình thang ABCD (AB và CD là hai cạnh đáy), CD = 2 × AB. Trên đoạn thẳng AC lấy điểm M sao cho AM = MC. Trên đoạn thẳng DM lấy điểm N sao cho MN = 2× DN. Kéo dài AN cắt DC tại P. Biết diện tích hình tam giác ABC bằng 60cm. 1. Tính diện tích hình thang ABCD. 2. Tính diện tích tam giác DN.
Đáp án HƯỚNG DẪN GIẢI CHI TIẾT I. TRẮC NGHIỆM (Khoanh vào chữ cái trước đáp án đúng từ Câu 1 đến Câu 6) Câu 1. Kết quả phép tính \(12,7 \times 5 + 12,7 \times 95\)bằng: A. 172 B. 1270 C. 12,7 D. 127 Lời giải \(12,7 \times 5 + 12,7 \times 95 = 12,7 \times (95 + 5)\) = \(12,7 \times 100\) \( = 1270\) Chọn B Câu 2. Sau khi kiểm tra 1000 sản phẩm xuất xưởng, người ta nhận thấy có 9 sản phẩm bị lỗi. Tỉ số phần trăm của số sản phẩm bị lỗi và số sản phẩm đã được kiểm tra là A. 0,9% B. 0,09% C. 90% D. 9% Lời giải: Tỉ số phần trăm của số sản phẩm bị lỗi và số sản phẩm đã được kiểm tra là: \(9 \div 1000 \times 100 = 0,9\% \) Chọn A Câu 3. Trong phòng thi có 24 thí sinh. Biết \(\frac{1}{3}\) số thí sinh nam bằng số thí sinh nữ. Số thí sinh nam trong phòng thi đó là A. 8 B. 24 C. 6 D. 4 Lời giải:
Tổng số phần bằng nhau là: \(1 + 3 = 4\) (phần) Số thí sinh nam trong phòng thi đó là: \(24 \div 4 \times 1 = 6\)(thí sinh) Chọn C Câu 4. Tại nhà bóng của một khu vui chơi, các nhân viên đã thống kê số lượng bóng theo màu của 1000 quả bóng và vẽ được biểu đồ sau:
Số lượng bóng màu đỏ trong số 1000 quả bóng đó là A. 150 quả B. 250 quả C. 200 quả D. 400 quả Lời giải: Số bóng màu đỏ chiếm số phần trăm trong số 1000 quả bóng là: \(100\% {\rm{ }} - {\rm{ }}25\% {\rm{ }} - {\rm{ }}40\% {\rm{ }} - {\rm{ 20}}\% {\rm{ }} = {\rm{ 15}}\% \) Số lượng bóng màu đỏ là: \(1000 \div 100 \times 15 = 150\) (quả) Chọn A Câu 5. Một cái bể nước có lòng bể dạng hình hộp chữ nhật có chiều dài bằng 2m; chiều rộng bằng 1m và chiều cao bằng \(\frac{1}{2}\) chiều dài. Hiện tại, bể đang chứa 1300 lít nước. Để vừa đầy bể, cần bơm thêm số lít nước nữa là A. 2 lít B. 2000 lít. C. 1298 lít. D. 700 lít. Lời giải: Chiều cao của bể nước là: \(2 \times \frac{1}{2} = 1\)(m) Thể tích của bể nước là: \(2 \times 1 \times 1 = 2\)(m3) Đổi 1m3 = 1000 dm3 = 1000 lít Để vừa đầy bể, cần bơm thêm số lít nước là: \(1000--1300{\rm{ }} = 700\) (lít) Chọn D Câu 6. Bạn Hòa vẽ một hình trái tim bằng cách sau: vẽ một hình vuông cạnh 40 cm, sau đó vẽ hai đường tròn có đường kính lần lượt là hai cạnh kể nhau của hình vuông, rồi tô màu (xem hình minh họa dưới đây).
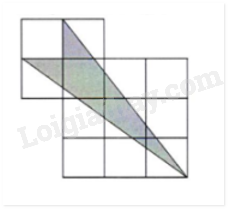
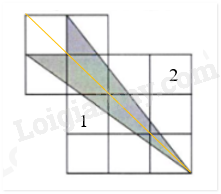
Diện tích hình trái tim đó là A. 1600cm2. B. 1000cm2. C. 5024cm2. D. 2856cm2. Lời giải Hai nửa hình tròn tạo thành một hình tròn hoàn chỉnh có đường kính dài 40 cm. Bán kính của hình tròn là: \(40 \div 2 = 20\) (cm) Diện tích hình tròn là: \(20 \times 20 \times 3,14 = 1256\) (cm2) Diện tích hình vuông là: \(40 \times 40 = 1600\) (cm2) Diện tích hình trái tim là: \(1256 + 1600 = 2856\) (cm2) Chọn D II. TRẢ LỜI NGẮN (Viết đáp số của bài toán vào ô trống từ Câu 7 đến Câu 10) Câu 7. Hiện nay, tổng số tuổi của hai anh em là 25 tuổi. Biết số tuổi của anh hơn số tuổi của em là 5 tuổi. Tính số tuổi của anh hiện nay. Lời giải Số tuổi của anh hiện nay là: \((25 - 5) \div 3 = 15\) (tuổi) Đáp số: 8 tuổi Câu 8. Một đội có 12 người thì hoàn thành công việc được giao trong 10 ngày. Hỏi nếu đội có 15 người thì sẽ hoàn thành công việc đó trong bao nhiêu ngày? (Năng suất của mỗi người là như nhau) Lời giải 1 người hoàn thành công việc trong số ngày là: \(10 \times 12 = 120\) (ngày) 15 người hoàn thành công việc trong số ngày là: \(120 \div 15 = 8\) (ngày) Đáp số: 30 ngày Câu 9. Một ô tô chở học sinh lớp 6A của Trường THCS & THPT Nguyễn Tất Thành đi dã ngoại xuất phát từ trường lúc 6 giờ 30 phút với vận tốc 60 km/giờ. Khi đến khu dã ngoại, học sinh tham gia các hoạt động trải nghiệm trong 3 giờ. Sau đó, ô tô chở học sinh quay về với vận tốc 45 km/giờ và về đến trường lúc 10 giờ 40 phút cùng ngày. Biết quãng đường đi và quãng đường về bằng nhau. Tính quãng đường từ trường đến khu dã ngoại. Lời giải Tổng thời gian di chuyển từ trường tới khu dã ngoại và trở về trường của lớp 6A là: 10 giờ 40 phút \( - \) 6 giờ 30 phút \( - \) 3 giờ \( = \) 1 giờ 10 phút Đổi 1 giờ 10 phút \( = \)\(\frac{7}{6}\) giờ Tỉ số vận tốc lúc đi và vận tốc lúc về là: \(\frac{{60}}{{45}} = \frac{4}{3}\) Trên cùng một quãng đường, thời gian và vận tốc là hai đại lượng tỉ lệ nghịch với nhau. Vậy tỉ số thời gian lúc đi và thời gian lúc về là: \(\frac{3}{4}\) Thời gian lúc đi là: \(\frac{7}{6}:(3 + 4) \times 3 = 0,5\) (giờ) Độ dài quãng đường từ trường đến khu dã ngoại là: \(60 \times 0,5 = 30\) (km) Đáp số: 30 km Câu 10. Cho hình minh họa bên. Biết có tất cả 12 hình vuông nhỏ, mỗi hình vuông nhỏ có diện tích là 25cm2. Tính diện tích của phần tô màu đậm theo đơn vị xăng-ti-mét vuông.
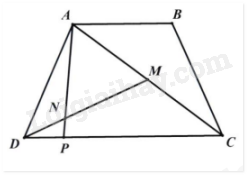
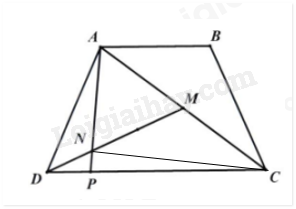
Lời giải: Hình vẽ trên gồm 12 hình vuông nhỏ có diện tích 25cm2. Ta thấy hình số 1 và hình số 2, mỗi hình bao gồm 1,5 hình vuông được tô đậm. Số hình vuông được tô đậm là: \(1,5 + 1,5 = 3\)(hình vuông) Diện tích phần được tô đậm là: \(25 \times 3 = 75\) (cm2) Đáp số: 75cm2 III. TỰ LUẬN (Trình bày chi tiết lời giải Câu 11 và Câu 12) Câu 11. Đầu năm học, câu lạc bộ “Em yêu Toán" có 30 học sinh nữ và chiếm 60% tổng số học sinh của câu lạc bộ đó. 1. Tính số học sinh nam của câu lạc bộ “Em yêu Toán”. 2. Hết học kì I, câu lạc bộ “Em yêu Toán” không có học sinh nào chuyển đi mà có một số học sinh nữ và một số học sinh nam từ các câu lạc bộ khác cùng chuyển sang câu lạc bộ này. Số học sinh nam và số học sinh nữ chuyển đến như nhau. Khi đó, số học sinh nữ bằng 140% số học sinh nam. Tính số học sinh nữ đã chuyển đến. Lời giải: 1. Tổng số học sinh của câu lạc bộ là: \(30 \times 100 \div 60 = 50\) (học sinh) Số học sinh nam của câu lạc bộ là: \(50 - 30 = 20\) (học sinh) 2. Ban đầu, hiệu số học sinh nữ và số học sinh nam là: \(30 - 20 = 10\) (học sinh) Vì số học sinh nữ và số học sinh nam chuyển đến như nhau nên hiệu số học sinh nữ và số học nam không thay đổi. Đổi \(140\% = \frac{7}{5}\), số học sinh bằng \(\frac{7}{5}\) số học sinh nam. Số học sinh nữ lúc sau là: \(10 - (7 - 5) \times 7 = 35\) (học sinh) Số học sinh nữ đã chuyển đến là: \(35 - 30 = 5\) (học sinh) Đáp số: a) 20 học sinh b) 5 học sinh Câu 12. Cho hình thang ABCD (AB và CD là hai cạnh đáy), \(CD = 2 \times AB\). Trên đoạn thẳng AC lấy điểm M sao cho AM = MC. Trên đoạn thẳng DM lấy điểm N sao cho \(MN = 2 \times DN\). Kéo dài AN cắt DC tại P. Biết diện tích hình tam giác ABC bằng 60cm. 1. Tính diện tích hình thang ABCD. 2. Tính diện tích tam giác DNP.
Lời giải 1. Vì AB song song với CD nên hai tam giác ABC và ADC có chiều cao bằng nhau. SADC = \({S_{ADC}} = 2 \times {S_{ABC}} = 2 \times 60 = 120\)(cm2) (Vì \(CD = 2 \times AB\) và chiều cao bằng nhau). Do đó, \({S_{ABCD}} = {S_{ABC}} + {S_{ADC}} = 60 + 120 = 180\) (cm2) 2.
Nối điểm N với điểm C. Ta có \({S_{DAM}} = {S_{DCM}} = \frac{1}{2} \times {S_{ADC}} = \frac{1}{2} \times 120 = 60\) (cm2) (Vì \(MN = 2 \times DN\) và chung chiều cao hạ từ D xuống AC). \({S_{DAN}} = \frac{1}{3} \times {S_{DAM}} = \frac{1}{3} \times 60 = 20\) (cm2) (Vì \(MN = 2 \times DN\)nên \(DN = \frac{1}{3} \times DM\) và chung chiều cao hạ từ A xuống DM). Suy ra, \({S_{NAM}} = {S_{DAM}} - {S_{DAN}} = 60 - 20 = 40\) (cm2) Có \({S_{NAM}} = {S_{NCM}} = 40\) (cm2) (\(AM = CM\), chung chiều cao hạ từ N xuống AC). Do đó \({S_{ANC}} = {S_{NAM}} + {S_{NCM}} = 40 + 40 = 80\) (cm2) Mà \({S_{DAM}} - {S_{NAM}} = {S_{DCM}} - {S_{NCM}}\) nên \({S_{DAN}} = {S_{DCN}} = 20\)(cm2) Ta có \(\frac{{{S_{DAN}}}}{{{S_{ANC}}}} = \frac{{20}}{{80}} = \frac{1}{4}\) nên chiều cao hạ từ D xuống AN bằng \(\frac{1}{4}\)chiều cao hạ từ C xuống AN. Có \({S_{DNP}} = \frac{1}{4} \times {S_{CNP}}\) (chung đáy NP và chiều cao hạ từ D xuống AN bằng \(\frac{1}{4}\)chiều cao hạ từ C xuống AN). Mà \({S_{DNP}} + {S_{CNP}} = {S_{DCN}}\) nên \({S_{DNP}} = \frac{1}{5} \times {S_{DCN}} = \frac{1}{5} \times 20 = 4\) (cm2). Đáp số: a) SABCD = 180cm2 b) SDNP = 4 cm2
|