Đề thi vào lớp 6 môn Toán trường Amsterdam năm 2022

Đề bài

ĐỀ THI VÀ ĐÁP ÁN TUYỂN SINH VÀO LỚP 6 TRƯỜNG AMSTERDAM

MÔN: TOÁN

NĂM HỌC 2022 – 2023

Phần I. Điền câu trả lời vào ô trống
Câu 1. Tính: 0,14 × 253 × 3 – 4,2 x 5,3

Câu 2. Biết số \(\overline {2022ab} \) chia hết cho cả 5 và 9 (b > 0). Tìm $a \times b$

Câu 3. Tính $\left( {1 - \frac{1}{2}} \right) \times \left( {1 - \frac{1}{3}} \right) \times \left( {1 - \frac{1}{4}} \right) \times .... \times \left( {1 - \frac{1}{{2022}}} \right)$

Câu 4. Cho ba số có tổng bằng 2022. Biết số thứ nhất bằng $\frac{1}{3}$ số thứ hai, số thứ ba gấp đôi số thứ nhất. Tìm số lớn nhất.

Câu 5. Một ô tô đi từ địa điểm A đến địa điểm B. Cùng lúc đó, 1 ô tô khác đi từ B về A, gặp ô tô thứ nhất tại điểm cách điểm A 140km. Biết ô tô thứ nhất đi từ A đến B hết 8 giờ và ô tô thứ hai đi từ B về A hết 7 giờ. Tính quãng đường AB.

Câu 6. Một bể nước hình hộp chữ nhật có chiều dài 3m, chiều rộng 2m và chiều cao 1,6m. Người ta mở vòi cho nước chảy vào bể thì sau 1 giờ 15 phút bể đầy. Biết trong 1 giờ vòi chảy được 6756 lít nước. Hỏi ban đầu, trong bể có bao nhiêu lít nước?

Câu 7. Cho hai số có tổng là 4055. Biết số bé có hai chữ số tận cùng là 23 và khi đổi chỗ hai chữ số cho nhau ta được số lớn. Tìm tích hai số đó.

Câu 8. Có 18 lít nước được đựng trong các chai loại 400ml, 600ml, 1$\ell $, mỗi loại có ít nhất 1 chai. Hỏi có nhiều nhất bao nhiêu chai loại 600ml.

Câu 9. Có 3 hộp bi A, B, mỗi hộp có 9 viên bi trắng, 9 viên bi xanh và 9 viên bi đỏ. Chuyển từ hộp A sang hộp B 10 viên bi. Hỏi cần chuyển từ hộp B sang hộp A bao nhiêu viên bi để chắc chắn hộp A có ít nhất 8 viên bi mỗi loại.

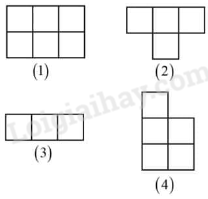
Câu 10. Cho 4 mảnh được tạo thành từ các ô vuông cạnh 1 cm như hình vẽ. Ghép 4 mảnh đó thành 1 hình chữ nhật, tính chu vi hình chữ nhật ghép được.

Câu 11. Cho hình chữ nhật ABCD (AB = 16cm; BC = 12cm), M là trung điểm của BC. Lấy điểm P trên cạnh AB và điểm Q trên cạnh CD sao cho AP = CQ. Tính diện tích tam giác PMQ.

Câu 12. Cho 5 số $a,\,b,\,c,\,d,\,e$ thỏa mãn $\frac{{487}}{{340}} = a + \frac{1}{{b + \frac{1}{{c + \frac{1}{{d + \frac{1}{e}}}}}}}$ . Tính $a + b + c + d + e$

Phần II. Tự luận
Bài 1. Lớp 5A có số học sinh nam gấp đôi số học sinh nữ. Sau khi chuyển đi 2 học sinh nữ thì số học sinh nam bằng $\frac{5}{2}$ số học sinh nữ. Hỏi ban đầu lớp đó có bao nhiêu học sinh?

Bài 2. Minh đi từ A đến B, cùng lúc đó Ngọc đi từ B về A. Hai bạn gặp nhau lần thứ nhất ở điểm cách A 7km. Sau đó, Minh lại đi tiếp tới B, Ngọc lại đi tiếp tới A rồi hai bạn quay trở về. Họ gặp nhau lần thứ hai ở điểm cách B 5km. Hỏi quãng đường AB dài bao nhiêu km?

Bài 3. Cho hình thang ABCD, lấy điểm M trên đường chéo AC sao cho AM = 2 × MC.
Lấy điểm N trên cạnh CD sao cho BDNM là hình thang.
a) So sánh diện tích hai tam giác BDN và BDM.
b) Tính tỉ số $\frac{{{S_{ABND}}}}{{{S_{BNC}}}}$

Đáp án

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1. Tính: 0,14 × 253 × 3− 4,2 × 5,3
Cách giải
0,14 × 253 × 3− 4,2 × 5,3

= 0,42 × 253 − 4, 2 × 5,3

= 4,2 × 25,3 − 4,2 × 5,3
= 4,2 x (25,3 – 5,3)

= 4,2 x 20

= 84

Câu 2. Biết số \(\overline {2022ab} \) chia hết cho cả 5 và 9 (b > 0). Tìm $a \times b$
Cách giải:
Vì số \(\overline {2022ab} \) chia hết cho cả 5 và b > 0 nên b = 5.
Ta có số $\overline {2022a5} $
Vì số $\overline {2022a5} $ chia hết cho 9 nên (2 + 0 + 2 + 2 + a + 5) chia hết cho 9.
Hay (a + 11) chia hết cho 9, suy ra a = 7.
Vậy a x b = 35

Câu 3. Tính $\left( {1 - \frac{1}{2}} \right) \times \left( {1 - \frac{1}{3}} \right) \times \left( {1 - \frac{1}{4}} \right) \times .... \times \left( {1 - \frac{1}{{2022}}} \right)$
Cách giải

$\left( {1 - \frac{1}{2}} \right) \times \left( {1 - \frac{1}{3}} \right) \times \left( {1 - \frac{1}{4}} \right) \times .... \times \left( {1 - \frac{1}{{2022}}} \right) = \frac{1}{2} \times \frac{2}{3} \times \frac{3}{4} \times .... \times \frac{{2021}}{{2022}} = \frac{1}{{2022}}$

Câu 4. Cho ba số có tổng bằng 2022. Biết số thứ nhất bằng $\frac{1}{3}$ số thứ hai, số thứ ba gấp đôi số thứ nhất. Tìm số lớn nhất.
Cách giải
Coi số thứ nhất là 1 phần thì số thứ hai là 3 phần, số thứ ba là 2 phần.
Do đó số lớn nhất là số thứ hai.
Tổng số phần bằng nhau là: 1 + 3 + 2 = 6 (phần)
Số lớn nhất là: 2022 : 6 × 3 = 1011

Câu 5. Một ô tô đi từ địa điểm A đến địa điểm B. Cùng lúc đó, 1 ô tô khác đi từ B về A, gặp ô tô thứ nhất tại điểm cách điểm A 140km. Biết ô tô thứ nhất đi từ A đến B hết 8 giờ và ô tô thứ hai đi từ B về A hết 7 giờ. Tính quãng đường AB.
Cách giải

Tỉ số thời gian đi hết quãng đường AB của ô tô thứ nhất so với ô tô thứ hai là: $8:7 = \frac{8}{7}$
Xét trên cùng quãng đường AB, thời gian và vận tốc tỉ lệ nghịch với nhau nên tỉ số vận tốc của ô tô thứ nhất so với ô tô thứ hai là $\frac{7}{8}$
Khi hai ô tô gặp nhau thì thời gian đi của hai ô tô bằng nhau (do hai xe xuất phát cùng lúc).
Vì cùng thời gian, quãng đường đi được và vận tốc của xe tỉ lệ thuận nên tỉ số quãng đường của ô tô thứ nhất so với ô tô thứ hai là $\frac{7}{8}$.
Do hai xe gặp nhau tại điểm cách A 140km nên ô tô thứ nhất đi được 140km.
Quãng đường ô tô thứ hai đi được khi gặp nhau là: $140:\frac{7}{8} = 160$ (km).
Độ dài quãng đường AB là: 140 + 160 = 300 (km).

                                  Đáp số: 300 km

Câu 6. Một bể nước hình hộp chữ nhật có chiều dài 3m, chiều rộng 2m và chiều cao 1,6m. Người ta mở vòi cho nước chảy vào bể thì sau 1 giờ 15 phút bể đầy. Biết trong 1 giờ vòi chảy được 6756 lít nước. Hỏi ban đầu, trong bể có bao nhiêu lít nước?

Cách giải:
Thể tích của bể là 3 × 2 × 1,6 = 9,6 (m³)
Đối 9,6m³ = 9600dm³ = 9600 lít; 1 giờ 15 phút = $\frac{5}{4}$ giờ
Trong 1 giờ 15 phút, vòi chảy được số lít nước là: $6756 \times \frac{5}{4} = 8445$ (lít nước)
Ban đầu, trong bể có số lít nước là: 9600 – 8445 = 1155 (lít nước)

                        Đáp số: 1155 lít nước

Câu 7. Cho hai số có tổng là 4055. Biết số bé có hai chữ số tận cùng là 23 và khi đổi chỗ hai chữ số cho nhau ta được số lớn. Tìm tích hai số đó.

Cách giải

Gọi số bé là $\overline {X23} $ thì số lớn là $\overline {X32} $
Vì tổng 2 số là 4055 nên $\overline {X23} $ +$\overline {X32} $ = 4055

$ \Rightarrow $ X × 100 + 23 + X × 100 + 32 = 4055
$ \Rightarrow $X × 200 + 55 = 4055

$ \Rightarrow $ X x 200 = 4000 $ \Rightarrow $ X = 200
Vậy số bé là 2023, số lớn là 2032

Tích hai số là: 2023 × 2032 = 4110736

Câu 8. Có 18 lít nước được đựng trong các chai loại 400ml, 600ml, 1$\ell $, mỗi loại có ít nhất 1 chai. Hỏi có nhiều nhất bao nhiêu chai loại 600ml.
Cách giải

Để số chai loại 600 ml là nhiều nhất thì số chai loại 400ml và 1$\ell $ phải ít nhất.
Vì tổng số lít nước trong tất cả các chai là 18 lít là số chia hết cho 3, tổng số lít nước có trong chai loại 600ml cũng là số chia hết cho 3 nên tổng số lít nước có trong các chai loại 400ml và 1$\ell $ phải chia hết cho 3. (1)
Theo bài ra, mỗi loại có ít nhất 1 chai nên tổng số lít nước trong chai 400ml và 1$\ell $ phải lớn hơn hoặc bằng 1400ml. (2)
Kết hợp (1) và (2), suy ra tổng số nước trong chai loại 400ml và 11 ít nhất là 1800ml.
Vậy số chai loại 600ml nhiều nhất là: (18000 – 1800) = 27 (chai)

Câu 9. Có 3 hộp bi A, B, mỗi hộp có 9 viên bi trắng, 9 viên bi xanh và 9 viên bị đỏ. Chuyển từ hộp A sang hộp B 10 viên bi. Hỏi cần chuyển từ hộp B sang hộp A bao nhiêu viên bi để chắc chắn hộp A có ít nhất 8 viên bi mỗi loại.
Cách giải:
Mỗi hộp có số viên bi là 9 + 9 + 9 = 27 (viên bi)
Số bi của hộp A sau khi chuyển từ hộp A sang hộp B 10 viên bi là 27 – 10 = 17 (viên bi)
Khả năng xấu nhất mà hộp A không có 8 viên bi mỗi loại là trong hộp A có 43 viên bi trong đó có hai loại màu bi có 18 viên và màu bi còn lại có 7 viên.
Do đó, để chắc chắn hộp A có ít nhất 8 viên bi mỗi loại thì trong hộp A phải có 44 viên bi.
Vậy cần chuyển số viên bi từ hộp B sang hộp A là: 44 – 17 = 27 (viên).

Câu 10. Cho 4 mảnh được tạo thành từ các ô vuông cạnh 1 cm như hình vẽ. Ghép 4 mảnh đó thành 1 hình chữ nhật, tính chu vi hình chữ nhật ghép được.

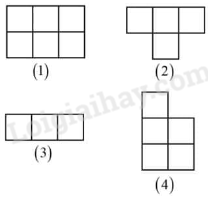
Cách giải
Tổng diện tích của cả 4 mảnh là: 18 × 1 × 1 = 18 (cm²)
Vì 18 = 1 x 18 = 2 x 9 = 3 x 6 nên hình chữ nhật ghép được có kích thước thuộc một trong các trường hợp sau: 1 x 18; 2 × 9; 3 × 6.
Do mảnh (1) có kích thước 2 × 3 nên ta loại trường hợp ghép được thành hình chữ nhật có kích thước 1 × 18.
Với trường hợp kích thước 2 × 9, ta chỉ có thể ghép các hình theo hàng ngang gắn với chiều rộng của hình (1) (không ghép được, do đó loại).
Vậy ta chỉ có thể ghép theo kích thước 3 × 6.
Chu vi hình chữ nhật ghép được là: 2 x (3 + 6) = 18(cm).
Hình minh họa:

Câu 11. Cho hình chữ nhật ABCD (AB = 16cm; BC = 12cm), M là trung điểm của BC. Lấy điểm P trên cạnh AB và điểm Q trên cạnh CD sao cho AP = CQ. Tính diện tích tam giác PMQ.

Cách giải:

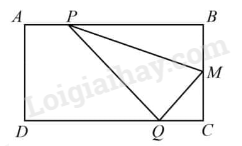
Vì AP = CQ và AB = CD nên BP = DQ

Do đó hai hình thang APQD và BCQP có diện tích bằng nhau.

$ \Rightarrow {S_{APQD}} = {S_{BCQP}} = \frac{1}{2} \times {S_{ABCD}}$

Ta có ${S_{BPM}} = \frac{1}{2} \times BM \times PB$

${S_{CMQ}} = \frac{1}{2} \times CM \times QC$

Vì M là trung điểm của BC nên $BM = CM = \frac{1}{2} \times BC$

$ \Rightarrow {S_{BPM}} + {S_{CMQ}} = \frac{1}{2} \times \frac{1}{2} \times BC \times PB + \frac{1}{2} \times \frac{1}{2} \times BC \times QC$

$ = \frac{1}{4} \times BC \times (PB + QC) = \frac{1}{4} \times BC \times AB = \frac{1}{4} \times {S_{ABCD}}$

Vậy ${S_{PMQ}} = {S_{BCQP}} - (S{}_{BPM} + {S_{CMQ}}) = \frac{1}{2} \times {S_{ABCD}} - \frac{1}{4} \times {S_{ABCD}} = \frac{1}{4} \times {S_{ABCD}} = \frac{1}{4} \times 12 \times 16 = 48$ (cm²)

Câu 12. Cho 5 số $a,\,b,\,c,\,d,\,e$ thỏa mãn $\frac{{487}}{{340}} = a + \frac{1}{{b + \frac{1}{{c + \frac{1}{{d + \frac{1}{e}}}}}}}$ . Tính $a + b + c + d + e$

Cách giải:

Ta có $\frac{{487}}{{340}} = 1 + \frac{{147}}{{340}} = 1 + \frac{1}{{\frac{{340}}{{147}}}} = 1 + \frac{1}{{2 + \frac{{46}}{{147}}}} = 1 + \frac{1}{{2 + \frac{1}{{\frac{{147}}{{46}}}}}} = 1 + \frac{1}{{2 + \frac{1}{{3 + \frac{9}{{46}}}}}} = 1 + \frac{1}{{2 + \frac{1}{{3 + \frac{1}{{5 + \frac{1}{9}}}}}}}$

Suy ra a = 1, b = 2, c = 3, d = 5, e = 9

Vậy a + b + c + d + e = 20

PHẦN 2. TỰ LUẬN

Bài 1. Lớp 5A có số học sinh nam gấp đôi số học sinh nữ. Sau khi chuyển đi 2 học sinh nữ thì số học sinh nam bằng $\frac{5}{2}$ số học sinh nữ. Hỏi ban đầu lớp đó có bao nhiêu học sinh?

Cách giải:
Ban đầu, số học sinh nam gấp đôi số học sinh nữ nên số học sinh nữ bằng $\frac{1}{2}$ số học sinh nam.
Lúc sau, số học sinh nam bằng $\frac{5}{2}$ số học sinh nữ nên số học sinh nữ bằng $\frac{2}{5}$số học sinh nam.
2 học sinh ứng với: $\frac{1}{2} - \frac{2}{5} = \frac{1}{{10}}$ (số học sinh nam)
Số học sinh nam là: $2:\frac{1}{{10}} = 20$ (bạn)
Số học sinh nữ lúc đầu là: 20 : 2 = 10 (học sinh)
Ban đầu, lớp đó có số học sinh là: 20 + 10 = 30 (học sinh)
                  Đáp số: 30 học sinh.

Bài 2. Minh đi từ A đến B, cùng lúc đó Ngọc đi từ B về A. Hai bạn gặp nhau lần thứ nhất ở điểm cách A 7km. Sau đó, Minh lại đi tiếp tới B, Ngọc lại đi tiếp tới A rồi hai bạn quay trở về. Họ gặp nhau lần thứ hai ở điểm cách B 5km. Hỏi quãng đường AB dài bao nhiêu km?
Cách giải:

Gọi C là điểm hai bạn gặp nhau lần thứ nhất và D là điểm hai bạn gặp nhau lần thứ hai.
Ta có AC = 7km và BD = 5km. Khi hai bạn gặp nhau lần đầu thì tổng quãng đường hai bạn đi được bằng quãng đường AB. Khi hai bạn gặp nhau lần thứ hai thì tổng quãng đường hai bạn đi được gấp 3 lần quãng đường AB.

Do vận tốc hai bạn không đổi nên để hai bạn đi được quãng đường gấp 3 lần quãng đường AB thì cần thời gian gấp 3 lần để đi hết quãng đường AB.
Suy ra, quãng đường bạn Minh đi được đến khi gặp nhau lần thứ hai gấp 3 lần quãng đường bạn Minh đi được khi gặp nhau lần thứ nhất.
Quãng đường bạn Minh đi được đến khi gặp nhau lần thứ hai là: 7 × 3 = 21 (km).
Độ dài quãng đường AB là: 21 – 5 = 16 (km)
          Đáp số: 16km

Bài 3. Cho hình thang ABCD, lấy điểm M trên đường chéo AC sao cho AM = 2 × MC.
Lấy điểm N trên cạnh CD sao cho BDNM là hình thang.
a) So sánh diện tích hai tam giác BDN và BDM.
b) Tính tỉ số $\frac{{{S_{ABND}}}}{{{S_{BNC}}}}$

Cách giải:

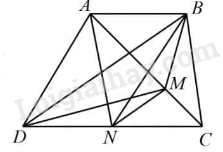
a) Vì BDNM là hình thang nên S_BDN = S_BMD (hai tam giác có chung đáy BD, chiều cao hạ từ N xuống BD bằng chiều cao hạ từ M xuống BD cùng bằng chiều cao hình thang BDNM ).
b) Vì AM = 2 × MC nên S_ABM = 2 x S_BMC (hai tam giác có chung chiều cao hạ từ B xuống AC).
Vì AM = 2 × MC nên S_ANM = 2 x S_MNC (hai tam giác có chung chiều cao hạ từ N xuống AC).

Suy ra S_ABMN = S_ABM + S_ANM = 2 x S_BMC + 2 x S_MNC = 2 x (S_BMC + S_MNC)

Mà S_ABMN = S_NAB + S_NMB và S_NAB = S_DAB nên S_DAB + S_NMB = 2 x (S_BMC + S_MBC)

$ \Rightarrow $S_DAB = 3 x S_NMB = 2 x (S_BMC +S_MNC + S_NMB) = 2 x S_BNC (1)

Lại có S_ADC = 3 x S_MDC (hai tam giác có chung chiều cao hạ từ D xuống AC và AM = 2 x MC)

Mà hai tam giác này có chung đáy CD nên chiều cao hạ từ A xuống CD gấp 3 lần chiều cao hạ từ M xuống CD.
Mặt khác, chiều cao hạ từ A xuống CD bằng chiều cao hạ từ B xuống CD

$ \Rightarrow $ Chiều cao hạ từ B xuống CD gấp 3 lần chiều cao hạ từ M xuống CD.

Do đó S_BDN = 3 x S_MDN

Vì BDNM là hình thang nên S_MDN = S_NMB $ \Rightarrow $S_BDN = 3 x S_NMB

Thay vào (1) ta được S_DAB + S_BDN = 2 x S_BNC

$ \Rightarrow $ S_ABND = 2 x S_BNC  $ \Rightarrow $ $\frac{{{S_{ABND}}}}{{{S_{BNC}}}} = 2$