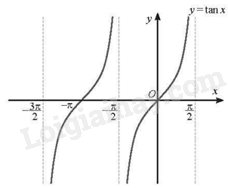
Giải bài 5 trang 27 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Đề bài

Cho hàm số \(y = \tan x\) với \(x \in \left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) \cup \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).

a) Vẽ đồ thị của hàm số đã cho.

b) Tìm các giá trị của \(x \in \left[ { - \frac{{7\pi }}{4};\frac{\pi }{4}} \right]\) sao cho \(\sqrt 3 \tan \left( {x + \frac{\pi }{4}} \right) + 1 = 0\).

c) Tìm các giá trị của \(x \in \left[ { - \frac{{5\pi }}{6};\frac{\pi }{6}} \right]\) sao cho \(\tan \left( {2x + \frac{\pi }{6}} \right) \ge  - \frac{{\sqrt 3 }}{3}\).

Lời giải chi tiết

a) Ta có đồ thị của hàm số \(y = \tan x\) với \(x \in \left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) \cup \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\):

b) \(\sqrt 3 \tan \left( {x + \frac{\pi }{4}} \right) + 1 = 0\) khi \(\tan \left( {x + \frac{\pi }{4}} \right) = \frac{{ - \sqrt 3 }}{3}\)

Đặt \(x + \frac{\pi }{4} = t\). Vì \(\frac{{ - 7\pi }}{4} \le x \le \frac{\pi }{4} \Rightarrow \frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\)

Hàm số \(y = \tan t\) xác định khi \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\). Kết hợp với điều kiện \(\frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\) ta có \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\).

Đồ thị hàm số \(y = \tan t\) với \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\) là:

Từ đồ thị hàm số trên ta có:

\(\tan t = \frac{{ - \sqrt 3 }}{3}\) khi và chỉ khi \(t = \frac{{ - 7\pi }}{6}\) hoặc \(t = \frac{{ - \pi }}{6}\).

Suy ra: \(x + \frac{\pi }{4} = \frac{{ - 7\pi }}{6}\) hoặc \(x + \frac{\pi }{4} = \frac{{ - \pi }}{6}\). Do đó, \(x = \frac{{ - 17\pi }}{{12}}\) hoặc \(x = \frac{{ - 5\pi }}{{12}}\).

c) Đặt \(2x + \frac{\pi }{6} = t\). Vì \(\frac{{ - 5\pi }}{6} \le x \le \frac{\pi }{6} \Rightarrow \frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\)

Hàm số \(y = \tan t\) xác định khi \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\). Kết hợp với điều kiện \(\frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\) ta có \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\)

Đồ thị hàm số \(y = \tan t\) với \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\) là:

Từ đồ thị hàm số trên ta có:

\(\tan t \ge \frac{{ - \sqrt 3 }}{3}\) khi và chỉ khi \(\frac{{ - 7\pi }}{6} \le t <  - \frac{\pi }{2}\) hoặc \(\frac{{ - \pi }}{6} \le t < \frac{\pi }{2}\).

Suy ra, \(\frac{{ - 7\pi }}{6} \le 2x + \frac{\pi }{6} <  - \frac{\pi }{2}\) hoặc \(\frac{{ - \pi }}{6} \le 2x + \frac{\pi }{6} < \frac{\pi }{2}\)

Do đó, \(\frac{{ - 2\pi }}{3} \le x <  - \frac{\pi }{3}\) hoặc \( - \frac{\pi }{6} \le x < \frac{\pi }{6}\).