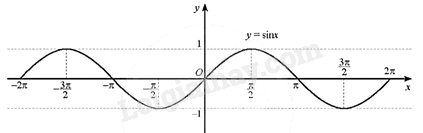
Giải bài 4 trang 27 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Đề bài

Cho hàm số $y = \sin x$ với $x \in \left[ { - 2\pi ;2\pi } \right]$.

a) Vẽ đồ thị hàm số đã cho.

b) Tìm các giá trị của $x \in \left[ {\frac{{ - 5\pi }}{3};\frac{{7\pi }}{3}} \right]$ sao cho $\sin \left( {\frac{\pi }{3} - x} \right) =  - 1$.

c) Tìm các giá trị của $x \in \left[ {\frac{{ - 9\pi }}{8};\frac{{7\pi }}{8}} \right]$ sao cho $\sin \left( {2x + \frac{\pi }{4}} \right) > 0$.

d) Tìm m để có bốn giá trị $\alpha  \in \left[ { - 2\pi ;2\pi } \right]$ phân biệt thỏa mãn $\sin \alpha  = m$.

Lời giải chi tiết

a) Ta có đồ thị hàm số $y = \sin x$ với $x \in \left[ { - 2\pi ;2\pi } \right]$:

b) Đặt $\frac{\pi }{3} - x = t$. Vì $\frac{{ - 5\pi }}{3} \le x \le \frac{{7\pi }}{3} \Rightarrow  - 2\pi  \le t \le 2\pi$.

Từ đồ thị hàm số trong phần a, ta có: $\sin t =  - 1$ khi và chỉ khi $t = \frac{{ - \pi }}{2}$ hoặc $t = \frac{{3\pi }}{2}$

Do đó, $\frac{\pi }{3} - x = \frac{{ - \pi }}{2}$ hoặc $\frac{\pi }{3} - x = \frac{{3\pi }}{2}$. Suy ra: $x = \frac{{5\pi }}{6}$ hoặc $x = \frac{{ - 7\pi }}{6}$

c) Đặt $2x + \frac{\pi }{4} = t$. Vì $\frac{{ - 9\pi }}{8} \le x \le \frac{{7\pi }}{8} \Rightarrow  - 2\pi  \le t \le 2\pi$.

Từ đồ thị hàm số trong phần a, ta có: $\sin t > 0$ khi và chỉ khi $- 2\pi  < t <  - \pi$ hoặc $0 < t < \pi$

Suy ra: $- 2\pi  < 2x + \frac{\pi }{4} <  - \pi$ hoặc $0 < 2x + \frac{\pi }{4} < \pi$

Do đó, $\frac{{ - 9\pi }}{8} \le x \le \frac{{ - 5\pi }}{8}$ hoặc $\frac{{ - \pi }}{8} \le x \le \frac{{3\pi }}{8}$

d) Có bốn giá trị $\alpha  \in \left[ { - 2\pi ;2\pi } \right]$ phân biệt thỏa mãn $\sin \alpha  = m$ khi và chỉ khi đường thẳng $y = m$ cắt đồ thị hàm số $y = \sin \alpha$ tại bốn điểm. Từ đồ thị hàm số ở trên, điều này xảy ra khi và chỉ khi $- 1 < m < 0$ hoặc $0 < m < 1$.