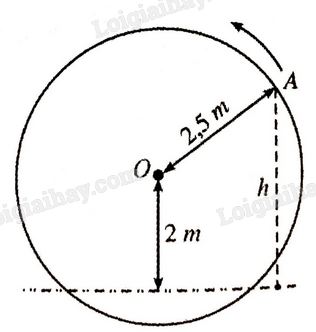
SBT Toán 11 - giải SBT Toán 11 - Kết nối tri thức với cuộc sống

Giải bài 1.29 trang 24 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Một chiếc guồng nước có dạng hình tròn bán kính 2,5m; trục của nó đặt cách mặt nước 2m (hình bên).

Đề bài

Một chiếc guồng nước có dạng hình tròn bán kính 2,5m; trục của nó đặt cách mặt nước 2m (hình bên). Khi guồng quay đều, khoảng cách h (mét) tính từ một chiếc gầu gắn tại điểm A trên guồng đến mặt nước là \(h = \left| y \right|\) trong đó \(y = 2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right)\) với x là thời gian quay của guồng \(\left( {x \ge 0} \right),\) tính bằng phút; ta quy ước rằng \(y > 0\) khi gầu ở trên mặt nước và \(y < 0\) khi gầu ở dưới mặt nước.

a) Khi nào chiếc gầu ở vị trí cao nhất? Thấp nhất?

b) Chiếc gầu cách mặt nước 2 mét lần đầu tiên khi nào?

Phương pháp giải - Xem chi tiết

* Sử dụng kiến thức \( - 1 \le \sin x \le 1\) với mọi x

* Sử dụng cách giải phương trình \(\sin x = m\) (1)

+ Nếu \(\left| m \right| > 1\) thì phương trình (1) vô nghiệm.

+ Nếu \(\left| m \right| \le 1\) thì tồn tại duy nhất số \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) thỏa mãn \(\sin \alpha = m\).

Khi đó, phương trình (1) tương đương với:

\(\sin x = m \Leftrightarrow \sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)

Lời giải chi tiết

a) Vì \( - 1 \le \sin 2\pi \left( {x - \frac{1}{4}} \right) \le 1\) nên \( - 2,5 \le 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) \le 2,5\)

Do đó, \( - 0,5 = 2 - 2,5 \le 2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) \le 2 + 2,5 = 4,5\;\forall x \in \mathbb{R}\)

Suy ra, gầu ở vị trí cao nhất khi \(\sin 2\pi \left( {x - \frac{1}{4}} \right) = 1 \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = \frac{\pi }{2} + k2\pi \Leftrightarrow x = \frac{1}{2} + k\left( {k \in \mathbb{Z}} \right)\)

Vì gầu ở vị trí cao nhất tại các thời điểm \(\frac{1}{2},\frac{3}{2},\frac{5}{2},...\) phút

Tương tự, gầu ở vị trí thấp nhất khi \(\sin 2\pi \left( {x - \frac{1}{4}} \right) = - 1 \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = - \frac{\pi }{2} + k2\pi \Leftrightarrow x = k\left( {k \in \mathbb{Z}} \right)\)

Vì gầu ở vị trí cao nhất tại các thời điểm 0, 1, 2, 3… phút

b) Gầu cách mặt nước 2m khi \(2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) = 2 \Leftrightarrow 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) = 0 \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = k\pi \Leftrightarrow x = \frac{1}{4} + \frac{k}{2}\left( {k \in \mathbb{Z}} \right)\)

Vậy chiếc gầu cách mặt nước 2m lần đầu tại thời điểm \(x = \frac{1}{4}\) phút