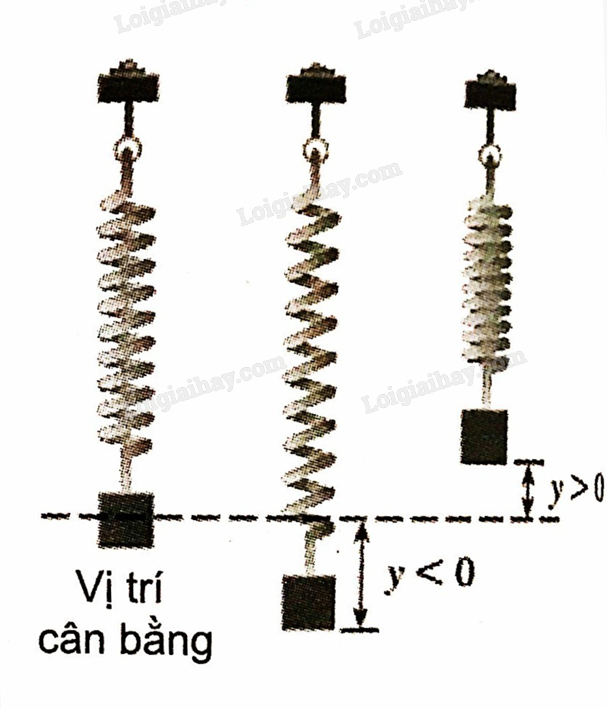
Giải bài 1.23 trang 18 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Đề bài

Một con lắc lò xo dạo động điều hòa quanh vị trí cân bằng theo phương trình

ở đó \(y = 25\sin 4\pi t\), y được tính bằng centimet còn thời gian t được tính bằng giây.

a) Tìm chu kì dao động của con lắc lò xo.

b) Tìm tần số dao động của con lắc, tức là số lần dao động trong một giây.

c) Tìm khoảng cách giữa điểm cao nhất và điểm thấp nhất của con lắc.

Lời giải chi tiết

a) Hàm số \(y = 25\sin 4\pi t\) tuần hoàn với chu kì \(T = \frac{{2\pi }}{{4\pi }} = \frac{1}{2}\). Suy ra chu kì dao động của con lắc lò xo (tức là khoảng thời gian để con lắc thực hiện được một dao động toàn phần) là \(T = \frac{1}{2}\) (giây).

b) Vì chu kì dao động của con lắc là \(T = \frac{1}{2}\) (giây) nên trong 1 giây con lắc thực hiện được 2 dao động, tức là tần số dao động của con lắc là \(f = \frac{1}{T} = 2\,{\rm{Hz}}\).

c) Vì phương trình dao động của con lắc là \(y = 25\sin 4\pi t\), nên biên độ dao động của nó là A=25cm. Từ đó, khoảng cách giữa điểm cao nhất và điểm thấp nhất của con lắc là 2A=50cm.