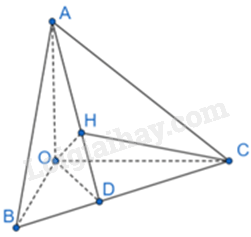
Giải bài 1 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Đề bài

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Chứng minh rằng:

a) $BC \bot \left( {OAH} \right)$.

b) H là trực tâm của $\Delta ABC$.

c) $\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}$.

Quảng cáo

Lời giải chi tiết

a) Vì H là hình chiếu của O trên mặt phẳng (ABC) nên $OH \bot \left( {ABC} \right) \Rightarrow OH \bot BC$

Vì $OA \bot OB,OA \bot OC \Rightarrow OA \bot \left( {BOC} \right) \Rightarrow OA \bot BC$

Ta có: $OA \bot BC,OH \bot BC \Rightarrow BC \bot \left( {OAH} \right)$

b) Vì $BC \bot \left( {OAH} \right)$  nên $BC \bot AH$ (1)

Vì $OH \bot \left( {ABC} \right) \Rightarrow OH \bot AC$

Vì $OA \bot OB,OB \bot OC \Rightarrow OB \bot \left( {AOC} \right) \Rightarrow OB \bot AC$

Ta có: $OB \bot AC,OH \bot AC \Rightarrow AC \bot \left( {OBH} \right) \Rightarrow AC \bot BH$ (2)

Mà H là giao điểm của BH và CH (3)

Từ (1), (2) và (3) ta có: H là trực tâm của $\Delta ABC$.

c) Gọi D là giao điểm của AH và BC. Khi đó, $OD \bot BC$

Vì $OA \bot \left( {BOC} \right) \Rightarrow OA \bot OD$

Do đó, tam giác AOD vuông tại O. Mà OH là đường cao nên $\frac{1}{{O{H^2}}} = \frac{1}{{O{D^2}}} + \frac{1}{{O{A^2}}}$

Tam giác BOC vuông tại O, đường cao OD có: $\frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}$

Vậy $\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}$