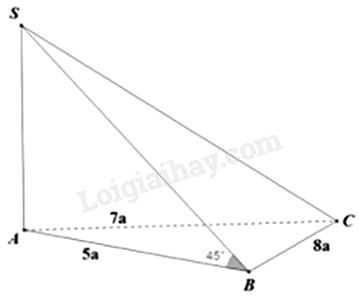
Giải bài 4 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2Cho khối chóp S.ABC có \(SA \bot \left( {ABC} \right)\), tam giác ABC có độ dài 3 cạnh là \(AB = 5a,BC = 8a,AC = 7a\), góc giữa SB và (ABC) là \({45^0}\). Tính thể tích khối chóp S.ABC. Đề bài Cho khối chóp S.ABC có \(SA \bot \left( {ABC} \right)\), tam giác ABC có độ dài 3 cạnh là \(AB = 5a,BC = 8a,AC = 7a\), góc giữa SB và (ABC) là \({45^0}\). Tính thể tích khối chóp S.ABC. Phương pháp giải - Xem chi tiết - Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính: + Nếu đường thẳng a vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a với (P) bằng \({90^0}\). + Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a và hình chiếu a’ của a trên (P) gọi là góc giữa đường thẳng a và (P). - Sử dụng kiến thức về thể tích hình chóp: Thể tích hình chóp bằng một phần ba diện tích đáy nhân với chiều cao: \(V = \frac{1}{3}S.h\) Lời giải chi tiết
Vì \(SA \bot \left( {ABC} \right)\) nên A là hình chiếu của S trên mặt phẳng (ABC) Ta có: \(\left( {SB,\left( {ABC} \right)} \right) = \left( {SB,AB} \right) = \widehat {SBA} = {45^0}\) Vì \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AB\). Do đó, tam giác SAB vuông cân tại A. Suy ra, \(SA = AB = 5a\). Nửa chu vi tam giác ABC là: \(p = \frac{{5a + 7a + 8a}}{2} = 10a\) Diện tích tam giác ABC là: \({S_{ABC}} = \sqrt {10a\left( {10a - 5a} \right)\left( {10a - 7a} \right)\left( {10a - 8a} \right)} = 10{a^2}\sqrt 3 \) Thể tích khối chóp S. ABC là: \(V = \frac{1}{3}SA.{S_{ABC}} = \frac{1}{3}.5a.10{a^2}\sqrt 3 = \frac{{50{a^3}\sqrt 3 }}{3}\)  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
