Bài tập trắc nghiệm Toán 8 - Chân trời sáng tạo

Trắc nghiệm Bài 1: Hai tam giác đồng dạng Toán 8 Chân trời sáng tạo

Làm đề thi

Đề bài

Câu 1 :

Hãy chọn câu đúng.

  • A
    Hai tam giác bằng nhau thì đồng dạng.
  • B
    Hai tam giác đồng dạng thì bằng nhau.
  • C
    Hai tam giác bằng nhau thì không đồng dạng.
  • D
    Hai tam giác vuông luôn đồng dạng với nhau.
Câu 2 :

Hãy chọn câu sai.

  • A
    Hai tam giác bằng nhau thì đồng dạng.
  • B
    Hai tam giác đều luôn đồng dạng.
  • C
    Hai tam giác cân thì đồng dạng.
  • D
    Hai tam giác đồng dạng là hai tam giác có tất cả các cặp góc tương ứng bằng nhau và các cặp cạnh tương ứng tỉ lệ.
Câu 3 :

Cho \(\Delta ABC,\Delta MNP\) nếu có \(\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P\) để \(\Delta ABC \backsim \Delta MNP\) theo định nghĩa hai tam giác đồng dạng thì cần bổ sung thêm điều kiện nào?

  • A
    \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) .
  • B
    \(\frac{{AB}}{{NP}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NM}}\) .
  • C
    \(\frac{{AB}}{{MN}} = \frac{{AC}}{{NP}} = \frac{{BC}}{{MP}}\) .
  • D
    \(\frac{{AB}}{{MP}} = \frac{{AC}}{{NP}} = \frac{{BC}}{{NM}}\) .
Câu 4 :

Cho \(\Delta ABC \backsim \Delta MNP\) theo tỉ số 2. Khẳng định nào sau đây là đúng

  • A
    \(MN = 2{\rm{A}}B\) .
  • B
    \(AC = 2NP\) .
  • C
    \(MP = 2BC\) .
  • D
    \(BC = 2.NP\) .
Câu 5 :

Hãy chọn câu đúng

Nếu \(\Delta ABC \backsim \Delta MNP\) theo tỉ số \(k = \frac{2}{3}\) thì \(\Delta MNP \backsim \Delta ABC\) theo tỉ số

  • A
    \(\frac{2}{3}\) .
  • B
    \(\frac{3}{2}\) .
  • C
    \(\frac{4}{9}\) .
  • D
    \(\frac{4}{3}\) .
Câu 6 :

Cho \(\Delta ABC,\Delta MNP\) biết \(AB = 3cm;AC = 4cm;BC = 5cm;MN = 6cm;MP = 8cm;NP = 10cm\) và \(\widehat A = {90^o};\widehat B = {60^o};\widehat M = {90^o};\widehat P = {30^o}\) thì:

  • A
    \(\Delta ABC \backsim \Delta PNM\) .
  • B
    \(\Delta ABC \backsim \Delta NMP\) .
  • C
    \(\Delta ABC \backsim \Delta MNP\) .
  • D
    \(\Delta ABC \backsim \Delta MPN\) .
Câu 7 :

Cho \(\Delta ABC \backsim \Delta D{\rm{EF}}\) biết \(\widehat A = {50^o};\widehat B = {60^o}\) . Khi đó số đo góc D bằng

  • A
    \({50^o}\) .
  • B
    \({60^o}\) .
  • C
    \({70^o}\) .
  • D
    \({80^o}\) .
Câu 8 :

Cho tam giác ABC, trên AB lấy điểm D. Qua D kẻ đường thẳng song song với BC cắt AC ở E. Khẳng định nào sau đâyđúng

  • A
    \(\Delta ABC \backsim \Delta A{\rm{D}}E\) .
  • B
    \(\Delta ABC \backsim \Delta A{\rm{ED}}\) .
  • C
    \(\Delta BAC \backsim \Delta A{\rm{D}}E\) .
  • D
    \(\Delta ACB \backsim \Delta DE{\rm{A}}\) .
Câu 9 :

Cho \(\Delta ABC \backsim \Delta DEF\) theo tỉ số \({k_1}\) , \(\Delta MNP \backsim \Delta D{\rm{EF}}\) theo tỉ số \({k_2}\) . Hỏi \(\Delta ABC \backsim \Delta MNP\) theo tỉ số nào ?

  • A
    \({k_1}\) .
  • B
    \(\frac{{{k_2}}}{{{k_1}}}\) .
  • C
    \(\frac{{{k_1}}}{{{k_2}}}\) .
  • D
    \({k_1}{k_2}\) .
Câu 10 :

Cho \(\Delta ABC \backsim \Delta MNP\) . Biết \(AB = 5cm;BC = 6cm;MN = 10cm;MP = 5cm\) . Hãy chọn đáp án đúng:

  • A
    \(NP = 2,5cm;AC = 12cm\)
  • B
    \(NP = 12cm;AC = 2,5cm\)
  • C
    \(NP = 5cm;AC = 10cm\)
  • D
    \(NP = 10cm;AC = 5cm\)
Câu 11 :

Cho hình vẽ, biết AB // DE. Tính tỉ số độ dài của x và y.

  • A
    18.
  • B
    \(\frac{1}{9}\) .
  • C
    2.
  • D
    \(\frac{1}{2}\) .
Câu 12 :

Cho \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) theo tỉ số \(2:3\) và \(\Delta {A_1}{B_1}{C_1} \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số 1 :3. Vậy \(\Delta ABC \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số k bằng

  • A
    \(k = 3:9\)
  • B
    \(k = 2:9\)
  • C
    \(k = 2:6\)
  • D
    \(k = 1:3\)
Câu 13 :

Cho \(\Delta {A_1}{B_1}{C_1} \backsim \Delta ABC\) theo tỉ số đồng dạng \(k = \frac{2}{3}\) . Tỉ số chu vi của hai tam giác đó là:

  • A
    \(\frac{4}{9}\).
  • B
    \(\frac{3}{2}\).
  • C
    \(\frac{3}{4}\).
  • D
    \(\frac{2}{3}\).
Câu 14 :

Cho \(\Delta MNI \backsim \Delta ABC\) theo tỉ số \(k = \frac{5}{7}\) và hiệu chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác.

  • A
    \({C_{\Delta MNI}} = 30m,{C_{\Delta ABC}} = 46m.\)
  • B
    \({C_{\Delta MNI}} = 56m,{C_{\Delta ABC}} = 40m.\)
  • C
    \({C_{\Delta MNI}} = 24m,{C_{\Delta ABC}} = 40m.\)
  • D
    \({C_{\Delta MNI}} = 40m,{C_{\Delta ABC}} = 56m.\)
Câu 15 :

Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm E sao cho AC = 3.AE. Qua E vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:

\((I)\Delta AME \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_1} = \frac{1}{3}\)

\((II)\Delta CBA \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_2} = 1\)

\((III)\Delta CNE \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_3} = \frac{2}{3}\)

Chọn câu đúng:

  • A
    (I) đúng, (II) và (III) sai.
  • B
    (I) và (II) đúng, (III) sai.
  • C
    (I) , (II), (III) đều đúng.
  • D
    (I), (II), (III) đều sai.
Câu 16 :

Cho tam giác ABC , lấy M trên cạnh BC sao cho \(\frac{{MB}}{{MC}} = \frac{1}{2}\) Qua M kẻ đường thẳng song song với AC cắt AB tại D và đường thẳng song song với AB cắt AD tại E biết chu vi tam giác MEC bằng 24 cm thì chu vi tam giác DBM là

  • A
    12cm .
  • B
    24 cm.
  • C
    48 cm.
  • D
    36cm .

Lời giải và đáp án

Câu 1 :

Hãy chọn câu đúng.

  • A
    Hai tam giác bằng nhau thì đồng dạng.
  • B
    Hai tam giác đồng dạng thì bằng nhau.
  • C
    Hai tam giác bằng nhau thì không đồng dạng.
  • D
    Hai tam giác vuông luôn đồng dạng với nhau.

Đáp án : A

Phương pháp giải :
Dựa vào định nghĩa hai tam giác đồng dạng.
Lời giải chi tiết :

+ Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1 nên câu A đúng, câu C sai.

+ Hai tam giác đồng dạng thì chưa chắc bằng nhau nó chỉ bằng nhau khi tỉ số đồng dạng bằng 1 nên câu B sai.

+ Hai tam giác vuông chưa chắc đồng dạng (chưa đủ điều kiện các cạnh tương ứng tỉ lệ, các góc tương ứng bằng nhau) nên câu D sai.

Câu 2 :

Hãy chọn câu sai.

  • A
    Hai tam giác bằng nhau thì đồng dạng.
  • B
    Hai tam giác đều luôn đồng dạng.
  • C
    Hai tam giác cân thì đồng dạng.
  • D
    Hai tam giác đồng dạng là hai tam giác có tất cả các cặp góc tương ứng bằng nhau và các cặp cạnh tương ứng tỉ lệ.

Đáp án : C

Phương pháp giải :
Dựa vào định nghĩa hai tam giác đồng dạng.
Lời giải chi tiết :

+ Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1 nên A đúng.

+ Hai tam giác đều có các góc đều bằng \({60^0}\) và các cạnh của mỗi tam giác bằng nhau nên các cạnh tương ứng tỉ lệ . Vậy hai tam giác đều luôn đồng dạng nên B đúng.

+ Hai tam giác cân chưa đủ điều kiện các cạnh tương ứng tỉ lệ, các góc tương ứng bằng nhau nên không đồng dạng nên C sai

+ Câu D đúng vì là định nghĩa hai tam giác đồng dạng.

Câu 3 :

Cho \(\Delta ABC,\Delta MNP\) nếu có \(\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P\) để \(\Delta ABC \backsim \Delta MNP\) theo định nghĩa hai tam giác đồng dạng thì cần bổ sung thêm điều kiện nào?

  • A
    \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) .
  • B
    \(\frac{{AB}}{{NP}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NM}}\) .
  • C
    \(\frac{{AB}}{{MN}} = \frac{{AC}}{{NP}} = \frac{{BC}}{{MP}}\) .
  • D
    \(\frac{{AB}}{{MP}} = \frac{{AC}}{{NP}} = \frac{{BC}}{{NM}}\) .

Đáp án : A

Phương pháp giải :
Dựa vào định nghĩa hai tam giác đồng dạng
Lời giải chi tiết :

\(\Delta ABC \backsim \Delta MNP \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}}\\{\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P}\end{array}} \right.\)

Mà \(\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P(gt)\)

nên cần bổ sung thêm điều kiện \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) thì \(\Delta ABC \backsim \Delta MNP\) (định nghĩa).

Câu 4 :

Cho \(\Delta ABC \backsim \Delta MNP\) theo tỉ số 2. Khẳng định nào sau đây là đúng

  • A
    \(MN = 2{\rm{A}}B\) .
  • B
    \(AC = 2NP\) .
  • C
    \(MP = 2BC\) .
  • D
    \(BC = 2.NP\) .

Đáp án : D

Phương pháp giải :
Dựa vào định nghĩa hai tam giác đồng dạng
Lời giải chi tiết :

Vì \(\Delta ABC \backsim \Delta MNP\) theo tỉ số 2 (gt) \( \Rightarrow BC = 2NP\)

Câu 5 :

Hãy chọn câu đúng

Nếu \(\Delta ABC \backsim \Delta MNP\) theo tỉ số \(k = \frac{2}{3}\) thì \(\Delta MNP \backsim \Delta ABC\) theo tỉ số

  • A
    \(\frac{2}{3}\) .
  • B
    \(\frac{3}{2}\) .
  • C
    \(\frac{4}{9}\) .
  • D
    \(\frac{4}{3}\) .

Đáp án : B

Phương pháp giải :
Dựa vào định nghĩa hai tam giác đồng dạng
Lời giải chi tiết :

Vì \(\Delta ABC \backsim \Delta MNP\) theo tỉ số đồng dạng là \(k = \frac{2}{3}\) \( \Rightarrow \Delta MNP \backsim \Delta ABC\) theo tỉ số đồng dạng là \(\frac{1}{k} = \frac{3}{2}\)

Câu 6 :

Cho \(\Delta ABC,\Delta MNP\) biết \(AB = 3cm;AC = 4cm;BC = 5cm;MN = 6cm;MP = 8cm;NP = 10cm\) và \(\widehat A = {90^o};\widehat B = {60^o};\widehat M = {90^o};\widehat P = {30^o}\) thì:

  • A
    \(\Delta ABC \backsim \Delta PNM\) .
  • B
    \(\Delta ABC \backsim \Delta NMP\) .
  • C
    \(\Delta ABC \backsim \Delta MNP\) .
  • D
    \(\Delta ABC \backsim \Delta MPN\) .

Đáp án : C

Phương pháp giải :
Tính số đo các góc C, N và áp dụng định nghĩa hai tam giác đồng dạng.
Lời giải chi tiết :

\(\Delta ABC\) có \(\widehat C = {180^o} - \left( {\widehat A + \widehat B} \right) = {180^o} - \left( {{{90}^o} + {{80}^o}} \right) = {30^o}\) (Định lý tổng ba góc trong tam giác )

\(\Delta MNP\) có \(\widehat N = {180^o} - \left( {\widehat M + \widehat P} \right) = {180^o} - \left( {{{90}^o} + {{30}^o}} \right) = {60^o}\) (Định lý tổng ba góc trong tam giác)

Xét \(\Delta ABC\) và \(\Delta MNP\) có:

\(\frac{{AB}}{{MN}} = \frac{{18}}{6} = 3;\frac{{AC}}{{MP}} = \frac{{24}}{8} = 3;\frac{{BC}}{{NP}} = \frac{{30}}{{10}} = 3\)

\( \Rightarrow \frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\)

Vậy \(\widehat A = \widehat M\left( { = {{90}^o}} \right);\widehat B = \widehat N\left( { = {{60}^o}} \right);\widehat C = \widehat P\left( { = {{30}^o}} \right)\)

Câu 7 :

Cho \(\Delta ABC \backsim \Delta D{\rm{EF}}\) biết \(\widehat A = {50^o};\widehat B = {60^o}\) . Khi đó số đo góc D bằng

  • A
    \({50^o}\) .
  • B
    \({60^o}\) .
  • C
    \({70^o}\) .
  • D
    \({80^o}\) .

Đáp án : A

Phương pháp giải :
Dựa vào định nghĩa hai tam giác đồng dạng
Lời giải chi tiết :

Vì \(\Delta ABC \backsim \Delta D{\rm{EF}} \Rightarrow \widehat A = \widehat D\) (hai góc tương ứng)

Mà \(\widehat A = {50^o}(gt) \Rightarrow \widehat D = {50^o}\)

Câu 8 :

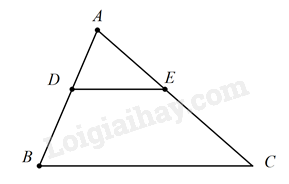
Cho tam giác ABC, trên AB lấy điểm D. Qua D kẻ đường thẳng song song với BC cắt AC ở E. Khẳng định nào sau đâyđúng

  • A
    \(\Delta ABC \backsim \Delta A{\rm{D}}E\) .
  • B
    \(\Delta ABC \backsim \Delta A{\rm{ED}}\) .
  • C
    \(\Delta BAC \backsim \Delta A{\rm{D}}E\) .
  • D
    \(\Delta ACB \backsim \Delta DE{\rm{A}}\) .

Đáp án : A

Phương pháp giải :
Sử dụng định lí của hai tam giác đồng dạng.
Lời giải chi tiết :

Vì \(DE//BC \left( {gt} \right)\Rightarrow \Delta ABC \backsim \Delta A{\rm{D}}E\)

Câu 9 :

Cho \(\Delta ABC \backsim \Delta DEF\) theo tỉ số \({k_1}\) , \(\Delta MNP \backsim \Delta D{\rm{EF}}\) theo tỉ số \({k_2}\) . Hỏi \(\Delta ABC \backsim \Delta MNP\) theo tỉ số nào ?

  • A
    \({k_1}\) .
  • B
    \(\frac{{{k_2}}}{{{k_1}}}\) .
  • C
    \(\frac{{{k_1}}}{{{k_2}}}\) .
  • D
    \({k_1}{k_2}\) .

Đáp án : C

Phương pháp giải :
Dựa vào tính chất của hai tam giác đồng dạng.
Lời giải chi tiết :

Vì \(\Delta ABC \backsim \Delta D{\rm{EF}}\) theo tỉ số \({k_1} \Rightarrow \frac{{AB}}{{DE}} = {k_1}\)

Vì \(\Delta MNP \backsim \Delta D{\rm{EF}}\) theo tỉ số \({k_2} \Rightarrow \frac{{MN}}{{DE}} = {k_2}\)

\( \Rightarrow \frac{{AB}}{{MN}} = \frac{{AB}}{{DE}}:\frac{{MN}}{{DE}} = \frac{{{k_1}}}{{{k_2}}}\)

Câu 10 :

Cho \(\Delta ABC \backsim \Delta MNP\) . Biết \(AB = 5cm;BC = 6cm;MN = 10cm;MP = 5cm\) . Hãy chọn đáp án đúng:

  • A
    \(NP = 2,5cm;AC = 12cm\)
  • B
    \(NP = 12cm;AC = 2,5cm\)
  • C
    \(NP = 5cm;AC = 10cm\)
  • D
    \(NP = 10cm;AC = 5cm\)

Đáp án : B

Phương pháp giải :
Áp dụng định nghĩa hai tam giác đồng dạng.
Lời giải chi tiết :

Vì \(\Delta ABC \backsim \Delta MNP \Rightarrow \frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) (hai cạnh tương ứng)

\(\begin{array}{l} \Rightarrow \frac{5}{{10}} = \frac{{AC}}{5} = \frac{6}{{NP}}\\ \Rightarrow AC = \frac{{5.5}}{{10}} = 2,5cm;NP = \frac{{10.6}}{5} = 12cm\end{array}\)

Câu 11 :

Cho hình vẽ, biết AB // DE. Tính tỉ số độ dài của x và y.

  • A
    18.
  • B
    \(\frac{1}{9}\) .
  • C
    2.
  • D
    \(\frac{1}{2}\) .

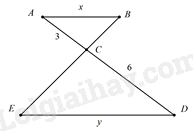
Đáp án : D

Phương pháp giải :
Áp dụng định lí của hai tam giác đồng dạng
Lời giải chi tiết :

Vì AB // DE \( \Rightarrow \Delta ABC \backsim \Delta DEC\) (định lí)

\( \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{C{\rm{D}}}}\) (các cạnh tương ứng) \( \Rightarrow \frac{x}{y} = \frac{3}{6} = \frac{1}{2}\)

Câu 12 :

Cho \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) theo tỉ số \(2:3\) và \(\Delta {A_1}{B_1}{C_1} \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số 1 :3. Vậy \(\Delta ABC \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số k bằng

  • A
    \(k = 3:9\)
  • B
    \(k = 2:9\)
  • C
    \(k = 2:6\)
  • D
    \(k = 1:3\)

Đáp án : B

Phương pháp giải :
Áp dụng tính chất của hai tam giác đồng dạng.
Lời giải chi tiết :

Vì \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) theo tỉ số \(2:3 \Rightarrow \frac{{AB}}{{{A_1}{B_1}}} = \frac{2}{3}\)

Vì \(\Delta {A_1}{B_1}{C_1} \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số \(1:3 \Rightarrow \frac{{{A_1}{B_1}}}{{{A_2}{B_2}}} = \frac{1}{3}\)

\( \Rightarrow \frac{{AB}}{{{A_2}{B_2}}} = \frac{{AB}}{{{A_1}{B_1}}}.\frac{{{A_1}{B_1}}}{{{A_2}{B_2}}} = \frac{2}{3}.\frac{1}{3} = \frac{2}{9}\)

Vậy \(\Delta ABC \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số \(k = 2:9\) .

Câu 13 :

Cho \(\Delta {A_1}{B_1}{C_1} \backsim \Delta ABC\) theo tỉ số đồng dạng \(k = \frac{2}{3}\) . Tỉ số chu vi của hai tam giác đó là:

  • A
    \(\frac{4}{9}\).
  • B
    \(\frac{3}{2}\).
  • C
    \(\frac{3}{4}\).
  • D
    \(\frac{2}{3}\).

Đáp án : D

Phương pháp giải :
Áp dụng tính chất của hai tam giác đồng dạng
Lời giải chi tiết :

Vì \(\Delta {A_1}{B_1}{C_1} \backsim \Delta ABC\) theo tỉ số đồng dạng \(k = \frac{2}{3}\) .

\(\begin{array}{l} \Rightarrow \frac{{{A_1}{B_1}}}{{AB}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{B_1}{C_1}}}{{BC}} = \frac{{{A_1}{B_1} + {A_1}{C_1} + {B_1}{C_1}}}{{AB + AC + BC}} = \frac{2}{3}\\ \Rightarrow \frac{{C{V_{\Delta {A_1}{B_1}{C_1}}}}}{{C{V_{\Delta ABC}}}} = \frac{2}{3}\end{array}\)

Hai tam giác đồng dạng theo tỉ số nào thì chu vi cũng đồng dạng theo tỉ số đó.

Câu 14 :

Cho \(\Delta MNI \backsim \Delta ABC\) theo tỉ số \(k = \frac{5}{7}\) và hiệu chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác.

  • A
    \({C_{\Delta MNI}} = 30m,{C_{\Delta ABC}} = 46m.\)
  • B
    \({C_{\Delta MNI}} = 56m,{C_{\Delta ABC}} = 40m.\)
  • C
    \({C_{\Delta MNI}} = 24m,{C_{\Delta ABC}} = 40m.\)
  • D
    \({C_{\Delta MNI}} = 40m,{C_{\Delta ABC}} = 56m.\)

Đáp án : D

Phương pháp giải :
Dựa vào hai tam giác đồng dạng tính tỉ số chu vi của hai tam giác. Từ đó tính chu vi của mỗi tam giác.
Lời giải chi tiết :

Vì \(\Delta MNI \backsim \Delta ABC\) theo tỉ số \(k = \frac{5}{7}\)

\(\begin{array}{l} \Rightarrow \frac{{MN}}{{AB}} = \frac{{MI}}{{AC}} = \frac{{NI}}{{BC}} = \frac{{MN + MI + NI}}{{AB + AC + BC}} = \frac{5}{7}\\ \Rightarrow \frac{{C{V_{\Delta MNI}}}}{{C{V_{\Delta ABC}}}} = \frac{5}{7} \Rightarrow \frac{{C{V_{\Delta MNI}}}}{{C{V_{\Delta ABC}} - C{V_{\Delta MNI}}}} = \frac{5}{{7 - 5}}\\ \Rightarrow \frac{{C{V_{\Delta MNI}}}}{{16}} = \frac{5}{2} \Rightarrow C{V_{\Delta MNI}} = \frac{{16.5}}{2} = 40(cm).\\ \Rightarrow C{V_{\Delta ABC}} = 40 + 16 = 56(cm).\end{array}\)

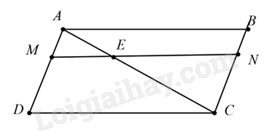
Câu 15 :

Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm E sao cho AC = 3.AE. Qua E vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:

\((I)\Delta AME \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_1} = \frac{1}{3}\)

\((II)\Delta CBA \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_2} = 1\)

\((III)\Delta CNE \backsim \Delta A{\rm{D}}C\) , tỉ số đồng dạng \({k_3} = \frac{2}{3}\)

Chọn câu đúng:

  • A
    (I) đúng, (II) và (III) sai.
  • B
    (I) và (II) đúng, (III) sai.
  • C
    (I) , (II), (III) đều đúng.
  • D
    (I), (II), (III) đều sai.

Đáp án : C

Phương pháp giải :
Sử dụng định nghĩa, tính chất của hai tam giác đồng dạng.
Lời giải chi tiết :

Xét \(\Delta A{\rm{D}}C\) có \(ME//C{\rm{D}}\) (gt) \( \Rightarrow \Delta AM{\rm{E}} \backsim \Delta A{\rm{D}}C(1)\) theo tỉ số đồng dạng \({k_1} = \frac{{A{\rm{E}}}}{{AC}} = \frac{1}{3}\)

Vì ABCD là hình bình hành nên

+ \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over D} \)

+ \(AB//C{\rm{D}} \Rightarrow \widehat {BAC} = \widehat {AC{\rm{D}}}\) (so le trong)

+ \(AD//BC \Rightarrow \widehat {ACB} = \widehat {CA{\rm{D}}}\) (so le trong)

+ AD = BC ; AB = CD

Xét \(\Delta CBA\) và \(\Delta A{\rm{D}}C\) có :

+ \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over D} ;\widehat {BAC} = \widehat {AC{\rm{D}}};\widehat {ACB} = \widehat {CA{\rm{D}}}(cmt)\)

+ \(\frac{{AB}}{{C{\rm{D}}}} = \frac{{BC}}{{A{\rm{D}}}} = \frac{{AC}}{{AC}}( = 1)\)

\( \Rightarrow \Delta CBA \backsim \Delta A{\rm{D}}C\) theo tỉ lệ đồng dạng \({k_2} = 1\)

Xét \(\Delta ABC\) có :

EN//CD (gt) mà AB//CD (cmt)

\( \Rightarrow EN//AB \Rightarrow \Delta CNE \backsim \Delta CBA\)

Mà \(\Delta CBA \backsim \Delta A{\rm{D}}C(cmt)\)

\( \Rightarrow \Delta CNE \backsim \Delta A{\rm{D}}C\) theo tỉ lệ đồng dạng \({k_3} = \frac{{CE}}{{AC}} = \frac{2}{3}\) (Vì \(AC = 3{\rm{AE}} \Rightarrow CE = \frac{2}{3}AC)\)

Vậy khẳng định (I), (II), (III) đều đúng.

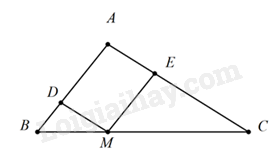
Câu 16 :

Cho tam giác ABC , lấy M trên cạnh BC sao cho \(\frac{{MB}}{{MC}} = \frac{1}{2}\) Qua M kẻ đường thẳng song song với AC cắt AB tại D và đường thẳng song song với AB cắt AD tại E biết chu vi tam giác MEC bằng 24 cm thì chu vi tam giác DBM là

  • A
    12cm .
  • B
    24 cm.
  • C
    48 cm.
  • D
    36cm .

Đáp án : A

Phương pháp giải :
Áp dụng tính chất của hai tam giác đồng dạng.
Lời giải chi tiết :

Vì MD // AC \( \Rightarrow \Delta DBM \backsim \Delta ABC\)

Vì ME // AB \( \Rightarrow \Delta EMC \backsim \Delta ABC\)

\( \Rightarrow \Delta DBM \backsim \Delta EMC\left( { \backsim \Delta ABC} \right)\)

\(\begin{array}{l} \Rightarrow \frac{{DB}}{{EM}} = \frac{{DM}}{{EC}} = \frac{{BM}}{{MC}} = \frac{{DB + DM + BM}}{{EM + EC + MC}} = \frac{1}{2}\\\frac{{C{V_{\Delta DBM}}}}{{C{V_{\Delta EMC}}}} = \frac{1}{2}\end{array}\)

Mà chu vi tam giác MEC bằng 24 cm

Chu vi tam giác DBM bằng 24 : 2 = 12 (cm).

Bài liên quan
close

Tiện ích | Blog

Nội dung từ Loigiaihay.Com