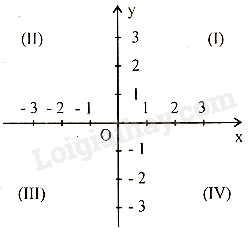Trắc nghiệm Bài 2: Tọa độ của một điểm và đồ thị của hàm số Toán 8 Chân trời sáng tạoĐề bài
Câu 1 :
Chọn khẳng định đúng.
Câu 2 :
Chọn đáp án đúng.
Câu 3 :
Cho điểm M(a; b) trong mặt phẳng tọa độ Oxy, khi đó:
Câu 4 :
Điểm thuộc trục hoành thì có tung độ bằng:
Câu 5 :
Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm M có tọa độ:
Câu 7 :
Điểm A(1;3) không thuộc đồ thị hàm số:
Câu 9 :
Trong mặt phẳng tọa độ Oxy cho điểm A nằm trên trục tung và có tung độ là 2. Điểm A’ đối xứng với điểm A qua gốc tọa độ O có tọa độ là:
Câu 10 :
Cho các cặp số (a; b) biết rằng a, b thuộc tập hợp \(\left\{ {2; - 2} \right\}\). Khi biểu diễn tất cả các cặp số này trên mặt phẳng tọa độ Oxy thì có tất cả bao nhiêu điểm thuộc góc phần tư thứ IV?
Câu 11 :
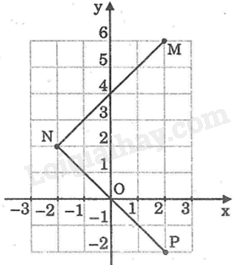
Trên mặt phẳng tọa độ Oxy, hàm số \(y = f\left( x \right)\) có đồ thị là hai đoạn thẳng OA và AB như hình vẽ dưới đây. Hàm số \(y = f\left( x \right)\) được cho bởi công thức nào?
Câu 12 :
Trên mặt phẳng tọa độ Oxy, hàm số \(y = f\left( x \right)\) có đồ thị là hai đoạn thẳng OA và AB, và đồ thị hàm số \(y = g\left( x \right) = \frac{1}{3}x\) như hình vẽ dưới đây:
Có bao nhiêu giá trị của x để \(f\left( x \right) = g\left( x \right)\)
Câu 13 :
Trong mặt phẳng tọa độ cho các điểm \(M\left( {2;3} \right),N\left( { - 2;3} \right),P\left( {2; - 3} \right);Q\left( { - 2; - 3} \right).\) Trong các đoạn thẳng MP, PQ, NQ, MN, số đoạn thẳng song song với trục hoành là:
Câu 15 :
Cho đồ thị hàm số \(y = - 3{x^2} + 1\) và điểm C thuộc đồ thị đó. Nếu tung độ của điểm C là 1 thì tọa độ của điểm C là:
Câu 16 :
Cho đồ thị hàm số \(y = 6x.\) Điểm A thuộc đồ thị hàm số đó. Biết rằng điểm A có hoành độ bằng 2. Khi đó, tọa độ của điểm A là:
Câu 17 :
Cho hàm số \(y = \left( {2m - 1} \right){x^2}.\) Biết rằng đồ thị hàm số trên đi qua điểm A(1; 1). Khi đó,
Câu 18 :
: Cho hệ trục tọa độ Oxy, diện tích của hình chữ nhật giới hạn bởi hai trục tọa độ và hai đường thẳng chứa tất cả các điểm có hoành độ bằng 3 và tất cả các điểm có tung độ bằng 2 là:
Câu 19 :
Trên mặt phẳng tọa độ Oxy, cho ba điểm A(1; 4), B(-3; -4), C(1; 0). Khi đó, diện tích tam giác ABC là:
Lời giải và đáp án
Câu 1 :
Chọn khẳng định đúng.
Đáp án : A Phương pháp giải :
Sử dụng định nghĩa hệ trục tọa độ: Trên mặt phẳng, vẽ hai trục Ox, Oy vuông góc với nhau và cắt nhau tại gốc O của mỗi trục. Khi đó, ta có hệ trục tọa độ Oxy.
Lời giải chi tiết :
Trên mặt phẳng, vẽ hai trục Ox, Oy vuông góc với nhau và cắt nhau tại gốc O của mỗi trục. Khi đó, ta có hệ trục tọa độ Oxy.
Câu 2 :
Chọn đáp án đúng.
Đáp án : C Phương pháp giải :
Hai trục tọa độ Ox, Oy chia mặt phẳng tọa độ Oxy thành bốn góc: Góc phần tư thứ I, góc phần tư thứ II, góc phần tư thứ III, góc phần tư thứ IV theo ngược chiều kim đồng hồ
Lời giải chi tiết :
Hai trục tọa độ Ox, Oy chia mặt phẳng tọa độ Oxy thành bốn góc: Góc phần tư thứ I, góc phần tư thứ II, góc phần tư thứ III, góc phần tư thứ IV theo ngược chiều kim đồng hồ
Câu 3 :
Cho điểm M(a; b) trong mặt phẳng tọa độ Oxy, khi đó:
Đáp án : D Phương pháp giải :
Sử dụng định nghĩa tọa độ của điểm trong mặt phẳng: Cho điểm M trong mặt phẳng tọa độ Oxy, giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục số Oy. Cặp số (a; b) được gọi là tọa độ của điểm M, a là hoành độ, b là tung độ của điểm M.
Lời giải chi tiết :
Cho điểm M(a; b) trong mặt phẳng tọa độ Oxy, khi đó a là hoành độ, b là tung độ của điểm M
Câu 4 :
Điểm thuộc trục hoành thì có tung độ bằng:
Đáp án : C Phương pháp giải :
Điểm thuộc trục hoành thì có tung độ bằng 0.
Lời giải chi tiết :
Điểm thuộc trục hoành thì có tung độ bằng 0.
Câu 5 :
Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm M có tọa độ:
Đáp án : A Phương pháp giải :
Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)
Lời giải chi tiết :
Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)
Đáp án : A Phương pháp giải :
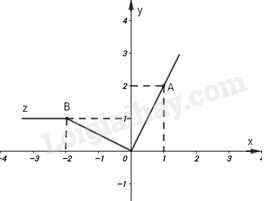
+ Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\) + Sử dụng định nghĩa tọa độ của điểm trong mặt phẳng: Cho điểm M trong mặt phẳng tọa độ Oxy, giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục số Oy. Cặp số (a; b) được gọi là tọa độ của điểm M, a là hoành độ, b là tung độ của điểm M. Lời giải chi tiết :
Từ hình vẽ ta thấy B(-2;1) và điểm A(1;2) thuộc đồ thị hàm số. Do đó, \(f\left( { - 2} \right) = 1;f\left( 1 \right) = 2\)
Câu 7 :
Điểm A(1;3) không thuộc đồ thị hàm số:
Đáp án : D Phương pháp giải :
Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)
Lời giải chi tiết :
Ta thấy: \(3 \ne {1^2}\) nên điểm A(1;3) không thuộc đồ thị hàm số \(y = {x^2}\)
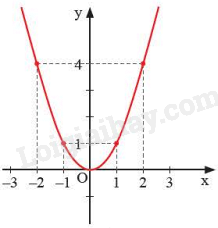
Đáp án : C Phương pháp giải :
+ Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\) + Sử dụng định nghĩa tọa độ của điểm trong mặt phẳng: Cho điểm M trong mặt phẳng tọa độ Oxy, giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục số Oy. Cặp số (a; b) được gọi là tọa độ của điểm M, a là hoành độ, b là tung độ của điểm M. Lời giải chi tiết :
Nhìn vào đồ thị trong hình vẽ ta thấy, \(x = 1\) thì \(y = 1\) Vậy điểm có tọa độ (1; 1) thuộc đồ thị hàm số.
Câu 9 :
Trong mặt phẳng tọa độ Oxy cho điểm A nằm trên trục tung và có tung độ là 2. Điểm A’ đối xứng với điểm A qua gốc tọa độ O có tọa độ là:
Đáp án : D Phương pháp giải :
Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)
Lời giải chi tiết :
Vì điểm A nằm trên trục tung và có tung độ bằng 2 nên A(0; 2) Điểm A’ đối xứng với điểm A qua gốc tọa độ O nên O là trung điểm của đoạn thẳng AA’. Do đó, A’ thuộc trục tung và có tung độ là \( - 2\) Vậy A’(0; -2)
Câu 10 :
Cho các cặp số (a; b) biết rằng a, b thuộc tập hợp \(\left\{ {2; - 2} \right\}\). Khi biểu diễn tất cả các cặp số này trên mặt phẳng tọa độ Oxy thì có tất cả bao nhiêu điểm thuộc góc phần tư thứ IV?
Đáp án : A Phương pháp giải :
Hai trục tọa độ Ox, Oy chia mặt phẳng tọa độ Oxy thành bốn góc: Góc phần tư thứ I, góc phần tư thứ II, góc phần tư thứ III, góc phần tư thứ IV theo ngược chiều kim đồng hồ
Lời giải chi tiết :
Có 4 cặp số được biểu diễn bởi các điểm: A(2; 2), B(2; -2), C(-2; 2), D(-2; -2) Trong các điểm trên, chỉ có 1 điểm thuộc góc phần tư thứ IV là: B(2; -2)
Câu 11 :
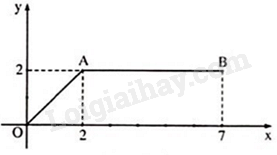
Trên mặt phẳng tọa độ Oxy, hàm số \(y = f\left( x \right)\) có đồ thị là hai đoạn thẳng OA và AB như hình vẽ dưới đây. Hàm số \(y = f\left( x \right)\) được cho bởi công thức nào?
Đáp án : C Phương pháp giải :
Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)
Lời giải chi tiết :
Nhìn vào đồ thị ta thấy: Với \(2 < x \le 7\) ta thấy đồ thị hàm số là đường thẳng \(y = 2\) Với \(0 \le x \le 2\) ta thấy đồ thị hàm số là đường thẳng \(y = x\) Vậy \(y = \left\{ \begin{array}{l}x\;\;khi\;\;0 \le x \le 2\\2\;\;khi\;\;2 < x \le 7\end{array} \right.\)
Câu 12 :
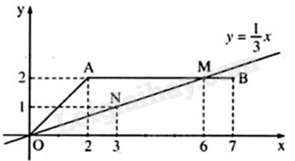
Trên mặt phẳng tọa độ Oxy, hàm số \(y = f\left( x \right)\) có đồ thị là hai đoạn thẳng OA và AB, và đồ thị hàm số \(y = g\left( x \right) = \frac{1}{3}x\) như hình vẽ dưới đây:
Có bao nhiêu giá trị của x để \(f\left( x \right) = g\left( x \right)\)
Đáp án : C Phương pháp giải :
Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)
Lời giải chi tiết :
Đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại điểm O(0;0) và M(6;2) Với \(x = 0\) thì \(f\left( x \right) = g\left( x \right) = 0\) Với \(x = 6\) thì \(f\left( x \right) = g\left( x \right) = 2\) Do đó, có 2 giá trị của x để \(f\left( x \right) = g\left( x \right)\)
Câu 13 :
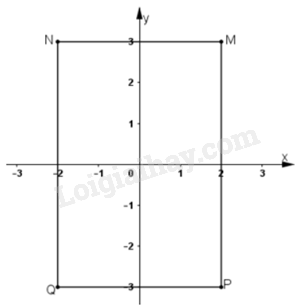
Trong mặt phẳng tọa độ cho các điểm \(M\left( {2;3} \right),N\left( { - 2;3} \right),P\left( {2; - 3} \right);Q\left( { - 2; - 3} \right).\) Trong các đoạn thẳng MP, PQ, NQ, MN, số đoạn thẳng song song với trục hoành là:
Đáp án : B Phương pháp giải :
Sử dụng định nghĩa tọa độ của điểm trong mặt phẳng: Cho điểm M trong mặt phẳng tọa độ Oxy, giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục số Oy. Cặp số (a; b) được gọi là tọa độ của điểm M, a là hoành độ, b là tung độ của điểm M
Lời giải chi tiết :
Biểu diễn các điểm \(M\left( {2;3} \right),N\left( { - 2;3} \right),P\left( {2; - 3} \right);Q\left( { - 2; - 3} \right)\) trên mặt phẳng tọa độ
Nhìn vào đồ thị ta thấy đoạn thẳng song song với trục hoành là MN và PQ.
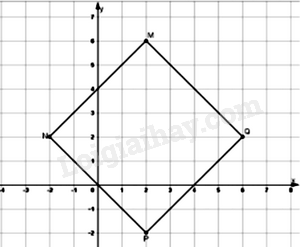
Đáp án : D Phương pháp giải :
Sử dụng định nghĩa tọa độ của điểm trong mặt phẳng: Cho điểm M trong mặt phẳng tọa độ Oxy, giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục số Oy. Cặp số (a; b) được gọi là tọa độ của điểm M, a là hoành độ, b là tung độ của điểm M
Lời giải chi tiết :
Điểm P cách điểm N là 4 ô chéo thì điểm Q cũng cách điểm M 4 ô chéo Điểm N cách trục hoành 2 ô vuông thì điểm Q cách trục hoành 2 ô vuông. Do đó, điểm Q(6; 2)
Câu 15 :
Cho đồ thị hàm số \(y = - 3{x^2} + 1\) và điểm C thuộc đồ thị đó. Nếu tung độ của điểm C là 1 thì tọa độ của điểm C là:
Đáp án : C Phương pháp giải :
Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)
Lời giải chi tiết :
Vì tung độ của điểm C là 1 nên \(y = 1\). Thay \(y = 1\) vào \(y = - 3{x^2} + 1\) ta có: \(1 = - 3{x^2} + 1\) \(0 = - 3{x^2}\) \(x = 0\) Vậy \(C\left( {0;1} \right)\)
Câu 16 :
Cho đồ thị hàm số \(y = 6x.\) Điểm A thuộc đồ thị hàm số đó. Biết rằng điểm A có hoành độ bằng 2. Khi đó, tọa độ của điểm A là:
Đáp án : D Phương pháp giải :
Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)
Lời giải chi tiết :
Điểm A có hoành độ bằng 2 nên \(x = 2.\) Thay \(x = 2\) vào \(y = 6x\) ta có: \(y = 2.6 = 12\) Vậy A(2; 12)
Câu 17 :
Cho hàm số \(y = \left( {2m - 1} \right){x^2}.\) Biết rằng đồ thị hàm số trên đi qua điểm A(1; 1). Khi đó,
Đáp án : C Phương pháp giải :
Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\)
Lời giải chi tiết :
Vì đồ thị hàm số đã cho đi qua A(1; 1) nên \(x = 1;y = 1.\) Thay vào hàm số ta có: \(1 = \left( {2m - 1} \right){.1^2}\) \(1 = 2m - 1\) \(2m = 2\) \(m = 1\) Vậy với \(m = 1\) thì thỏa mãn yêu cầu bài toán
Câu 18 :
: Cho hệ trục tọa độ Oxy, diện tích của hình chữ nhật giới hạn bởi hai trục tọa độ và hai đường thẳng chứa tất cả các điểm có hoành độ bằng 3 và tất cả các điểm có tung độ bằng 2 là:
Đáp án : C Phương pháp giải :
Sử dụng định nghĩa tọa độ của điểm trong mặt phẳng: Cho điểm M trong mặt phẳng tọa độ Oxy, giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục số Oy. Cặp số (a; b) được gọi là tọa độ của điểm M, a là hoành độ, b là tung độ của điểm M
+ Sử dụng khái niệm đồ thị của hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm \(M\left( {x;f\left( x \right)} \right)\) Lời giải chi tiết :
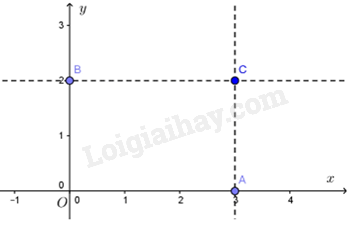
Các điểm có hoành độ bằng 3 nằm trên đường thẳng song song với trục tung và cắt trục hoành tại điểm có hoành độ bằng 3. Các điểm có tung độ bằng 2 nằm trên đường thẳng song song với trục hoành và cắt trục tung tại điểm có tung độ bằng 2. Do đó, ta có đồ thị hàm số:
Gọi tên các giao điểm như hình vẽ, ta được hình chữ nhật OBCA. Do đó, diện tích hình chữ nhật OBCA là: \({S_{OBCA}} = OA.OB = 3.2 = 6\) (đvdt)
Câu 19 :
Trên mặt phẳng tọa độ Oxy, cho ba điểm A(1; 4), B(-3; -4), C(1; 0). Khi đó, diện tích tam giác ABC là:
Đáp án : B Phương pháp giải :
Sử dụng định nghĩa tọa độ của điểm trong mặt phẳng: Cho điểm M trong mặt phẳng tọa độ Oxy, giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục số Oy. Cặp số (a; b) được gọi là tọa độ của điểm M, a là hoành độ, b là tung độ của điểm M
Lời giải chi tiết :
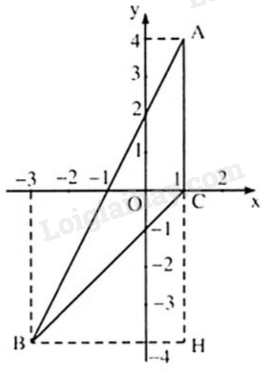
Biểu diễn các điểm A, B, C trên mặt phẳng tọa độ Oxy ta được:
Kẻ BH vuông góc với AC, khi đó, BH là đường cao trong tam giác ABC. Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}BH.AC = \frac{1}{2}.4.4 = 8\) (đvdt)
|