Cho $\Delta ABC \backsim \Delta MNP$ . Biết $AB = 5cm;BC = 6cm;MN = 10cm;MP = 5cm$ . Hãy chọn đáp án đúng:

Hãy chọn câu đúng.

Hãy chọn câu sai.

Cho $\Delta ABC,\Delta MNP$ nếu có $\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P$ để $\Delta ABC \backsim \Delta MNP$ theo định nghĩa hai tam giác đồng dạng thì cần bổ sung thêm điều kiện nào?

Cho $\Delta ABC \backsim \Delta MNP$ theo tỉ số 2. Khẳng định nào sau đây là đúng

Hãy chọn câu đúng

Nếu $\Delta ABC \backsim \Delta MNP$ theo tỉ số $k = \frac{2}{3}$ thì $\Delta MNP \backsim \Delta ABC$ theo tỉ số

Cho $\Delta ABC,\Delta MNP$ biết $AB = 3cm;AC = 4cm;BC = 5cm;MN = 6cm;MP = 8cm;NP = 10cm$ và $\widehat A = {90^o};\widehat B = {60^o};\widehat M = {90^o};\widehat P = {30^o}$ thì:

Cho $\Delta ABC \backsim \Delta D{\rm{EF}}$ biết $\widehat A = {50^o};\widehat B = {60^o}$ . Khi đó số đo góc D bằng

Cho tam giác ABC, trên AB lấy điểm D. Qua D kẻ đường thẳng song song với BC cắt AC ở E. Khẳng định nào sau đâyđúng

Cho $\Delta ABC \backsim \Delta DEF$ theo tỉ số ${k_1}$ , $\Delta MNP \backsim \Delta D{\rm{EF}}$ theo tỉ số ${k_2}$ . Hỏi $\Delta ABC \backsim \Delta MNP$ theo tỉ số nào ?

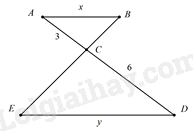
Cho hình vẽ, biết AB // DE. Tính tỉ số độ dài của x và y.

Cho $\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}$ theo tỉ số $2:3$ và $\Delta {A_1}{B_1}{C_1} \backsim \Delta {A_2}{B_2}{C_2}$ theo tỉ số 1 :3. Vậy $\Delta ABC \backsim \Delta {A_2}{B_2}{C_2}$ theo tỉ số k bằng

Cho $\Delta {A_1}{B_1}{C_1} \backsim \Delta ABC$ theo tỉ số đồng dạng $k = \frac{2}{3}$ . Tỉ số chu vi của hai tam giác đó là:

Cho $\Delta MNI \backsim \Delta ABC$ theo tỉ số $k = \frac{5}{7}$ và hiệu chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác.

Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm E sao cho AC = 3.AE. Qua E vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:

$(I)\Delta AME \backsim \Delta A{\rm{D}}C$ , tỉ số đồng dạng ${k_1} = \frac{1}{3}$

$(II)\Delta CBA \backsim \Delta A{\rm{D}}C$ , tỉ số đồng dạng ${k_2} = 1$

$(III)\Delta CNE \backsim \Delta A{\rm{D}}C$ , tỉ số đồng dạng ${k_3} = \frac{2}{3}$

Chọn câu đúng:

Cho tam giác ABC, lấy M trên cạnh BC sao cho $\frac{{MB}}{{MC}} = \frac{1}{2}$. Qua M kẻ đường thẳng song song với AC cắt AB tại D và đường thẳng song song với AB cắt AD tại E biết chu vi tam giác MEC bằng 24 cm thì chu vi tam giác DBM là